Серия сообщений "Сказки":
Часть 1 - Истинная правда о том, как прогнали разбойника.

В давние времена густых лесов в нашем мире было больше, так что они покрывали большую часть материка. Тогда не было могущественных империй, а существовало множество небольших государств, а также совсем мелких княжеств. Но волшебство и в те времена имело очень большую силу. Вот тогда и жил один великий волшебник. Он обладал нелюдимым характером и терпеть не мог толп вокруг себя. Больше всего он любил исследовать магию и составлять новые заклинания. Маги знают, что это очень и очень непросто, требует времени, терпения и огромного сосредоточения. Поэтому волшебник ненавидел когда его отвлекают от работы. Но как объяснить какому-нибудь просителю, особенно если он богат или облечён властью чтобы он шел со своими просьбами подальше? Волшебник выбрал подходящее место в густом труднопроходимом лесу и выстроил там небольшой, но хорошо укреплённый замок. Замок, впрочем, располагался не слишком далеко от столичного города, но к нему вела столь запутанная и зачарованная дорога, что найти его было очень сложно. Кроме самого волшебника там не было ни одного человека, всё в замке делалось с помощью волшебства. Как бы сама собой осуществлялась уборка, стирка и даже готовка пищи. Запасы продуктов на много лет вперёд волшебник сделал в подвале замка, а дальше только настроил бытовые и охранные заклинания, чтобы ничто не отвлекало его от любимого дела. У замка была даже конюшня, но чтобы не отвлекаться на уход за лошадьми, ведь это живые существа и просто накормить их недостаточно! К тому же лошади стареют, а требуются они редко. Зачем же тратить лошадиную жизнь впустую! Да и вообще - это сколько надо настроить заклинаний для простого ухода за лошадью! Поэтому волшебник поступил проще - он притормозил время в конюшне, да так сильно что казалось что оно стоит. После лошадей стоит, наверное, упомянуть про женщин, хоть это и забавно. Дело в том, что волшебник не был женононенависником, а был обыкновенным сумасшедшим учёным. Все его мысли, силы, время были посвящены магии. Так что о женщинах он вспоминал очень редко, а когда вспоминал - извлекал из замедленного времени лошадку и ехал в город, оставляя замок и вовсе безлюдным.
В первые годы, впрочем, находились ловкачи пробиравшиеся к замку и пытавшиеся выпросить у волшебника магические услуги.И откуда только узнали о местонахождении замка? Они нанимали охотников - следопытов а то и целые отряды наёмников, но ни одна попытка не окончилась удачей. Всех "счастливчиков" волшебник превращал в мышей, зайцев и других зверьков. К счастью, не навсегда. Как только они в страхе убегали от замка подальше человеческий облик к ним возвращался. Постепенно об замке стали ходить столь зловещие слухи, что желающих наведаться в "гости" больше было не сыскать. Можно было бы удивиться - зачем волшебнику потребовалось возводить свой замок рядом со столицей. А потом городить запутанные дороги. Дело в том, что иногда для проверки заклинаний ему требовались люди. И близость города облегчала эту задачу. Но волшебник не мог просто пойти в город и наловить нищих или купить рабов на рабском рынке, хотя по силе это было бы ему раз плюнуть. Дело в том, что в магии существует закон, который называют по разному, но чаще всего законом равновесия. А заключается он в том, что зло которое ты делаешь, обязательно вернётся к тебе. Кстати, закон этот существует не только для магии, просто обыкновенные люди либо не догадываются о его существовании, либо не придают значения. Многие, когда впервые узнают об этом законе, удивляются. Откуда же тогда берутся злые волшебники, да и вообще зло? Дело в том, что для простых людей наказание не бывает сильным и часто отложено на следущую жизнь. А вот для волшебников... Лучше вам об этом не знать! А злые волшебники ищут и иногда находят лазейки и обходные пути. Но наказание для них всё равно будет. Наш волшебник, разумеется, не был злым. Но и добрым назвать его трудно... Закон, конечно, он чтил и не собирался нарушать. Поэтому, если ему требовалось испытать на человеке новое заклинание он поступал так: ехал в город и искал отчаявшихся людей, таких, которым жизнь уже была не мила и заключал с ними магический контракт. В нём человек обязывался добровольно пройти испытание, и если оставался жив, то волшебник обещал исполнить желание или решить проблему, в чём бы она не заключалась. Только в этом случае волшебника не настигла бы кара за причинённое зло! Как правило, найти добровольцев было легко, ведь людей всегда преследуют беды, болезни и прочая гадость.
Но в тот раз, о котором эта история, волшебнику не очень повезло. Ему для проверки нового заклинания понадобилось не менее трех испытуемых. Первого добровольца он нашёл быстро. Это был кузнец, потерявший правую руку. Для известного мастера, которым являлся в прошлом кузнец, это была не просто трагедия. Это был конец жизни и он пропивал её остатки в третьесортном кабаке. Кузнец мгновенно согласился на контракт условием которого было отращивание новой руки. Второго добровольца пришлось поискать. Наконец, волшебник нашёл отчаявшегося молодого купца. В прошлом купец был очень успешен, торговля приносила ему хорошие прибыли, он удачно и по любви женился на красивой девушке. А когда у них с женой родился здоровый крепкий мальчик - будущий наследник, всё пошло наперекосяк. Кто-то стал строить козни, мешать осуществлять сделки, но когда у купца украли младенца он совсем потерял голову. Жена слегла от потрясения и неизвестно выживет ли. Купец сразу согласился на испытание и просил найти мальчика и вылечить жену. Но вот с третьим добровольцем долго не везло. Конечно, несчастливые люди попадались во множестве, но здесь требовался человек уже не ценивший свою жизнь. Дело шло к вечеру и волшебник уже подумывал обойтись двумя добровольцами и возвращаться в замок, как наконец-то почувствовал отчаяние исходящее от реки. Подъехав к берегу он увидел девушку, сидящюю на камне. Скорчившись она плакала и было видно что вот-вот собирается броситься в реку. Волшебнику даже пришлось применить успокаивающее заклинание, по другому говорить девушка отказывалась. Рассмотрев её внимательней он увидел что девушка некрасива, хотя уродиной назвать её тоже нельзя. Несмотря на благородное происхождение - девушка явно была дворянкой, вряд ли с такой внешностью у неё был хоть один поклонник. Она рассказала свою историю. Отец у девушки был военным и служил у здешнего короля. Когда он вышел в отставку король пожаловал ему дом с большим участком, он женился и у них родилась дочь. Назвали её Инелла - эта и была та самая отчаявшаяся девушка. Она была в семье единственным ребёнком и отец её очень любил. А вот мать... Не то чтобы она не любила свою дочь, но увидев что красавицы из неё не вырастет, как-то охладела к ней. Всему, что необходимо знать молодой дворянке мать её обучила, однако никакой теплоты между матерью и дочерью не было. Но девушка не чувствовала себя несчастной ведь её жизнь была очень насыщенной и интересной. Отец научил Инеллу не только прекрасно ездить на лошадях, ухаживать за ними но и стрелять из лука, для чего заказал для неё специальный лук. Кроме того, он часто брал дочь с собой на охоту , где обучил её разным охотничьим уловкам, обустраивать место привала, разводить костёр и готовить пищу на нем. Мать не одобряла этих уроков но не говорила ни слова против. А ещё у отца была богатая библиотека и Инелла рано научилась и полюбила читать. И вообще, нрав у неё был весёлый и незлобливый. Конечно, когда Инелла подросла и из девочки превратилась в молодую девушку, она поняла что некрасива, но не слишком переживала по этому поводу. И вот недавно к ним в гости приехал молодой человек. Это был сын сослуживца и друга отца и приехал он по каким-то делам. Молодой человек был очень хорош собой и конечно юное и неопытное сердечко Инеллы дрогнуло. Проще говоря, она без памяти влюбилась. Но Инелла была умна и понимала что такой красавец не может ею заинтересоваться. Каково же было её изумление когда парень стал не просто оказывать ей знаки внимания а настойчиво ухаживать за ней. Инелла сначала не поверила, но молодой человек был настойчив и ему удалось доказать что он влюблён. Можете себе представить счастье молодой девочки? Когда ему пришло время возвращаться он сказал Инелле, что просит стать его женой. Что он съездит домой попросит благословение у отца, а затем вернётся и они поженятся. И уехал. Инелла пребывала в каком то блаженном состоянии, ей казалось сто она летает. Она ждала что вот-вот возлюбленный приедет! Да! Три дня назад он приехал... с красавицей женой. С Инеллой он разговаривал вежливо, доброжелательно, но ни взглядом ни словом не обмолвился о том, что говорил Инелле раньше. Девушка не сразу пришла в отчаяние. Она всётаки думала что он как то объяснит свой поступок. Ну разлюбил, повстречал другую, тем более такую красавицу. "Я ведь некрасива" - думала Инелла, но обьяснить то он ведь мог? Кроме того что-то в облике и поведении возлюбленного смущало её, но что - она не могла понять. Тогда она попыталась с ним поговорить, но он сделал вид что не понимает о чём речь.Тут ещё в комнату ворвалась его жена и стала обвинять Инеллу в попытке совратить её мужа. Она наговорила таких гадостей, что бедная девушка не выдержала. Потрясение было слишком велико. Инелла ушла из дома и вот уже несколько часов сидела на берегу реки. Она действительно собиралась броситься в воду. "Не стоит делать этого" - сказал волшебник. Далее он рассказал про магический контракт и пообещал сделать Инеллу самой красивой девушкой королевства. "Подумай об отце" - сказал волшебник. И Инелла согласилась.
Волшебник привез всех троих в замок и разместил в специальных "гостевых" комнатах. К испытанию заклинания всё было готово и оно прошло успешно. Все трое выжили, чем очень обрадовали волшебника, ведь так бывало не всегда. И не только смерть испытуемого огорчала. Это ведь означало что заклинание несовершенно и его требуется доработать. Исполняя свою часть магической клятвы волшебник отрастил кузнецу руку, вернул здоровье и даже добавил ему физической силы. Иногда он на радостях делал немного больше чем обещал по контракту. Купцу он рассказал где прячут его ребёнка, дал защитные амулеты чтобы беспрепятственно вернуть мальчика и лечебное зелье для исцеления жены. А также подарил кольцо дарующее удачу в торговле. Когда купец спросил отчего это всё случилось, волшебник показал ему в магическом зеркале виновника. И купец не удержался от крика. Это оказался его лучший друг и напарник по купеческим делам. "Почему?"- закричал ошарашенный купец. "Это просто зависть" - сказал волшебник."Он во всём и всегда завидовал тебе. Когда у тебя родился сын он совсем озверел. Ведь у него не может быть детей, даже магия не может это исправить. Он хотел довести тебя до самоубийства, завладеть твоим имуществом, а твоего сына выдать за своего и вырастить как своего наследника. Но ты с ним разберёшься". А вот с девушкой... Волшебник не просто сделал её очень красивой он придал ей такое магическое очарование, что ни один мужчина не мог устоять. От этого была только одна защита - если мужчина уже был влюблён в другую. Возможно, волшебник хотел таким образом помочь Инелле найти своё счастье. Но вот что из этого получилось... Правда, проявилось это не сразу. Исполнив свою часть контракта волшебник вернул всех троих в город.
Когда Инелла вернулась домой, вызвав этим изрядный переполох, отец бросился к ней, обнял и долго не мог сказать ни слова от счастья. Оказалось что её разыскивали по всему городу и окрестностям нанятые отцом люди. Когда Инелла поинтересовалась о госте с его женой отец сказал что они собрались и уехали в тот же вечер как она пропала. Все попытки расспросить что же с ней случилось и где она была ни к чему не привели. Инелла молчала. Нет, волшебник не запретил рассказывать, но ей самой не хотелось вспоминать ни о чём. Интересно, что отец и внимания не обратил на необыкновенную красоту дочери, для него она ничуть не изменилась и осталась той же любимой дочкой. Мать же заметила изменения. Возможно, она и удивилась, но как обычно, промолчала. Несколько дней всё шло как и раньше а потом вдруг Инелла обнаружила что ей невозможно выйти на улицу. Все встречные мужчины пялились на неё. И это бы ещё ничего, но находилось немало таких, что увязывались за ней, говорили комплименты, признавались в любви и даже с ходу предлагали выйти за них замуж. Ну да, поначалу это даже забавляло, а потом стало раздражать. Кончилось всё тем, что Инелла очень редко стала покидать дом и выходить на улицу. Она сшила себе несколько очень скромных платьев из серой неяркой ткани, платья эти были лишены вообще любых украшений, вышивок, но помогало это мало. Тогда Инелла стала носить поверх этих маскировочных платьев и длинный плащ с глубоким капюшоном. Вот это немного исправило ситуацию, ей удавалось в таком виде пройти по улице не привлекая пристального внимания. А вообще она уже иногда жалела что стала такой красивой. Как же легко ей жилось раньше! Никаких же проблем! И только выходя на охоту с отцом она отдыхала душой.
Тем временем жизнь в королевстве и мире продолжалась своим чередом. У соседнего государства сменился правитель. Старый король скоропостижно скончался от болезни и даже сильные волшебники не смогли его спасти. На трон взошёл молодой и пока не женатый принц. Надо сказать, что с этим государством были на удивление очень хорошие, дружественные отношения. И молодой король решил приехать с визитом. Странного в этом ничего не было, поговаривали что он подыскивает себе невесту, ведь король обязан быть женат. А у здешнего правителя было две дочери и старшая из принцесс вполне подходила по возрасту. Надо сказать что приезд соседнего короля вызвал большой интерес у жителей столицы. Ведь по обычаю молодой король должен был проехать с кортежем по главной улице города. И горожане, разумеется, собирались поглазеть на это. Когда ещё удастся вот так в живую увидеть короля!!! Инелла тоже поддалась общему настроению. Она, как и все девицы, была любопытна. Ну, если уж совсем честно, то молодой неженатый король не мог не вызвать интерес у юной девушки. Мать попыталась предостеречь её. "Ведь там будет толпа. А если какой нибудь парень опять привяжется к тебе?" - спросила мать. "Вот именно толпа!" - воскликнула Инелла. " Всем будет не до меня! Все будут смотреть на кортеж, а я спокойно постою в своём плаще. Никто даже голову не повернёт в мою сторону!" И Инелле удалось уговорить мать отпустить её на это зрелище. Чудесно! Она надела свой "маскировочный" наряд и пошла в сторону главной улицы. Инелле повезло. Ей удалось пробраться в первый ряд плотной толпы горожан, выстроившихся в ряды с обеих сторон на всём протяжении центральной улицы столицы, ведущей ко дворцу. Ждать пришлось довольно долго. Но вот наконец по толпе пробежал восторженный ропот - "Едут! Едут!" Вдалеке показался кортеж молодого короля, а сам он ехал впереди на изящном вороном жеребце. И вот то что случилось дальше... Это было странно и настолько похоже на сказку, что объяснить можно только вмешательством волшебства! Когда жеребец короля поравнялся с местом где стояла Инелла, вдруг налетел резкий порыв ветра и сдул капюшон с её головы. А король как раз смотрел в сторону, где стояла девушка. Он придержал коня столь резко, что поднял его на дыбы, а затем, нарушая все и всяческие протоколы встречи, соскочил на землю. Впоследствии он признался, что почувствовал нечто вроде удара по голове и взрыва в сердце. Почти не соображая что делает, он подошёл к Инелле протянул ей руку и пригласил поехать с ним. Инелле тоже очень понравился юноша, пусть он хоть трижды король, неважно! И она не раздумывая ни секунды, согласилась. Вся свита короля, да и не только свита, все горожане, что видели эту сцену замерли в ступоре. Король же не обращая ни на кого внимания, как будто он был один в городе, посадил Инеллу перед собой на коня и продолжил путь в сторону дворца. "Меня зовут Коррел, я король, выходи за меня замуж и будь моей королевой!" - произнёс король. Ну, я думаю, все уже сразу догадались что ответила Инелла, и не надо это описывать. Свадьбу сыграли дважды - сначала в родном королевстве Инеллы, а потом в столице Коррела. Конечно, на свадьбу были приглашены родители девушки, и как радовался её отец! Хотя надо признать, что молодому королю пришлось преодолеть множество препон, которые возникли на пути столь скоропалительной женитьбы. Событие это породило огромное количество разных слухов, сплетен и пересудов. Чего только не говорили!
Подданные Коррела сразу полюбили свою королеву. И произошло это не только благодаря её красоте. Людям понравился её лёгкий характер, ум, добрый нрав и те дела которые королева старалась сделать для своих подданных. Впоследствии времена правления Коррела и Инеллы вошли в легенды и предания королевства как счастливое и благополучное время. У королевской четы родилось трое детей - сын наследник и две красавицы дочери. Принцессы полностью унаследовали красоту матери и к счастью, без магической привлекательности. Династия Коррела и в дальнейшем удачно правила своим государством.
Эпилог
Ну, вроде бы "Хеппи Энд"? Но нет! Не все ружья, развешенные по стенам выстрелили. То есть не всё было в этой истории объяснено. Очень странная женитьба возлюбленного Инеллы, обещавшего жениться на девушке, его мерзкое поведение, вот что это было? На самом деле со своей женой приезжал к отцу Инеллы не сам неверный жених, а его брат - близнец. Недаром Инелла чувствовала что-то странное связанное с ним. У сослуживца отца было двое сыновей - близнецов и внешне они были так похожи, что различить их могла только родная мать. Один из братьев женился на красотке и был вполне счастлив в браке. А вот второй всё никак не мог нагуляться. Он менял одну любовницу за другой. Когда отец попросил его съездить в столицу к своему другу и решить кое какие дела, он как раз разругался с очередной своей любовницей. В сердцах он поклялся ей, что жениться на любой дурнушке, так как красотки его не ценят! Когда он увидел Инеллу в сердце его бродила злость - решил выполнить свою клятву и начал ухаживать за ней. Негодник даже не подумал о чувствах девушки, тем более он и вправду хотел осуществить угрозу, в запале высказанную любовнице. Но, вернувшись домой, он неожиданно помирился с красоткой и напрочь забыл какую-то там дурнушку Инеллу. Когда отец еще раз попросил съездить в столицу тут он и призадумался. Конечно, он не собирался женится на страшилке. У него и от красоток отбоя не было. Но всё же дочь друга отца... И он не придумал ничего лучше как попросил брата съездить в столицу вместо него, да с женой. Выдать себя за него и вести себя так, будто ничего не произошло "Ничего!" - подумал он - "Увидит что я женился, поплачет и забудет меня. И отец найдёт ей в мужья какого-нибудь небрезгливого дворянчика". И брат по дурости согласился. И ведь вправду по дурости! Помните о законе равновесия? Закон этот не придуман людьми, он природный, поэтому для братьев осуществилось возмездие. Обманщик так и не смог жениться ни на одной женщине, будь она хоть дворянка, хоть простолюдинка. Даже вдовы с детьми не не хотели выходить за него, несмотря на его красоту, богатство и положение в обществе. Иногда он заводил отношения с какой-нибудь женщиной и даже получал согласие выйти за него замуж, а потом всё необъяснимым образом расстраивалось. А его брат вроде бы отделался легким испугом. По крайней мере так казалось поначалу. У него с его красавицей - женой родилось пятеро детей. Дети росли красивыми, умненькими и послушными. Но когда они вошли в возраст совершеннолетия все они, один за другим заявили отцу что не хотят его знать и покинули семью став жить самостоятельно. Ни на какие вопросы они не отвечали. У всех пятерых судьба сложилась более - менее благополучно, но до конца жизни они так и не наладили отношений ни с отцом ни с матерью. Вот справедливо ли поступил закон равновесия с братьями? Ну не знаю! Обманщик-то точно получил по заслугам!
А что же волшебник, с которого и началась эта история? Волшебники живут долго, очень долго, намного дольше обычных людей. И наш волшебник спокойно продолжал себе проживать в своём замке, составлял новые заклинания исследовал магию и был вполне счастлив. Он завёл книгу заклинаний в которую записывал результаты своих исследований. Особенностью этого гримуара было то, что не только украсть, но даже просто увидеть книгу не мог никто, только сам волшебник. И такая идиллия продолжалась довольно долго. Но вот однажды у стен замка появилось трое. Да уж! Вот этих пришельцев волшебник при всём желании не смог бы превратить в каких-нибудь зверьков! Потому что это были очень сильные волшебники из ковена магов. Конечно, он пригласил всех троих к себе в замок, хотя их появление его не порадовало. И, гости сразу "наехали" на хозяина. Сам глава ковена, пришедший по душу затворника - исследователя предъявил ему претензию: где его ученики и почему он не выполняет устав ковена и не воспитывает молодых магов? Ну да, ну да! Был такой пункт в уставе. Он очень пафосно гласил: "Магия не должна прекратиться! Каждый да воспитает не менее троих адептов, иначе магия умрёт!" Конечно, наш нелюдим знал про этот пункт. Но вот выполнять его... Вот наверно, он надеялся как-то проскочить мимо, это ведь не закон равновесия! Сердитый глава ковена поставил ультиматум: или он немедленно находит себе первого ученика или будет собран весь ковен и его лишат волшебной силы, хоть это очень трудно! Вообще-то лишение волшебной силы - это уж из ряда вон! Вряд ли ковен проголосовал бы за такую меру, ведь никакого жуткого преступления совершено не было. Но затворник был изрядно напуган, живя в отрыве от других волшебников, да и вообще от людей, он стал несколько неадекватно воспринимать действительность, пребывая в своём исследовательском мире. Он поклялся найти учеников и гости, удовлетворившись клятвой, покинули его. Клятву пришлось выполнять. Проехавшись по всему королевству волшебник отыскал троих детей со способностями к магии. А троих потому что он решил отделаться от навязанного наставничества сразу. Но наверное, чудеса случаются и в магии, как бы странно это ни звучало. Потому что ему неожиданно понравилось учительствовать, и он полюбил троих своих сорванцов - учеников. Когда его воспитанники стали полноценными магами, он нашёл следующую тройку, а потом ещё и ещё. До конца своей очень долгой жизни он учил новых адептов и не только обучал их известным заклинаниям, но и приохотил к своей любимой исследовательской работе. Многие его ученики прославились как великие маги, некоторые продолжили исследования. Может именно поэтому магия жива до сих пор, а?

Сон первый
"Хочешь, я покажу тебе кое что из моих открытий?" - Спросил Математик, вопросительно глядя на меня. "Ты ведь тоже не чужд нашей великой науке!"
Он вынул из папки лист бумаги, покрытый каким-то узором, и протянул мне. Первое мгновение я не увидел ничего необычного, но приглядевшись - ахнул! Узор представлял собой сплошь, без зазоров и перекрытий заполненную плоскость, составленную из правильных семиугольников. Я потряс головой и вопросительно посмотел на Математика. "Ну проверь. Можешь по старинке" - усмехнулся он, протягивая мне транспортир. Я долго мерил углы, хотя и так видел, что занятие это бессмысленное. Но это невозможно!
"Это ещё что!" сказал Математик с усмешкой наблюдая за мной, и подсунул мне следующий лист. На нём тоже был узор, составленный из правильных геометрических фигур, но на этот раз из восьмиугольников. Они лежали идеальными рядами, сторона к стороне, как бы издеваясь надо мной, и смотреть на них было страшно. Математик вынул ещё несколько листов, но я, чувствуя что это выше моих сил, покачал головой и взял только один. На нём тоже был узор из правильных пятиугольников красивым паркетом покрывающим лист, тоже, конечно без зазоров!!! Я нервно засмеялся и не стал проверять углы. И так было видно, что все они равны и что такого узора быть не может. Ведь каждый из них 72 градуса и такого узора быть не может. Тем не менее я держал в руках лист с таким узором.
"Это ещё что!" в жуткой тишине повторил Математик "А что ты скажешь на это?" И с любезной улыбкой протянул мне многогранник, склеенный из простой бумаги. Не смотря на безобидность материала, из которого он был сделан, сила его превосходила силу гранатного взрыва. Все его грани были правильными шестиугольниками. "Я назвал его "гексаиксоидом" - усмехнулся автор безумства. Безнадёжно вздохнув, я попытался померить углы. Многогранник был правильным в полном смысле этого слова и в каждой его вершине, как и у додекаэдра по три правильные шестиугольные грани. Но когда Математик вынул ещё один многогранник, составленный из правильных восьмиугольников, я понял что дело плохо. "Несомненно я сошёл с ума" - обречённо подумал я.

Сон второй
"Слышал ли ты о трисекции угла?" - спросил Математик.
"Слышал" - ответил я устало. "Это деление угла на три равных части. Его нельзя выполнить при помощи циркуля и линейки"
"Кто сказал тебе подобную глупость" - возмутился он.
"Я когда-то читал об этом"
"О, Боже, о какой только ерунде не пишут!!! Я покажу тебе изящное решение этой задачи, сделанное мной лично!" Он достал чистый лист бумаги, линейку и циркуль. "Смотри внимательно!" и начал выполнять чертёж. Пока он чертил угол, я довольно спокойно смотрел на него. Но когда он перешёл к делению угла , мне пришлось предельно напрячь внимание, чтобы не упустить подробности. Я хорошо знаю геометрию! По крайней мере ещё недавно я был в этом уверен. Но несмотря ни на что я не смог заметить ошибки в его доказательстве. "Действительно изящно" - мысленно усмехнулся я. И я выхватил у него из рук лист ещё раз проверил чертёж." Да он просто маг и волшебник" - подумал я.
Маг и волшебник удовлетворённо усмехнулся, и взяв у меня из рук чертёж сказал: "Это все, конечно, хорошо, но не идет ни в какое сравнение со следующим моим открытием. Я мысленно застонал. И какой чёрт дёрнул меня придти к нему? Сидел бы сейчас дома и не подвергался этим нечеловеческим пыткам.
"Помнишь ли ты о том, что древние пытались построить квадратуру круга? То есть квадрат равный по площади данному кругу?"
"Помню" - покорно сказал я.
"Но я уверен, что ты думаешь что это невозможно!"
"Да" - согласился я, решив ничему не возражать.
"Я привык к людской глупости, но я тебе покажу!!!" Он вынул очередную пачку листов. "Смотри!" - воскликнул он швыряя её мне. Листы разлетелись в разные стороны и мне удалось поймать несколько. Кто бы сомневался! На них было это самое доказательство.
Какая досада! Видимо не только я но и Мир сошёл сума.

Сон третий
"Всё это расчудесно!" - сказал Математик. "Но всё это и в подмётки не годиться тому, что открылось мне теперь! Параллельные линии Существуют!!!"
Он выразительно поднял вверх указательный палец и потряс им. И хоть я давно сошёл с ума, ему удалось меня удивить.
"Как существуют? Это же невозможно!"
" Для меня нет ничего невозможного!!!" Маг и волшебник встал в позу и перед ним появились две тонкие прямые линии.
"Смотри внимательно!". Я взглянул. Насколько достигал мой взгляд линии шли на равном расстоянии друг от друга и не сходились даже по законам перспективы. Но я устал удивляться. "Это невозможно" - повторился я.
"О! Честь открытия принадлежит не только мне."
"Неужели они и вправду не пересекуться?" Я смутно вспоминал что в детстве читал про что-то подобное. Вроде бы это была книжка математических курьезов. Был в древности какой-то чудак, кажеться его звали Евклидом, который считал это за аксиому.
"Только изощрённый ум мог вообразить себе такое" - воскликнул я.
"Ну зачем ты так?" - возразил Математик. "Разве ты не видишь, что Евклид прав!"
"Вижу. Но кто поручиться что дальше, куда не достаёт мой взгляд, всё остаётся по прежнему.
"Ах вот как?!" - возмутился он. "То, что ты сомневаешься во мне или Евклиде еще ладно! Но ты же видишь это!" И он ткнул пальцем а линии.
"И что?" - возмутился я. "Главное, на что покушается твоё с Евклидом открытие - это бесконечность!Ты представляешь что станет с пространством, если твои линии и впрямь бесконечны?"
"Ладно!" - сказал Математик. "Сомнения надо искоренять. Мы с тобой лично проверим правильность этого гениального открытия!"
"Гениального?" - с сарказмом спросил я.
"ДА! ДА! И мы будем проверять это сами".
"Но как? Разве такие вещи поддаются практической проверке?
"Ещё как поддаются! Мы с тобой будем двигаться вдоль этих линий пока не увидим их пересечение или не заметим их расхождение. И мы с тобой пойдём в разные стороны. Надеюсь, хе, хе мы не встретимся!"
"Как в разные? - испугался я.
"Только в разные! Ты в одну, я в другую. Надеюсь, когда мы расстанемся навсегда и удалимся в разные стороны пространства, ты поймёшь - что я и Евклид были правы!" Конечно" - добавил он после некоторого раздумья - "Можно бы проверить это и другим способом. Но только этот прямой и непосредственный."
И мы стали проверять. С тех пор я лечу вдоль этих линий, лечу всё дальше и дальше, а они продолжают оставаться параллельными! Прошли уже три миллиона, восемь тысяч, сто пятьдесят лет и десять месяцев, а я продолжаю проверку. Вы спросите Как я засекаю время? А не знаю! Чувствую и всё. Математик тоже скользит вдоь линий в другую сторону. Часто я проклинаю себя - и зачем я ввязался в эту авантюру? Мне иногда просто невмоготу видеть эти линии идущие на одном расстоянии друг от друга, строго на одном! Но одна мысль всё чаще посещает меня - "Бесконечность впереди - это жутко!" Но самая жуткая из мыслей посещающих меня, от которой я почти теряю сознание - "Неужели они никогда не пересекутся?!

Серия сообщений "Анекдоты, юмор, смешные истории ":
Часть 1 - Анекдоты о блондинках
Часть 2 - Анекдоты про инопланетян
...
Часть 23 - Котоматрицы
Часть 24 - Звериный позитив
Часть 25 - Кошмар математика в трёх снах (Шутка)

Серия сообщений "Стихи":
Часть 1 - Волшебник граффити
Часть 2 - Зимний пейзаж
...
Часть 14 - Танец красок
Часть 15 - Тигр. Стихи Уильяма Блейка
Часть 16 - Песня художника
Часть 17 - Мои стихи на Самиздате

http://lenta.ru/articles/2012/07/31/fractal/ 

Архаичная геометрия природы

Фрактальный анализ помог обнаружить следы строительства древних пирамид

 

Немецкие геологи помогли археологам - используя фрактальный анализ, они смогли доказать, что в окрестностях Дахшура - некрополя фараонов Древнего и Среднего царств в Египте - люди в далеком прошлом вели активное строительство. Видимых глазу следов строений не осталось, но оказалось, что вмешательство человека в естественные процессы эрозии отпечаталось в самой структуре каналов. На первый взгляд это открытие может показаться экзотичным, но геометрические методы в геологии, даже такие, как фрактальный анализ, давно стали обычным делом.

 

Предки современных фракталов

 

В конце XIX века математики были озабочены вопросами, которые позже привели к возникновению топологии, законченной теории интегрирования и многим другим фундаментальным результатам. Тогда же зародились и первые предки фракталов, простейшим представителем которых можно считать канторово множество. Как это часто бывает, впервые этот объект появился в работе вовсе не Георга Кантора, а математика из Оксфорда Генри Смита в 1875 году. Вот как он сам описывал построение тогда еще безымянного объекта (pdf):

"Пусть дано некоторое целое число m. Разобьем отрезок от 0 до 1 на m равных частей и выкинем последний кусок (предлагается выкидывать интервал - то есть отрезок без граничных точек - прим. "Ленты.ру"). Затем оставшиеся m - 1 куска разобьем на m равных частей и из каждого снова выкинем по последнему. Продолжая так ad infinitum (то есть до бесконечности - прим. "Ленты.ру"), получим бесконечное число точек на отрезке."

 

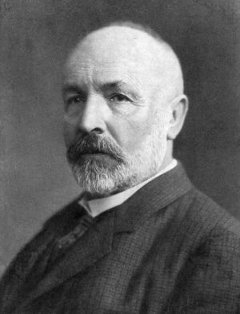Георг Кантор

 

Работа Смита прошла почти незамеченной специалистами и множество было переоткрыто уже немецким математиком Георгом Кантором в 1883 году. На самом деле само множество Кантор не строил, он строил функцию, которая позже получила название канторовой лестницы - важный пример в теории интегрирования (в определение которой вдаваться не будем). Более того, никакие отрезки Кантор не рассматривал - его подход был чисто арифметическим.

Он рассуждал следующим образом. Рассмотрим точки на отрезке от 0 до 1 в троичной системе счисления. Все числа в этой системе записываются "десятичной" дробью, в записи которой присутствуют только 0,1 и 2. Например, 0,1₃ равно 1/3 в десятичной и так далее. Канторовым множеством называется множество чисел, в записи которых фигурируют только 0 и 2. Оказывается, это почти то же самое, что делал Смит, только в его конструкции m должно быть равно трем и на каждом шаге следует выбрасывать не последний отрезок, а тот, что посередине.

Полученный объект обладает рядом удивительных свойств. Например, на первый взгляд может показаться, что в нем очень мало точек - скорее всего, только граничные точки выкидываемых отрезков. Однако, это не так. Например, точка 1/4 в троичной системе счисления записывается как 0,020202..., поэтому не является граничной, но в канторовом множестве лежит. Более того, самому Кантору удалось доказать, что точек в названном в честь него множестве очень много - столько же, сколько в целом отрезке (математики называют такие бесконечные множества "множествами континуальной мощности"). При этом, к слову, суммарная длина всех выкинутых из отрезка интервалов равна единице, то есть в ходе построения было выкинуто практически все - такие вот математические гримасы бесконечности.

После Кантора и Смита метод построения разных множеств и объектов при помощи бесконечного процесса стал довольно популярен. В 1904 году, например, швед Хегл Кох предложил конструкцию кривой, получившей позже название кривой Коха, или снежинки Коха. Возьмем равносторонний треугольник и разобьем каждую его сторону на три части. Серединные отрезки выкинем, заменив их "рогом", составленным из двух отрезков той же длины, что и выкинутый. Получаем многоугольник с 12-ю сторонами. На каждой из них снова проделаем такую же операцию. Действуя так ad infinitum, получим кривую с двумя замечательными свойствами - ни в какой точке у нее нет касательной, а ее длина равна бесконечности, при том что сама кривая за границы первоначального треугольника не сильно-то и вылезает. Более того, схема построения такова, что любой кусок этой кривой имеет бесконечную длину. Анимацию этого процесса можно посмотреть здесь.

Аналогичным образом строятся и многие другие объекты - например, салфетка Серпинского, кривая Пеано (она же кривая Гильберта) - кривая, которая так хитро изгибается (без самопересечений!), что застилает квадрат; губка Менгера; фрактал Теркотта, используемый при анализе механики разрушения, и многие другие.

 

 

 

Динамические системы и понятие фрактала

 

Перенесемся теперь из конца XIX века в середину XX-го. В это время вовсю идет становление совершенно новой для математики концепции численного эксперимента - благодаря появлению компьютеров самая теоретическая из наук получила в свое распоряжение мощный инструмент для экспериментов. Особенно активно новая концепция применяется в теории динамических систем.

Динамической системой в математике называют некоторое пространство, именуемое фазовым, каждая точка которого характеризует состояние системы. Кроме этого задан закон эволюции - правило, по которому система с течением времени меняет свое состояние. Подобного рода системы применяются, например, при изучении динамики популяций в биологии, генетике, механике, для моделирования работы электронных микросхем и много другого. Находят динамические системы применение и в геологии, например, для моделирования взаимного движения тектонических плит - плиты в этом случае рассматриваются как диски, между которыми есть сухое трение.

 

Множество Мандельброта

 

В конце 50-х годов прошлого века изучением такого рода систем с дискретным временем (то есть в которых переход от состояния к состоянию происходит шагами, а не непрерывно) с помощью численных экспериментов занимался Бенуа Мандельброт. Он рассматривал следующую простую нелинейную систему. В качестве фазового пространства бралась обычная плоскость (то есть состояние системы определялось точкой на плоскости) как множество комплексных чисел. Закон перехода от состояния к состоянию задавался правилом f(z) = z ² + b. То есть, если в n-ый момент времени динамическая система была в состоянии z_n, то в следующий момент она переходила в состояние z_{n + 1} = f (z_n).

Относительно этой системы Мандельброт интересовался вопросом ограниченности траекторий. Под траекторией в данном случае следует понимать последовательность точек z_n, которая, как следует из формул, однозначно определяется своим исходным состоянием z₀. Ограниченность, в свою очередь, означает, что можно выбрать круг достаточно большого радиуса, из которого последовательность z_n не выйдет ни при каком n. Вопрос ограниченности траекторий довольно естественный - в реальных механических системах бесконечный рост фазовых переменных ни к чему хорошему обычно не приводит.

Мандельброт интересовался ограниченностью вполне конкретной траектории, начинающейся в нуле z₀ = 0 в зависимости от параметра b. С помощью компьютера он проводил численный эксперимент, и если за некоторое число шагов точка "убегала" достаточно далеко, то он полагал, что она убегает на бесконечность. В результате ему удалось нарисовать на плоскости множество таких b (пусть и примерно), для которых траектория нуля ограничена.

В 1977 Мандельброт выпустил книгу "Фрактальная геометрия природы", которая состояла преимущественно из таких вот сгенерированных на компьютере картинок для разного рода систем, и некоторого количества не слишком строгих с математической точки зрения рассуждений, призванных обосновать обывателю появление этих самых картинок. Именно в этой книге впервые появился термин фрактал.

Так как книжка носила, в целом, развлекательных характер, то сам термин фрактал не имеет строгого математического определения. Одним из наиболее распространенных вариантов, пусть и немного неформальным, является следующий: фракталом называется геометрическая фигура, имеющая достаточную степень самоподобия. Под самоподобием здесь понимается то, что какие-то составные части фигуры, будучи увеличенными, совпадают с исходным объектом. В каком-то смысле это определение является результатом банальной расшифровки самого названия: fractus по-латински означает дробный, а frangere - ломать.

 

Множество Жюлиа. Строится для той же динамической системы, что и множество Мандельброта по правилу: для фиксированного b отмечаются точки, стартующие из которых траектории ограничены. В данном случае b = -0.70176-0.3842i

 

С точки зрения такого определения канторово множество, о котором речь шла выше, является фракталом - если взять его половину, то есть точки, принадлежащие первому из двух оставшихся на первом шаге отрезков (или, что то же самое, точки в "десятичном" разложении которых первая после запятой цифра - ноль), а потом увеличить это множество в три раза, то получим исходное канторово множество. Этим же свойством обладают куски снежинки Коха, составные части салфетки Серпинского и остальные, упомянутые выше фракталы. Чуть менее очевидно, что этим свойством самоподобия обладает множество Мандельброта - но, как оказалось, так оно и есть.

 

Размерность и геология

 

Множество Мандельброта показывает, что фракталы естественным образом возникают в динамических системах. Именно через этот раздел математики и физики они попали в геологию. Однако прежде чем перейти к приложениям, нам потребуется один из основных инструментов фрактального анализа - размерность.

Размерность в топологии бывает самая разная. Простейшая - это так называемая топологическая размерность. Не вдаваясь в подробности, можно сказать, что топологическая размерность точки равна нулю, прямой (отрезка) - единице, плоскости (плоской фигуры, например, круга) - двум, пространства - трем. Интуитивно понятно, что размерность, например, канторова множества равна нулю (не зря его еще называют канторовой пылью), кривых Коха и Пеано - единице и так далее.

 

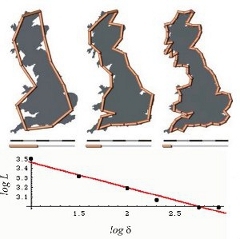Метод Ричардсона вычисления размерности береговой линии британских островов. Иллюстрация В.Захаров/Динамические системы и фракталы в геологии

 

Помимо топологической размерности, для фракталов определена так называемая фрактальная размерность. Представим, что у нас есть береговая линия, например, Великобритании, и мы хотим измерить ее протяженность. Логично для этого использовать линейку - то есть мы будем приближать сложную форму береговой линии к ломаной с одинаковыми звеньями. При попытке реальных измерений выяснится, что с уменьшением линейки длина береговой линии растет, причем растет экспоненциально (правда, до определенного момента)!

Это, конечно, удивительно, но с таким эффектом мы уже встречались - ломаные, которые мы строили для получения кривой Коха, можно считать приближениями конечного фрактала. Каждая ломаная имеет конечную длину, но можно показать, что с каждым шагом эта длина растет экспоненциально и неограниченно.

Теперь представим, что фрактал уменьшили в r раз. Сколько копий N уменьшенного фрактала потребуется, чтобы накрыть первоначальный объект? Оказывается, ответ на этот вопрос такой же, как и в случае с береговой линией, то есть связан с некоторой экспонентой: N примерно равно r^D. Оказывается показатель D определяется однозначно и именно его называют фрактальной размерностью объекта. Соответственно более строгое определение фрактала звучит так: фрактал - это объект, топологическая размерность которого меньше фрактальной (это условие носит название неравенства Мандельброта). Для всех рассмотренных нами фракталов это условие выполнено. Например, фрактальная размерность канторова множества чуть больше 0,63, кривой Коха - больше 1,26, кривой Пеано - в точности 2 (из этого, кстати, следует, что довольно популярное определение фрактала как объекта дробной размерности не слишком удобно).

Однако, фрактальная размерность - это математическая абстракция, поэтому возникает вопрос, как ее вычислять на практике, для реальных объектов? Один метод (которым и ограничимся), оказывается, уже сформулирован - это метод Ричардсона, используемый для подсчета размерностей кривых, в том числе и береговых линий. Для того чтобы оценить размерность объекта, достаточно построить график зависимости логарифма полученной длины кривой от логарифма длины линейки. Например, вычисленная таким образом фрактальная размерность земных континентов и крупных островов составляет примерно 1,22.

Для чего нужна фрактальная размерность? Оказывается, она позволяет обнаружить совершенно неожиданные соотношения в природе. Например, площадь континента или крупного острова S соотносится с его периметром по формуле S примерно равно P^2/D, где D - фрактальная размерность. Аналогичные соотношения существуют на массу и периметр, массу и диаметр и многие другие (хоть это и не имеет отношение к обсуждаемой теме, но можно упомянуть, что фрактальная размерность натурального пуха равна 1,6).

 

Некрополь и черновые пирамиды

Некоторое время назад в Quaternary International появилась статья немецких геологов. В этой работе они применили упомянутый выше фрактальный анализ в помощь археологам. Однако, обо всем поподробнее.

Дахшура - известная ныне на весь мир достопримечательность Египта к югу от Каира. В далеком прошлом это было священное место, некрополь - здесь хоронили правителей Древнего и Среднего царств примерно 4,5 тысячи лет назад. Согласно современным представлениям, именно здесь египтяне оттачивали навыки строительства пирамид - в Дахшуре сохранились пирамиды странных форм. Например, Ломаная пирамида Снофру - это пирамида, наклон сторон которой резко меняется на полпути к вершине.

 

Ломаная пирамида. Фото Néfermaât/Wikicommons

 

Сам некрополь относительно небольшой - площадью 1,3 на 5 километров. За 4,5 тысячи лет следы людского вмешательства на этой территории почти полностью стерлись. Однако геологи предположили, что даже если видимых следов вмешательства не осталось, следы строительства, которое велось на территории некрополя, можно обнаружить в структуре рельефа и естественных водных каналов в регионе.

Для региона ученые вычисляли два параметра. Первый - это фрактальная размерность сети каналов. Известно, что такого рода сети (как и русла рек) являются в некотором смысле самоподобными деревьями, для которых фрактальная размерность больше топологической, которая в данном случае равна единице. Второй параметр был несколько хитрее - ученые брали компьютерную модель рельефа и считали ее фрактальную размерность. Они предположили, что, так как рельеф в этой местности формируется преимущественно под воздействием потоков воды, эти два параметра должны быть связаны, то есть коррелировать.

В результате ученым удалось обнаружить, что корреляция тем меньше, чем ближе к пирамидам. Из этого они заключили, что слабая взаимосвязь между этими двумя размерностями и есть показатель вмешательства в процесс человека, его след. Исследователям удалось даже оценить примерную площадь вмешательства - около 6 квадратных километров вокруг Дахшура. Скорее всего, пробное строительство велось во времена Сниферу - первого фараона IV династии и отца

 Хуфу (известного также как Хеопс), фараона, построившего самую известную из великих пирамид.

Сами исследователи пока аккуратно говорят о своем открытии - для того, чтобы убедиться, что человеческое вмешательство связано с корреляцией двух фрактальных размерностей, потребуется время. Однако если их результаты подтвердятся, археологи приобретут замечательный и совершенно неожиданный инструмент для поиска мест для будущих раскопок. И это будет здорово. 

http://ushilapyhvost.ru/blog/43173792992/Malenkaya...173792992&bpid=43173792992 

Маленькая собачка нашла и усыновила брошенного котенка

развернуть

Это трогательная история о маленькой собачке, которую спасли  вместе с усыновленным ею котенком. 

В городе Андерсон, Южная Каролина, инспектор по бродячим животным офицер Мишель Смит обнаружила у насыпи за ручьем необычную парочку. Маленькую собачку, которая вылизывала крошечного котенка и кормила его своим молоком.
 

Инспектор прибыла по заявке местного жителя, который два дня подряд слышал в этом месте собачий лай. Собаку вместе с котенком доставили в приют для животных и посадили в одну клетку, так как разлучать их всем показалось бесчеловечным. Собака  заботилась о малыше как о родном щенке.
 

Мишель Смит считает, что собака нашла этого котенка у ручья, что она специально спустилась за ним вниз с насыпи, возможно услышав как он мяукает, а выбираться с ним наверх не стала или не смогла. Это объясняет, почему они находились в таком неудобном месте. Котенка же вероятно кто-то просто выкинул или хотел утопить. И может быть собака лаяла как раз для того, чтоб привлечь внимание людей.
 

Еще по теме

13:38 Алиса и Маркиз +5 4

09:56 Красных волчат чудом спасли от смертельного вируса +7

09:54 Хохлатый дикобраз из Швейцарии +4 1

все темы →

Собака не выглядела бродячей, она была упитанной и ухоженной, модно стриженной. Возможно, что она убежала из дома. Сейчас собака в приюте ждет, когда истечет 14-дневный срок, в который должен объявится ее хозяин. Если же никто не придет, собаку и котенка выставят на усыновление в новые семьи.

Источник 

Интересный материал с сайта: http://ushilapyhvost.ru/blog/43016365190/Ulyibayus...het-stat-novyim-internet-hitom 

Улыбающийся кот может стать новым интернет-хитом

развернуть

Вам надоел вечно сердитый Grumpy Cat? Тогда у нас для вас хорошие новости. В интернете появилась полная его противоположность, Счастливый кот (Happy Cat).

Три фотографии своего кота, который словно все время улыбается, выложил в блоги reddit пользователь под ником sketchampm. Он написал, что несколько месяцев назад просто случайно обнаружил этого кота на своем крыльце.

Бродяга отчаянно мяукал, у блоггера сжалилось сердце и он оставил животину у себя. Может поэтому у кота такой довольный вид?

Еще по теме

11:15 На службе в полиции "работает" необычный сотрудник - обезьянка +4 1

10:03 Животные и их детёныши +6 4

09:53 Китайцы заводят собак, чтоб защищаться от землетрясений +11

все темы →

 

Источник 

Серия сообщений "Анекдоты, юмор, смешные истории ":
Часть 1 - Анекдоты о блондинках
Часть 2 - Анекдоты про инопланетян
...
Часть 18 - Давайте улыбнёмся!!!
Часть 19 - Котоматрица
Часть 20 - Юмор, анекдоты о собаках
Часть 21 - Котоматрица
Часть 22 - Прикольные фотографии котов, сделаные в подходящий момент
Часть 23 - Котоматрицы
Часть 24 - Звериный позитив
Часть 25 - Кошмар математика в трёх снах (Шутка)