Читая книгу посвященную методике преподавания математики (Г.П. Бевз. Методика розв'язування алгебраїчних задач у 6-8 класах) я встретил простую задачу, которая имеет несколько интересных и полезных в методическом отношении (для логического развития учащихся) решений. Вот условие этой задачи в моем вольном переводе с украинского языка.

Сумма цифр двузначного числа рана 15. Если это число умножить на 7 и от произведения отнять двузначное число, записанное теми же цифрами что и данное, но в обратном порядке, то получим 387. Найти двузначное число.

Первое, что я сделал - нашел свое, как мне кажется, самое простое решений этой задачи, доступное даже учащимся младших классов. Вот эта задача и ее несколько решений.

Решение 1.

Так как сумма цифр двузначного числа рана 15, то возможно это число 69, 78, 87 и 96. Не так уж много кандидатов на правильный ответ. Теперь проверим каждое из этих число на выполнение условия "Если это число умножить на 7 и от произведения отнять двузначное число, записанное теми же цифрами что и данное, но в обратном порядке, то получим 387".

69 ⋅ 7 - 96 = 387. Значит, 69 - искомое число.

Однако задача может иметь и другие решения. Поэтому проверим оставшиеся числа (78, 87 и 96) на выполнение этого условия.

78 ⋅ 7 - 87 (оканчивается на 9) ≠ 387.

87 ⋅ 7 - 78 (оканчивается на 1) ≠ 387.

96 ⋅ 7 - 69 (оканчивается на 3) ≠ 387.

Значит, 69 - единственное искомое число.

Ответ: 69.

Рассмотренный мною метод решения этой задачи называется методом перебора. Он эффективен тогда, когда кандидатов для выбора среди них не так много.

Автор, указанной выше книги решает эту задачу следующими двумя способами.

Решение 2.

Обозначим цифру десятков искомого двузначного числа через х. Тогда цифра его единиц будет 15 - х, поэтому искомое число равняется 10х + 15 - х; 10(15 - х) + х - число, записанное теми же цифрами, но в обратном порядке. Получаем уравнение

(10х + 15 - х) ⋅ 7 - (10(15 - х) + х) = 387.

Решив это уравнение получим х = 6 (цифра десятков). Цифра единиц: 15 - х = 9.

Ответ: 69.

Решение 3.

Обозначим цифру десятков искомого двузначного числа через х, а цифру единиц - через у. Так как сумма цифр равна 15, то получаем уравнение х + у = 15. Кроме этого из условия задачи следует еще одно уравнение: (10х + у) ⋅ 7 - (10у + х) = 387, 69х - 3у = 387, 23х - у = 129.

Получаем систему уравнений

которая имеет единственное решение х = 6, у = 9.

Ответ: 69.

Вот такие решения предлагает нам автор пособия по методике преподавания алгебры. Не знаю почему, но Г.П. Бевз не указа еще одного решение рассматриваемой задачи.

Решение 4.

Обозначим цифру десятков искомого двузначного числа через х, а цифру единиц - через у. Из условия задачи следует уравнение: (10х + у) ⋅ 7 - (10у + х) = 387, 69х - 3у = 387, 23х - у = 129, 23х = 129 + у.

Так как у ≥ 1 (у - первая цифра двузначного числа, поэтому у ≠ 0) и у ≤ 9, то 130 = 129 + 1 ≤ 129 + у ≤ 129 + 9 = 138.

Поэтому 130 ≤ 23х ≤ 138, 5, 652... ≤ 23х ≤ 6. Значит, х = 6.

23 ⋅ 6 = 129 + у, у = 138 - 129, у = 9.

Ответ: 69.

Среди многочисленных школьных математических задач особо выделяются сюжетные задачи. Их также называют текстовыми.

Выделяют два основных метода решения сюжетных задач - арифметический и алгебраический.

До 70-х годов прошлого столетия основным методом решения задач в курсе математики был арифметический метод. Однако позднее за счет алгебраизации курса математики начальной и неполной средней школы из программы было практически вытеснено изучение разнообразных арифметических приемов решения текстовых задач. Самым распространенным методом решения задач стал алгебраический.

Но еще тогда А.Н. Колмогоров предостерегал от чрезмерного увлечения алгебраическим методом.

Практика показала справедливость его предупреждения.В настоящее время еще раз возникла необходимость пересмотра содержания обучения математике (в частности, арифметике). В последние годы появилась методическая литература, в которой наметилась тенденция возвращения к арифметическим способам решения задач.

Мне не хотелось бы, что все пошло по замкнутому кругу. Каждый из методов решения текстовых задач имеет свои преимущества и свои недостатки. Поэтому в школьном курсе математики следует изучать оба метода.

Пример. Сумма двух чисел равна 38. Найти эти числа, если 2/3 первого числа равны 3/5 второго.

Решение 1.

Пусть первое число составляет 90 (90 делится на 2, на 3 дважды и на 5) частей. Тогда его 2/3 будут равны 60 частям. 60 : 3/5 = 100 - столько частей составляет второе число.

Сумма двух чисел равна 90 + 100 = 190 частей. Тогда первое число равно 38 : 190 * 90 = 18, а второе - 38 - 18 = 20.

Проверка. 2/3 от числа 18 равно 12, а 3/5 от числа 20 составляют тоже 12. Значит задача решена верно.

Решение 2.

Пусть первое число равно х, а второе - у. Тогда

Решив эту систему мы получим х = 18, а у = 20.

Конечно, эту задачу можно было бы решить при помощи только одного уравнения.

Однако мне не нравится, что в в приведенных выше решениях арифметический и алгебраический методы "разобщены".

Рассмотрим еще одно решение, в котором оба метода мирно сотрудничают (в отличии от их сторонников и противников).

Решение 3.

Пусть первое число равно х, а второе - у. Тогда , .

Значит, первое число составляет 9 частей, а второе - 10. Тогда на все число будет приходиться 9 + 10 = 18 частей. Поэтому первое число равно 38 : 19 * 9 = 18, а второе - 38 : 19 * 10 = 20.

Проверку я пропускаю, но она обязательный элемент решения.

Последнее решение мне нравится больше всех, так как здесь реализованы все методические преимущества обоих методов.

В поисках интересных задач я нашел еще одну задачу, которую принято относить в виду задач "на клетчатой бумаге". Думаю, что их методическая ценность до сих пор занижена. Эти задачи позволяют хорошо усваивать материалы для запоминания, развивают не только моторику (что уже поздно для учащихся старших классов), но конструктивизм в поисках решений новых задач.

Вот эта задача.


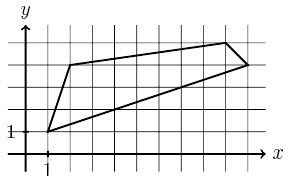
Задача. Найдите центр окружности, описанной около четырехугольника на рисунке.

Решение. Эту задачу я решал так называемым "методом проб и ошибок". Просто прикинул на глаз, где может быть центр искомой окружности и определил координаты этой точки.

Конечно первая попытка привела меня к неудаче. Простейшие вычисления на применение теоремы Пифагора показали, что я ошибся. Но ничего страшного, пришлось немного поправить мою гипотезу и, искомая точка была быстро найдена: (6; 1).

Повторное применение теоремы Пифагора показали, что точка (6; 1) действительно является центром данного четырехугольника. При этом появился повод для рассказа о том, что прямоугольный треугольник со сторонами 3, 4 и 5 называется Египетским.

Эта задача хороша для закрепления темы: "Вписанные и описанные окружности". Ее, на мой взгляд, следует отнести к так намазываемым дидактическим задачам.

Вот еще несколько задач из болгарских источников

Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 10 - ДЕФОРМИРОВАННЫЕ УПРАЖНЕНИЯ - СРЕДСТВО ФОРМИРОВАНИЯ ГЛУБОКИХ И ПРОЧНЫХ ЗНАНИЙ
Часть 11 - Окружность описанная около трапеции
Часть 12 - Центр окружности, описанной около четырехугольника
Часть 13 - Wolfram Alpha для браузера
Часть 14 - Задача из рассказа «Репетитор» Антона Павловича Чехова
...
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения

Бродя по просторам Интернета на одном из болгарских форумов (форум сайта http://estoyanov.net/,) я наткнулся на очень интересную задачу. Вот ее текст на болгарском языке.

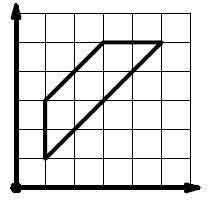Задача 1. Намерете координатите на центъра и дължината на радиуса на окръжността, описана около четириъгълника на рисунката, ако страната на квадратчетата е 1.

Нетрудно понять ее условие. Однако для тех, кто "в танке" вот ее перевод на русский язык.

Задача 1. Вычислите координаты центра и длину радиуса окружности, описанной около четырехугольника, если сторона клетки на рисунке равна 1.

На мой взгляд, это задача очень красивая. Ее легко решить почти устно. Вот мои ответы: (4; 2), √10.

Думаю, что такие задачи необходимо использовать на уроке после изучения темы "Описанная окружность". К сожалению, в русскоязычной литературе таких задач практических нет. А жаль!

Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 9 - А МОЖНО МЕТОДОМ ПЕРЕБОРА?
Часть 10 - ДЕФОРМИРОВАННЫЕ УПРАЖНЕНИЯ - СРЕДСТВО ФОРМИРОВАНИЯ ГЛУБОКИХ И ПРОЧНЫХ ЗНАНИЙ
Часть 11 - Окружность описанная около трапеции
Часть 12 - Центр окружности, описанной около четырехугольника
Часть 13 - Wolfram Alpha для браузера
...
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения