-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Задание 1 профильного ЕГЭ 2015 года |
Вот эта супер-мупер задача.
1. В доме, в котором живет Игорь, один подъезд. На каждом этаже по шесть квартир. Игорь живет в квартире 47.
На каком этаже живет Игорь?
Обязательно предложу эту задачу ученику начальной школы, например, первого или второго класса. Для ученика третьего класса эта решение этой задачи ничего полезного не принесет, а будет, как говорят сторонники теории развивающего обучения, топтанием в зоне актуального развития.
От учеников первого или второго классов жду таких решений.
Решение I.
1 этаж - квартиры 1 - 6, 2 этаж - квартиры 7 - 12, 3 этаж - квартиры 13 - 18, 4 этаж - квартиры 19 - 24, 5 этаж - квартиры 25 - 30, 6 этаж - квартиры 31 - 36, 7 этаж - квартиры 37 - 42, 8 этаж - квартиры 43 - 48. Значит, Игорь живет на восьмом этаже.
Вот такое простое решение, минимум математики (на уровне первого класса) и куча рассуждений на уровне дебила-выпускника средней школы.
Решение II.
Седьмой этаж завершится квартирой 42, а восьмой - 48. Значит, квартира 47 находится на восьмом этаже.
Здесь хоть есть мышление на уровне среднего ученика третьего класса.
Так и хочется написать, что эту задачу я даже не стану предлагать учащимся среднего, а тем более старшего звена. Но это будет неправдой. Обязательно предложу, но в другой формулировке.
В доме, в котором живет Игорь, один подъезд. На каждом этаже по n квартир. Игорь живет в квартире N.
На каком этаже живет Игорь?
При этом буду ждать несколько решений, среди которых следующее.
Решение III.
Пусть Игорь живет на этаже с номером х, тогда

Значит,
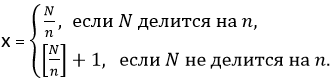
Решение этой задачи в такой формулировке, конечно, будет намного полезнее, чем в формулировке ее авторов.
1. В доме, в котором живет Игорь, один подъезд. На каждом этаже по шесть квартир. Игорь живет в квартире 47.
На каком этаже живет Игорь?
Обязательно предложу эту задачу ученику начальной школы, например, первого или второго класса. Для ученика третьего класса эта решение этой задачи ничего полезного не принесет, а будет, как говорят сторонники теории развивающего обучения, топтанием в зоне актуального развития.
От учеников первого или второго классов жду таких решений.
Решение I.
1 этаж - квартиры 1 - 6, 2 этаж - квартиры 7 - 12, 3 этаж - квартиры 13 - 18, 4 этаж - квартиры 19 - 24, 5 этаж - квартиры 25 - 30, 6 этаж - квартиры 31 - 36, 7 этаж - квартиры 37 - 42, 8 этаж - квартиры 43 - 48. Значит, Игорь живет на восьмом этаже.
Вот такое простое решение, минимум математики (на уровне первого класса) и куча рассуждений на уровне дебила-выпускника средней школы.
Решение II.
Седьмой этаж завершится квартирой 42, а восьмой - 48. Значит, квартира 47 находится на восьмом этаже.
Здесь хоть есть мышление на уровне среднего ученика третьего класса.
Так и хочется написать, что эту задачу я даже не стану предлагать учащимся среднего, а тем более старшего звена. Но это будет неправдой. Обязательно предложу, но в другой формулировке.
В доме, в котором живет Игорь, один подъезд. На каждом этаже по n квартир. Игорь живет в квартире N.
На каком этаже живет Игорь?
При этом буду ждать несколько решений, среди которых следующее.
Решение III.
Пусть Игорь живет на этаже с номером х, тогда
Значит,
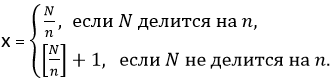
Решение этой задачи в такой формулировке, конечно, будет намного полезнее, чем в формулировке ее авторов.
|
ВЛАДЕЛЬЦЫ ДВУХ ЗАВОДОВ |
Так называется задача 19 на досрочном экзамене ЕГЭ по математике в 2015 году. Эта задача теперь решается принципиально иначе, чем в тексте демоварианта.
Предлагаю Вашему вниманию видеоролик посвященный решению этой задачи и еще три тестовых задания на эту же тему.
А вот еще один видеоролик по решению этой же задачи.
Вот такие некрасивые решения этой задачи. После такого моего заявления некоторые сочтут это задание не достойным их внимания. У нас всегда так, если мы не можем найти красивое решение какой-либо задачи, то в этом виновата, конечно, задача, но не мы сами.
Такая же ситуация и здесь. Нашли Интернете одно решение и не пытаемся искать другие. А зря. Эта задача имеет еще несколько решений.
Пусть первый завод работал х часов, а второй - у часов. Тогда 2х + 5у = 580. При этом выплаченная сумма будет равна 500(х2 + у2).
Нам нужно найти минимум функции 500(х2 + у2) при условии 2х + 5у = 580. Мы пришли к известной математической задаче о вычислении экстремума функции при заданном ограничении на перемененные, т. е. к так называемой задаче на условные экстремумы.
В курсе высшей математики разработаны специальные методы решения этой задачи. нам же придется ограничиться знаниями элементарной (школьной) математики. при этом предлагаем несколько решений этой задачи с опорой на различные наборы знаний.
Решение II (геометрическое).
Решение III (формулы приведения).

При этом равенство имеет место тогда и только тогда, когда выполняется система уравнений
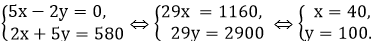
Значит, 5 800 000 - ответ нашей задачи.
Ответ: 5 800 000.
Согласитесь, красивое и простое решение этой задачи. Однако я здесь использовал одну элементарную формулу
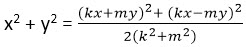
Задачи для самостоятельного решения
1. Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся t2 часов в неделю, то выпускают t единиц продукции. А если рабочие второго завода суммарно трудятся t2 часов в неделю, то выпускают 2t единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час. Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?
2. Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, - 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Предлагаю Вашему вниманию видеоролик посвященный решению этой задачи и еще три тестовых задания на эту же тему.
А вот еще один видеоролик по решению этой же задачи.
Вот такие некрасивые решения этой задачи. После такого моего заявления некоторые сочтут это задание не достойным их внимания. У нас всегда так, если мы не можем найти красивое решение какой-либо задачи, то в этом виновата, конечно, задача, но не мы сами.
Такая же ситуация и здесь. Нашли Интернете одно решение и не пытаемся искать другие. А зря. Эта задача имеет еще несколько решений.
Пусть первый завод работал х часов, а второй - у часов. Тогда 2х + 5у = 580. При этом выплаченная сумма будет равна 500(х2 + у2).
Нам нужно найти минимум функции 500(х2 + у2) при условии 2х + 5у = 580. Мы пришли к известной математической задаче о вычислении экстремума функции при заданном ограничении на перемененные, т. е. к так называемой задаче на условные экстремумы.
В курсе высшей математики разработаны специальные методы решения этой задачи. нам же придется ограничиться знаниями элементарной (школьной) математики. при этом предлагаем несколько решений этой задачи с опорой на различные наборы знаний.
Решение II (геометрическое).
Решение III (формулы приведения).
При этом равенство имеет место тогда и только тогда, когда выполняется система уравнений
Значит, 5 800 000 - ответ нашей задачи.
Ответ: 5 800 000.
Согласитесь, красивое и простое решение этой задачи. Однако я здесь использовал одну элементарную формулу
1. Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся t2 часов в неделю, то выпускают t единиц продукции. А если рабочие второго завода суммарно трудятся t2 часов в неделю, то выпускают 2t единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час. Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?
2. Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, - 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
|
Процитировано 3 раз
Прием решения уравнения в целых числах |
 Решите в натуральных числах уравнение 3⋅2х = у2 - 1.
Решите в натуральных числах уравнение 3⋅2х = у2 - 1.Такое уравнение я решал во время занятия с одной десятиклассницей, желающей получить хорошее математическое образование.
Известно, что тема диафантовы уравнения изучаются в средней общеобразовательной школе факультативно, но включены во многие олимпиады различного уровня для школьников. Данное уравнение, как и многие другие диафантовы уравнения, не имеет общего алгоритма решения, а есть только некоторые приемы его решения, которые можно применить к данному уравнению и, как было сказано, к не большому классу аналогичных задач.
Наше уравнение можно переписать так: 3⋅2х = (у - 1)(y + 1).
Если бы не было множителя 3 в левой части уравнения, то можно было бы применить известный мне прием, суть которого состоит в том, что у - 1 и y + 1 стали бы делителями 2х и, значит также имели бы вид 2t. А дальше дело техники.
Поэтому мне надо как то избавиться от множителя 3. Это я и постараюсь сделать.
Левая часть данного уравнения делится на 3 и не делится на другую степень числа 3. Значит только один и только один из множителей у - 1 и y + 1 делится на 3. Поэтому рассмотрим два случая.
I. Пусть у - 1 делится на 3, то есть у - 1 = 3⋅2р, где р - неотрицательное целое число. Тогда у + 1 = 3⋅2х-р.
Здесь следует сделать некоторые пояснения. Так как числа у - 1 и y + 1 отличаются друг от друга на 2, то они оба четные или оба нечетные. Так как левая часть данного уравнения делится на 2, то числа у - 1 и y + 1 оба четные. При этом только одно из них делится 3, значит оно имеет вид 3⋅2р.
Итак мы имеем систему уравнений

Вычитая из второго уравнения первое получим
2х-р - 3⋅2р = 2, 2р(2х-2р - 3) = 2.
Если р = 0, то имеем 1⋅(2х - 3) = 2, 2х = 5 - чего быть не может. Значит, р ≠ 0 и 2р - четное число. Это возможно только при р = 1. Поэтому имеем 2⋅(2х-2 - 3) = 2, 2х-2 - 3 = 1, 2х-2 = 4, х - 2 = 2, х = 4.
Подставив х = 4 исходно е уравнение получим 48 = у2 - 1, у2 = 49 и так y - натуральное число, то y = 7.
Итак, мы получили одно из решений данного уравнения - (4; 7).
II. Пусть у + 1 делится на 3, то есть у + 1 = 3⋅2р, где р - неотрицательное целое число. Тогда у - 1 = 3⋅2х-р.

Как и ранее вычитая из первого уравнения второе получим 2р(3 - 2х-2р) = 2.
Нетрудно доказать, что р ≠ 0. Тогда 2р = 2 и р = 1. В этом случае 3 - 2х-2 = 1, 2х-2 = 2, х - 2 = 1, х = 3.
При х = 3 исходное уравнение примет вид 24 = у2 - 1, у2 = 25, у = 5.
(3; 5) - второе решение данного уравнения.
Ответ: (4; 7), (3; 5).
|
|
Понравилось: 1 пользователю
Технические детали и главная идея |
 В сети Интернет очень много видеокурсов посвященных различным вопросам. Хорошо это или плохо? Думаю, что хорошо, за исключением одного "НО". Как правило, в этих уроках львиная доля времени уделяется тому, на какую клавишу следует нажать. А это уже очень плохо!
В сети Интернет очень много видеокурсов посвященных различным вопросам. Хорошо это или плохо? Думаю, что хорошо, за исключением одного "НО". Как правило, в этих уроках львиная доля времени уделяется тому, на какую клавишу следует нажать. А это уже очень плохо!Так, например, в видеокурсах, посвященных, например, сервису gmail большое внимание уделяется тому как создать ярлыки для писем. Если бы там рассказывалось о том, что такое ярлыки, как их можно использовать в различных ситуациях я бы ничего против не имел, наоборот приветствовал бы автора курса. Однако многие авторы акцентируют внимание на то на какую кнопку следует нажимать чтобы получить тот или иной ярлык. А вот это уже плохо. Эта чисто техническая информация не достойная запоминанию и тем более записыванию.
В сервисе gmail в правой верхней части окна есть кнопка, на которой изображено колесико - "Настройки". Нажав на это колесико любой может увидеть небольшое меню. В нижней строки этого меню написано "Справка". В поиск по этой справки впишем слово "ярлык" и нам будет выдана информация о том, что такое ярлык и как его создать. Там же, в частности, можно найти информацию о том как создать вложенные ярлыки.
Лучше бы авторы таких видеокурсов по нажиманию на клавиши рассказали о значении тех же ярлыков в информатике, привели больше полезных примеров. А техническую реализацию этих примеров всегда можно организовать при помощи соответствующих справок, help'ов в различных сервисах и программах.
Почему это так важно? Да потому, что сначала нужно знать что мы делаем и лишь только потом как это можно делать при помощи технических справок.
Так я и поступаю на своих занятиях. Сначала рассказал о том что такое ярлык. Показал как у меня организовано хранение информации в программе Evernote и в почте gmail. Затем научил своих учеников пользоваться справкой в почте gmail и дал задание создать папки для хранения писем имеющих соответствующие ярлыки. Среди этих заданий было и задание на создание вложенных папок.
При таком подходе вырастают думающие специалисты, умеющие усваивать идейную информацию и искать техническую реализацию полезных идей.
К сожалению, сегодня выросло поколение специалистов-кнопочников, которые пасуют при любых технических затруднениях, не умеют искать пути выхода из них.
|
|
Структурирование неупорядоченного массива информации при помощи ярлыков |
 Представим себе, что мы набрали большой объем информации, например, статей на различную тематику. Иногда возникает необходимость заново прочитать ту или иную из них. Однако быстро ее найти бывает весьма проблематично, легче найти заново соответствующую страницу в Интернете.
Представим себе, что мы набрали большой объем информации, например, статей на различную тематику. Иногда возникает необходимость заново прочитать ту или иную из них. Однако быстро ее найти бывает весьма проблематично, легче найти заново соответствующую страницу в Интернете.Такая ситуация возникает очень часто. Поэтому весьма актуально не только вовремя скачивать полезную информацию, но правильно организовывать ее их ранение, например, на компьютере.
Мне понравился принцип организации хранения информации (файлов) при помощи ярлыков.
Что же такое ярлык, для чего нужны они нужны и как с ними работать в нашей ситуации - вот об этом мы поговорим в этой заметке. Не будем размазывать кашу по тарелке, а сразу же обратимся к серьезному источнику знаний - Википедии.
Согласно определению Википедии
Ярлык (англ. shortcut) — файл, служащий указателем на объект (например, файл, который требуется определённым образом обработать), программу или команду и содержащий дополнительную информацию.
Как на практике организуется хранение информации при помощи ярлыков? Сначала всем объектам (единицам полезной информации) присваиваются ярлыки. При этом одному и тому же объекту (файлу) можно присваивать несколько различных ярлыков, характеризующих этот объект с различных точек зрения.
При этом сами объекты хранятся в базе данных без всякой организации, структуры, классификации, как говорится навалом, не систематизированной кучей.
Удаление того или иного ярлыка никак не приводит к автоматическому удалению самого объекта (файла) из базы данных.
Здесь я описал только сам принцип организации хранения, а если быть точнее структурирования большого массива данных, информации при помощи ярлыков. Техническая реализация этой продуктивной идеи может быть различной, нам же важен сам принцип применения инструмента ярлыков.
По этому принципу организовано хранение писем в электронной почте gmail. Пользователь почты на этом сервисе может сам создать удобную для него систему хранения полученных и отправленных писем при помощи ярлыков. Например, для меня почта gmail, не только инструмент написания и получения электронных писем, но и то место, где я храню письма-рассылки (полученные мною и мною созданные). При этом быстрый и своевременный поиск нужного мне письма очень важен.
Также можно организовать хранение заметок в программе Evernote. Так я и поступил. Теперь в Evernote я храню всю свою информацию о полезных ссылках на ресурсы Интернета. Их же у меня несколько тысяч. Найти же нужную в данный момент я могу очень быстро.
Там где это технически возможно, хранение информации при помощи ярлыков очень удобно, оно позволяет вам очень быстро найти статью, заметку, ссылку и т. п. в большой куче информации в тот самый, как говорят, пиковый момент, когда она крайне нужна.
|
Неравенства с радикалами |
В этой заметке мы рассмотрим решение одного типа иррациональных неравенств с радикалами. Если быть точнее рассмотрим известные мне решения неравенства типа 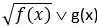 , где f(x) и g(x) - многочлены не выше второй степени.
, где f(x) и g(x) - многочлены не выше второй степени.
В качестве примера рассмотрим неравенство, заимствованное из книги И. И. Мельникова, И. Н. Сергеева "Как решать задачи по математике на вступительных экзаменах" (стр. 89). Скачать эту книгу можно отсюда: https://yadi.sk/d/G1wJWAxFeNqgG.
Решите неравенство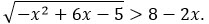
Решение I. Найдем сначала ОДЗ данного неравенства, то есть решим неравенство -х2 + 6х - 5 ≥ 0.
Для этого найдем корни квадратного трехчлена -х2 + 6х - 5. Эти корни мы получим после решения уравнения
-х2 + 6х - 5 = 0,
х2 - 6х + 5 = 0,
D = 36 - 20 = 16 = 42,
x1 = (6 + 4)/2 = 5,
x2 = (6 - 4)/2 = 1,
-(x - 5)(x - 1)≥ 0,
(x - 5)(x - 1)≤ 0.
Решением последнего неравенства будет отрезок [1; 5].
Возводить заданное неравенство в квадрат можно только в случае, когда правая и левая ее части неотрицательны. Поэтому на найденном ОДЗ приходится разбирать два случая.
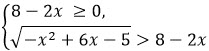 и
и 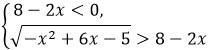
Рассмотрим первый случай, включая туда и ОДЗ.
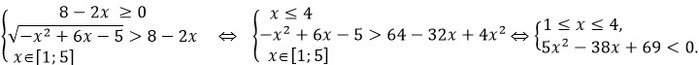
Решим неравенство 5x2 – 38x + 69 < 0.
5x2 – 38x + 69 = 0, D = 1444 – 1380 = 64,
x = (38 ± 8)/10, x1 = 3, x2 = 4,6;
5(x - 3)(x – 4,6) < 0,
Так как х ≤ 4, то x – 4,6 < 0 и х – 3 > 0, x > 3. Поэтому х ∈ (3; 4].
теперь второй случай также включая в него ОДЗ.
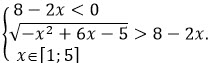
При 8 - 2х < 0 неравенство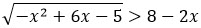 будет выполняться при всех х из ОДЗ. Поэтому будем иметь
будет выполняться при всех х из ОДЗ. Поэтому будем иметь
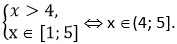
(3; 4] U (4; 5] =(3; 5].
Ответ: (3; 5].
Вот такое решение, конечно по стилю, приводится в указанном выше пособии.
Сейчас я покажу другое решение этого же неравенства.
Решение II.
Не повторяясь отмечу, что ОДЗ данного неравенства - отрезок [1; 5].
Вместо данного неравенства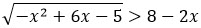 я сначала отмечу, что корнем соответствующего уравнения
я сначала отмечу, что корнем соответствующего уравнения
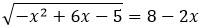
будет единственное число 3 (см. предыдущее решение). Само это число 3, как и число 1, конечно, не является решением данного неравенства. Число же 5, наоборот, является решением данного неравенства.
Число 3 разбивает ОДЗ на два промежутка

На каждом из этих промежутков данное неравенство либо выполняется, либо не выполняется.
Чтобы выяснить это возьмем два числа из этих промежутков: 2 и 4.
При х = 2 данное неравенство не выполняется (проверьте самостоятельно), значит оно не выполняется и на всем промежутке [1; 3].
При х = 4 наше неравенство выполняется, значит оно выполняется и на всем промежутке (3; 5].
Ответ: (3; 5].
Решение II реализовано при помощи так называемого метода интервалов.
Однако ни Решение I, ни Решение II мне не нравятся. Однако это только мое субъективное мнение. И все же мне по душе третье решение данного неравенства.
Решение III.
Это решение - графическое. Для этого надо построить графики двух функций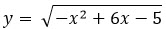 и y = 8 - 2x.
и y = 8 - 2x.
Однако заметим, что
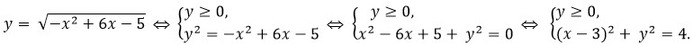
Последняя система задает верхнюю полуокружность с центром в точке (3; 0) и радиусом 2.
После построения в системе координат получим

Не трудно убедиться в том, что точка (3; 2) лежит как на прямой, так и на полуокружности.
Для решения нашей задачи нам нужно найти те значения переменной х, при которых часть полуокружности расположена строго выше части прямой. Это условие выполняется только при х ∈ (3; 5].
Ответ: (3; 5].
Это решение, на мой взгляд, самое лучшее из всех трех решений, которые я привел в этой заметке.
Примечание. Последнее решение не только наглядное, но и позволяет составлять аналогичные задачи учителю и учащимся. Парадокс не задача, не ее текст, а найденное решение реализует технологию развивающего обучения.
В завершение я хотел бы предостеречь моих читателей от типичного заблуждения относительно этих трех решений.
Многие ученики считают, что им нужно освоить, например, только прием из третьего решения, так как оно им нравится. Также есть учителя (и их не мало), которые считают, что им нужно рассказывать своим ученикам только третье решение, так как оно самое изящное, а о двух других решениях не стоит даже вспоминать.
Скажу сразу, что неправы все, как ученики так и учителя. Для того, чтобы стать профессионалом своего дела надо знать все решения данной задачи, даже если некоторые из них не являются рациональными в данном случае. Может случиться так, что прием третьего решение будет трудно реализовать в то время как приемы первого или второго решений останутся единственными из возможных.
В качестве примера рассмотрим неравенство, заимствованное из книги И. И. Мельникова, И. Н. Сергеева "Как решать задачи по математике на вступительных экзаменах" (стр. 89). Скачать эту книгу можно отсюда: https://yadi.sk/d/G1wJWAxFeNqgG.
Решите неравенство
Решение I. Найдем сначала ОДЗ данного неравенства, то есть решим неравенство -х2 + 6х - 5 ≥ 0.
Для этого найдем корни квадратного трехчлена -х2 + 6х - 5. Эти корни мы получим после решения уравнения
-х2 + 6х - 5 = 0,
х2 - 6х + 5 = 0,
D = 36 - 20 = 16 = 42,
x1 = (6 + 4)/2 = 5,
x2 = (6 - 4)/2 = 1,
-(x - 5)(x - 1)≥ 0,
(x - 5)(x - 1)≤ 0.
Решением последнего неравенства будет отрезок [1; 5].
Возводить заданное неравенство в квадрат можно только в случае, когда правая и левая ее части неотрицательны. Поэтому на найденном ОДЗ приходится разбирать два случая.
Рассмотрим первый случай, включая туда и ОДЗ.
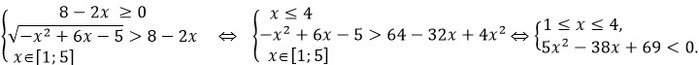
Решим неравенство 5x2 – 38x + 69 < 0.
5x2 – 38x + 69 = 0, D = 1444 – 1380 = 64,
x = (38 ± 8)/10, x1 = 3, x2 = 4,6;
5(x - 3)(x – 4,6) < 0,
Так как х ≤ 4, то x – 4,6 < 0 и х – 3 > 0, x > 3. Поэтому х ∈ (3; 4].
теперь второй случай также включая в него ОДЗ.
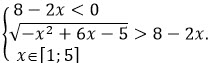
При 8 - 2х < 0 неравенство
(3; 4] U (4; 5] =(3; 5].
Ответ: (3; 5].
Вот такое решение, конечно по стилю, приводится в указанном выше пособии.
Сейчас я покажу другое решение этого же неравенства.
Решение II.
Не повторяясь отмечу, что ОДЗ данного неравенства - отрезок [1; 5].
Вместо данного неравенства
будет единственное число 3 (см. предыдущее решение). Само это число 3, как и число 1, конечно, не является решением данного неравенства. Число же 5, наоборот, является решением данного неравенства.
Число 3 разбивает ОДЗ на два промежутка
На каждом из этих промежутков данное неравенство либо выполняется, либо не выполняется.
Чтобы выяснить это возьмем два числа из этих промежутков: 2 и 4.
При х = 2 данное неравенство не выполняется (проверьте самостоятельно), значит оно не выполняется и на всем промежутке [1; 3].
При х = 4 наше неравенство выполняется, значит оно выполняется и на всем промежутке (3; 5].
Ответ: (3; 5].
Решение II реализовано при помощи так называемого метода интервалов.
Однако ни Решение I, ни Решение II мне не нравятся. Однако это только мое субъективное мнение. И все же мне по душе третье решение данного неравенства.
Решение III.
Это решение - графическое. Для этого надо построить графики двух функций
Однако заметим, что
Последняя система задает верхнюю полуокружность с центром в точке (3; 0) и радиусом 2.
После построения в системе координат получим

Не трудно убедиться в том, что точка (3; 2) лежит как на прямой, так и на полуокружности.
Для решения нашей задачи нам нужно найти те значения переменной х, при которых часть полуокружности расположена строго выше части прямой. Это условие выполняется только при х ∈ (3; 5].
Ответ: (3; 5].
Это решение, на мой взгляд, самое лучшее из всех трех решений, которые я привел в этой заметке.
Примечание. Последнее решение не только наглядное, но и позволяет составлять аналогичные задачи учителю и учащимся. Парадокс не задача, не ее текст, а найденное решение реализует технологию развивающего обучения.
В завершение я хотел бы предостеречь моих читателей от типичного заблуждения относительно этих трех решений.
Многие ученики считают, что им нужно освоить, например, только прием из третьего решения, так как оно им нравится. Также есть учителя (и их не мало), которые считают, что им нужно рассказывать своим ученикам только третье решение, так как оно самое изящное, а о двух других решениях не стоит даже вспоминать.
Скажу сразу, что неправы все, как ученики так и учителя. Для того, чтобы стать профессионалом своего дела надо знать все решения данной задачи, даже если некоторые из них не являются рациональными в данном случае. Может случиться так, что прием третьего решение будет трудно реализовать в то время как приемы первого или второго решений останутся единственными из возможных.
Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 15 - Рисунок-ключ к решению текстовой задачи
Часть 16 - Угол между двумя плоскостями. Задание 16(С2)
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения
|
Процитировано 1 раз
Угол между двумя плоскостями. Задание 16(С2) |
В этой сообщении я расскажу об относительно новом приеме решения задачи на нахождение угла между плоскостями с помощью метода координат.
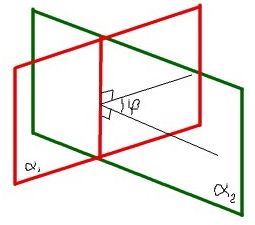
Как известно, две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величиной угла между плоскостями называется величина меньшего двугранного угла. Пусть φ - угол между этими двумя пересекающими плоскостями, а {a1; a2; a3} и {b1; b2; b3} - векторы, перпендикулярные плоскостям α1 и α2 соответственно. Эти векторы принято называть нормальными векторами к плоскостям α1 и α2. Тогда
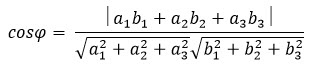
А теперь рассмотрим решение следующей задачи.
В правильной четырехугольной призме ABCDA1B1C1D1 со стороной основания 12 и высотой 21 на ребре AA1 взята точка М так, что AM = 8. На ребре BB1 взята точка K так, что B1К=8. Найдите угол между плоскостью D1MK и плоскостью CC1D1.
Выполним чертеж и введем введем систему координат так как на следующем рисунке.
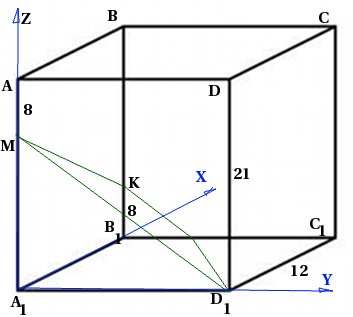
Эту задачу я позаимствовал на странице http://ege-ok.ru/2012/03/19/ugol-mezhdu-ploskostyami-metod-koordinat-zadanie-s2/. Однако далее мое решение будет резко отличаться от того, которое приведено там. Дело в том, что я буду использовать явно не традиционный координатный прием.
Нам нужно найти угол φ - угол между плоскостями D1MK и плоскостью CC1D1. Угол φ равен углу между нормалями к плоскостям D1MK и CC1D1.
Вектор {0; 1; 0} будет нормалью к плоскости CC1D1. Осталось найти нормаль к плоскости D1MK.
Пусть нормаль к плоскости D1MK имеет координаты {x; y; z}. Эта нормаль будет перпендикулярна векторам МК и МD.
Точки М, К и D имеют координаты (0; 0; 13), (12;0; 0 ) и (0; 12; 0) соответственно. Тогда вектор МК имеет координаты {12; 0; -13}, а вектор МD - {0; 12; -13}.
Так как вектор {x; y; z} перпендикулярен векторам МК и МD, то скалярное произведения вектора {x; y; z} и вектора МК равно 0. Точно также скалярное произведения вектора {x; y; z} и вектора МD равно 0. Поэтому
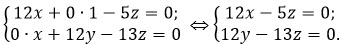
Положив z = 12 получим х = 5, у = 13.
Таким образом, векторы {0; 1; 0} и {5; 13; 12} будут перпендикулярны плоскостям CC1D1 и D1MK. Поэтому косинус угла между этими плоскостями мы найдем по формуле
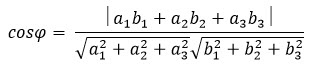
где a1 = 0; a2 = 1; a3 = 0 и b1 = 5; b2 = 13; b3 = 12.
Значит,
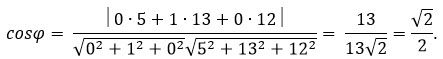
Поэтому φ = 45o.
Ответ: 45o.
"Плохое" решение Вы можете посмотреть и послушать (а лучше этого делать не стоит) на странице https://www.youtube.com/watch?v=4lqxVy2_tfE

Как известно, две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величиной угла между плоскостями называется величина меньшего двугранного угла. Пусть φ - угол между этими двумя пересекающими плоскостями, а {a1; a2; a3} и {b1; b2; b3} - векторы, перпендикулярные плоскостям α1 и α2 соответственно. Эти векторы принято называть нормальными векторами к плоскостям α1 и α2. Тогда
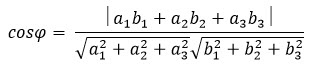
А теперь рассмотрим решение следующей задачи.
В правильной четырехугольной призме ABCDA1B1C1D1 со стороной основания 12 и высотой 21 на ребре AA1 взята точка М так, что AM = 8. На ребре BB1 взята точка K так, что B1К=8. Найдите угол между плоскостью D1MK и плоскостью CC1D1.
Выполним чертеж и введем введем систему координат так как на следующем рисунке.

Эту задачу я позаимствовал на странице http://ege-ok.ru/2012/03/19/ugol-mezhdu-ploskostyami-metod-koordinat-zadanie-s2/. Однако далее мое решение будет резко отличаться от того, которое приведено там. Дело в том, что я буду использовать явно не традиционный координатный прием.
Нам нужно найти угол φ - угол между плоскостями D1MK и плоскостью CC1D1. Угол φ равен углу между нормалями к плоскостям D1MK и CC1D1.
Вектор {0; 1; 0} будет нормалью к плоскости CC1D1. Осталось найти нормаль к плоскости D1MK.
Пусть нормаль к плоскости D1MK имеет координаты {x; y; z}. Эта нормаль будет перпендикулярна векторам МК и МD.
Точки М, К и D имеют координаты (0; 0; 13), (12;0; 0 ) и (0; 12; 0) соответственно. Тогда вектор МК имеет координаты {12; 0; -13}, а вектор МD - {0; 12; -13}.
Так как вектор {x; y; z} перпендикулярен векторам МК и МD, то скалярное произведения вектора {x; y; z} и вектора МК равно 0. Точно также скалярное произведения вектора {x; y; z} и вектора МD равно 0. Поэтому
Положив z = 12 получим х = 5, у = 13.
Таким образом, векторы {0; 1; 0} и {5; 13; 12} будут перпендикулярны плоскостям CC1D1 и D1MK. Поэтому косинус угла между этими плоскостями мы найдем по формуле
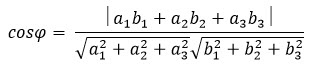
где a1 = 0; a2 = 1; a3 = 0 и b1 = 5; b2 = 13; b3 = 12.
Значит,
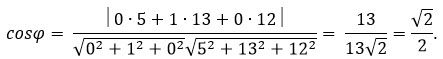
Поэтому φ = 45o.
Ответ: 45o.
"Плохое" решение Вы можете посмотреть и послушать (а лучше этого делать не стоит) на странице https://www.youtube.com/watch?v=4lqxVy2_tfE
Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 14 - Задача из рассказа «Репетитор» Антона Павловича Чехова
Часть 15 - Рисунок-ключ к решению текстовой задачи
Часть 16 - Угол между двумя плоскостями. Задание 16(С2)
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения
|
Как получить все и сразу |
Однажды мне пришлось подписаться на рассылку, выпуски которой присылались мне по мере их написания. Так мне показалось вначале, но потом в моей голове созрела мысль о том, что все выпуски рассылки уже давно готовы, но какой-то причине их автор высылает их по кускам. После получения очередной партии материала автор рассылки сообщал: "PS: завтра вышлю вторую партию уроков. Следите за почтой!". Сегодня одна партия, завтра другая и т. д.
Мне же захотелось получить их сразу все, а не тянуть время в течение нескольких дней, как этого хотел автор рассылки. Такова была задача. Я пытался решить ее по-разному, но не в коем случае не путем взлома сайта и других гадостей. Расскажу о решении этой задачи на примере сайта http://master-css.com/, который содержал (по моему подозрению) материалы уроков о верстке сайта. Я сначала подписался на эту рассылку и получил первое сообщение через электронную почту.
В этом письме мне предлагалось нажать на ссылку, ведущую не на файловый обменник сразу, а на страницу сайта http://master-css.com/. Почему не на сам файлов для его скачивания, а на сайт? Да ответ весьма простой. Автор рассылки повышал статистику посещаемости своего сайта. Для этого он в рассылке помещал некую "секретную" ссылку на страницу своего сайта, которая сообщала ее посетившему адрес для скачивания очередной порции уроков. Значит, подумал я, все эти "секретные" страницы уже созданы и автор сообщает их адреса мне "в час по чайной ложке", а не скопом сразу.
Вот как выглядело начало первого письма рассылки.

Еще раз повторюсь. Почему я их должен скачивать с некоторой страницы, а не сразу же после клика на эту ссылку? Ответ на этот вопрос я уже дал. Но перейдем к нашим баранам. Я кликнул на эту ссылку и попал на первую "секретную" страницу сайта http://master-css.com/. В конце этой страницы была

Но зачем мне нужно в течение нескольких дней ждать письма и получать эти ссылки? Нельзя ли получить эти ссылки сразу скопом и скачать все порции уроков?
Действительно, все "секретные" страницы уже созданы, но их адреса мне неизвестны. Значит, нужно как-то получить эти адреса. Наверное, для этого есть разные способы, и, среди них незаконные. Я же сторонник чистых методов, за которые не придется мне отвечать. Поэтому я стал искать инвариант, то единое, что повторяется на каждой из этих страниц.
Для этого я посмотрел начало "секретной" страницы.

Все просто, в начале каждой "секретной" странице должно быть слово "День".
А далее есть два элементарных способа выуживания адресов этих страниц. Рассмотрим первый способ.
На сайте http://master-css.com/ есть поиск. При этом этот поиск осуществляется только по всему этому сайту, а не по Интернету.
В окне этого поиска, как вы видите, я набрал слово "День" и вот только верхушка результата

В этом результате есть ссылки на все секретные страницы
http://master-css.com/page/den-1-nachinaems
http://master-css.com/page/den-2-shapka
http://master-css.com/page/den-3-content-1
http://master-css.com/page/d4-picter
http://master-css.com/page/d5-adapt
http://master-css.com/page/d5-adapt
http://master-css.com/page/d6-animate
С этих страниц я скачал все порции уроков. Вот и все - моя задача и решена. А как же задача автора сайта - повысить посещаемость своего сайта? Он тоже ее решил, ведь я посетил все эти страницы, но только за один день, как того не хотел их хозяин.
Теперь о том, как быть если на сайте http://master-css.com/ не оказалось бы поиска - это второй способ, о котором я говорил ранее. Здесь я буду краток. Во многих поисковиках есть так называемый расширенный поиск, который позволяет искать все страницы на сайте http://master-css.com/, на которых есть слово "День". Осуществив этот расширенный поиск я всегда смогу найти адреса этих секретных страниц.
Так, я смог получить все и сразу. Полученный опыт я использую не только для скачивания файлов с сайта, но и для поиска "закрытой" информации от "не избранных" посетителей на других сайтах.
Мне же захотелось получить их сразу все, а не тянуть время в течение нескольких дней, как этого хотел автор рассылки. Такова была задача. Я пытался решить ее по-разному, но не в коем случае не путем взлома сайта и других гадостей. Расскажу о решении этой задачи на примере сайта http://master-css.com/, который содержал (по моему подозрению) материалы уроков о верстке сайта. Я сначала подписался на эту рассылку и получил первое сообщение через электронную почту.
В этом письме мне предлагалось нажать на ссылку, ведущую не на файловый обменник сразу, а на страницу сайта http://master-css.com/. Почему не на сам файлов для его скачивания, а на сайт? Да ответ весьма простой. Автор рассылки повышал статистику посещаемости своего сайта. Для этого он в рассылке помещал некую "секретную" ссылку на страницу своего сайта, которая сообщала ее посетившему адрес для скачивания очередной порции уроков. Значит, подумал я, все эти "секретные" страницы уже созданы и автор сообщает их адреса мне "в час по чайной ложке", а не скопом сразу.
Вот как выглядело начало первого письма рассылки.

Еще раз повторюсь. Почему я их должен скачивать с некоторой страницы, а не сразу же после клика на эту ссылку? Ответ на этот вопрос я уже дал. Но перейдем к нашим баранам. Я кликнул на эту ссылку и попал на первую "секретную" страницу сайта http://master-css.com/. В конце этой страницы была

Но зачем мне нужно в течение нескольких дней ждать письма и получать эти ссылки? Нельзя ли получить эти ссылки сразу скопом и скачать все порции уроков?
Действительно, все "секретные" страницы уже созданы, но их адреса мне неизвестны. Значит, нужно как-то получить эти адреса. Наверное, для этого есть разные способы, и, среди них незаконные. Я же сторонник чистых методов, за которые не придется мне отвечать. Поэтому я стал искать инвариант, то единое, что повторяется на каждой из этих страниц.
Для этого я посмотрел начало "секретной" страницы.
Все просто, в начале каждой "секретной" странице должно быть слово "День".
А далее есть два элементарных способа выуживания адресов этих страниц. Рассмотрим первый способ.
На сайте http://master-css.com/ есть поиск. При этом этот поиск осуществляется только по всему этому сайту, а не по Интернету.

В окне этого поиска, как вы видите, я набрал слово "День" и вот только верхушка результата

В этом результате есть ссылки на все секретные страницы
http://master-css.com/page/den-1-nachinaems
http://master-css.com/page/den-2-shapka
http://master-css.com/page/den-3-content-1
http://master-css.com/page/d4-picter
http://master-css.com/page/d5-adapt
http://master-css.com/page/d5-adapt
http://master-css.com/page/d6-animate
С этих страниц я скачал все порции уроков. Вот и все - моя задача и решена. А как же задача автора сайта - повысить посещаемость своего сайта? Он тоже ее решил, ведь я посетил все эти страницы, но только за один день, как того не хотел их хозяин.
Теперь о том, как быть если на сайте http://master-css.com/ не оказалось бы поиска - это второй способ, о котором я говорил ранее. Здесь я буду краток. Во многих поисковиках есть так называемый расширенный поиск, который позволяет искать все страницы на сайте http://master-css.com/, на которых есть слово "День". Осуществив этот расширенный поиск я всегда смогу найти адреса этих секретных страниц.
Так, я смог получить все и сразу. Полученный опыт я использую не только для скачивания файлов с сайта, но и для поиска "закрытой" информации от "не избранных" посетителей на других сайтах.
|
ЕГЭ 2015. Задание № 20 (С5). Уравнение с параметром |
Бродя по бескрайним просторам Youtube нашел интересный видеоролик, который посвящен решению следующего уравнения с параметром.
Найти все значения параметра а, при которых уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 имеет ровно два корня.
Для этой задачи я нашел еще два решения, которые отличаются от того, которое привел автор упоминаемого ролика.
Решение I.
Так как левая часть уравнения четная функция, то уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 может иметь два решения только тогда, когда уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет единственное положительное решение либо тогда, когда уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет два корня разных знаков.
Рассмотри первый случай (уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет единственное положительное решение). В этом случае дискриминант этого уравнения равен нулю.
D = (2a - 1)2 - (3а2 - 2а) = 4а2 - 4a + 1 - а2 + 2а = а2 - 2a + 1 = (a - 1)2 = 0, a = 1. Тогда наше уравнение примет вид х2 - 2|х| + 1 = 0, (|х| - 1) = 0, |х| = 1, х = ±1. Действительно, наше уравнение имеет ровно два корня.
Во втором случае (уравнение t2 - (4а - 2)t + 3а2 - 2а = 0) необходимо и достаточно чтобы выполнялось неравенство 3а2 - 2а < 0, a(3a - 2) < 0. последнее неравенство имеет решение (0; 2/3).
nnfr? уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 имеет ровно два корня при а ∈ (0; 2/3) ∪ {1}.
Ответ: а ∈ (0; 2/3) ∪ {1}.
Решение II.
Решим уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0. Пусть |х| = t.
t2 - (4а - 2)t + 3а2 - 2а = 0
Нетрудно заметить, что свободный член этого уравнения равен 3а2 - 2а = а(3а - 2). При этом а + (3а - 2) = 4а - 2 - второй коэффициент с противоположным знаком. Значит, t = a или t = 3a - 2. Поэтому наше уравнение равносильно совокупности
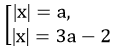
Понятно, что эта совокупность уравнений имеет ровно два решения лишь только в том случае, когда а = 3а - 2 и оба числа а и 3а - 2 положительны или а < 0 и 3а - 2 > 0 или а > 0 и 3а - 2 < 0. Во всех остальных случаях эта система либо не имеет решений, либо количество ее решений не равно двум.
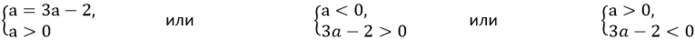
Первая система имеет решение а = 1. Вторая система не имеет решений, а решением третьей системы будет промежуток (0; 2/3). Поэтому решением совокупности будет множество (0; 2/3) ∪ {1}.
Ответ: а ∈ (0; 2/3) ∪ {1}.
Есть и третье решение нашего неравенства. Это решение я предлагаю посмотреть вот в этом видеоролике.
Это решение, которое предложил Никита мне понравилось. Оно наглядное. Однако есть один недостаток, решения предложенные мною требуют меньше времени. Но это только мое субъективное мнение.
Найти все значения параметра а, при которых уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 имеет ровно два корня.
Для этой задачи я нашел еще два решения, которые отличаются от того, которое привел автор упоминаемого ролика.
Решение I.
Так как левая часть уравнения четная функция, то уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 может иметь два решения только тогда, когда уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет единственное положительное решение либо тогда, когда уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет два корня разных знаков.
Рассмотри первый случай (уравнение t2 - (4а - 2)t + 3а2 - 2а = 0 имеет единственное положительное решение). В этом случае дискриминант этого уравнения равен нулю.
D = (2a - 1)2 - (3а2 - 2а) = 4а2 - 4a + 1 - а2 + 2а = а2 - 2a + 1 = (a - 1)2 = 0, a = 1. Тогда наше уравнение примет вид х2 - 2|х| + 1 = 0, (|х| - 1) = 0, |х| = 1, х = ±1. Действительно, наше уравнение имеет ровно два корня.
Во втором случае (уравнение t2 - (4а - 2)t + 3а2 - 2а = 0) необходимо и достаточно чтобы выполнялось неравенство 3а2 - 2а < 0, a(3a - 2) < 0. последнее неравенство имеет решение (0; 2/3).
nnfr? уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0 имеет ровно два корня при а ∈ (0; 2/3) ∪ {1}.
Ответ: а ∈ (0; 2/3) ∪ {1}.
Решение II.
Решим уравнение х2 - (4а - 2)|х| + 3а2 - 2а = 0. Пусть |х| = t.
t2 - (4а - 2)t + 3а2 - 2а = 0
Нетрудно заметить, что свободный член этого уравнения равен 3а2 - 2а = а(3а - 2). При этом а + (3а - 2) = 4а - 2 - второй коэффициент с противоположным знаком. Значит, t = a или t = 3a - 2. Поэтому наше уравнение равносильно совокупности
Понятно, что эта совокупность уравнений имеет ровно два решения лишь только в том случае, когда а = 3а - 2 и оба числа а и 3а - 2 положительны или а < 0 и 3а - 2 > 0 или а > 0 и 3а - 2 < 0. Во всех остальных случаях эта система либо не имеет решений, либо количество ее решений не равно двум.
Первая система имеет решение а = 1. Вторая система не имеет решений, а решением третьей системы будет промежуток (0; 2/3). Поэтому решением совокупности будет множество (0; 2/3) ∪ {1}.
Ответ: а ∈ (0; 2/3) ∪ {1}.
Есть и третье решение нашего неравенства. Это решение я предлагаю посмотреть вот в этом видеоролике.
Это решение, которое предложил Никита мне понравилось. Оно наглядное. Однако есть один недостаток, решения предложенные мною требуют меньше времени. Но это только мое субъективное мнение.
|









