-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
График нам поможет |
На сайте Ларина появился очередной вариант для подготовки к ЕГЭ. Меня заинтересовала задача 18 на уравнение с параметром. В частности меня интересует самое простое решение этой задачи, которое могут усвоить ученики не знакомые с премудростями дифференциального исчисления. Начало такого решения я подсмотрел у Виктора Осипова.

Ну а дальше, как говорится, мы пойдем своим путем.
Рассмотрим функцию p(t) = 3t² - 2t³ и построим ее график при помощи элементарных рассуждений.
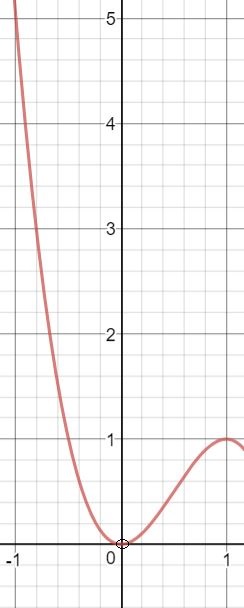
Понятно, что множеством значений этой функции является промежуток (0; 5] - множество значений параметра р, при которых данное уравнение имеет хотя бы одно решение.
Полное решение этого уравнения Виктором Осиповым и его конкурентом можно посмотреть ниже.

Ну а дальше, как говорится, мы пойдем своим путем.
Рассмотрим функцию p(t) = 3t² - 2t³ и построим ее график при помощи элементарных рассуждений.

Понятно, что множеством значений этой функции является промежуток (0; 5] - множество значений параметра р, при которых данное уравнение имеет хотя бы одно решение.
Полное решение этого уравнения Виктором Осиповым и его конкурентом можно посмотреть ниже.
|
|
Понравилось: 27 пользователям
Смотреть и видеть - это не одно и тоже |
Отслеживая некоторые материалы для подготовки школьников к сдаче ЕГЭ по математике я нашел два интересных решения следующей задачи.
Задача. Найти все значения параметра а, при которых уравнение
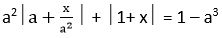
имеет не менее четырех различных решений, являющихся целыми числами?
Адреса этих решений я укажу в конце этой заметки. А пока мое решение этой задачи (задание 18 ЕГЭ по математике).

Воспользуемся следующей теоремой.
Теорема. |u| + |v| = u - v ⇔ {u ≥ 0, v≤ 0}.
В соответствие с этой теоремой данное неравенство равносильно системе
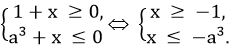
Поэтому последняя система, а значит, и исходное уравнение, будут иметь не менее четырех различных решений, являющихся целыми числами (-1, 0, 1 и 2 ) только при -а3 ≥ 2, a ≤ -21/3, т. е. при а ∈ (-∞; -21/3].
А вот и адреса адреса ранее упомянутых сообщений: https://www.youtube.com/watch?v=JWYbSlKc96c , https://www.youtube.com/watch?v=UZMVYUkFIII .
Решите еще одну задачу рассмотренным нами способом.
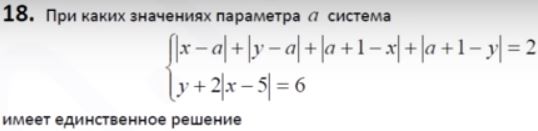
Задача. Найти все значения параметра а, при которых уравнение
имеет не менее четырех различных решений, являющихся целыми числами?
Адреса этих решений я укажу в конце этой заметки. А пока мое решение этой задачи (задание 18 ЕГЭ по математике).
Воспользуемся следующей теоремой.
Теорема. |u| + |v| = u - v ⇔ {u ≥ 0, v≤ 0}.
В соответствие с этой теоремой данное неравенство равносильно системе
Поэтому последняя система, а значит, и исходное уравнение, будут иметь не менее четырех различных решений, являющихся целыми числами (-1, 0, 1 и 2 ) только при -а3 ≥ 2, a ≤ -21/3, т. е. при а ∈ (-∞; -21/3].
А вот и адреса адреса ранее упомянутых сообщений: https://www.youtube.com/watch?v=JWYbSlKc96c , https://www.youtube.com/watch?v=UZMVYUkFIII .
Решите еще одну задачу рассмотренным нами способом.
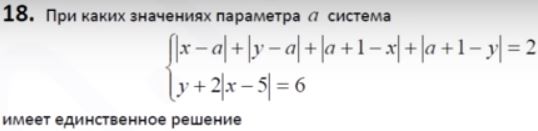
|
|
Сначала подумай, а потом пиши |
Бродя по просторам Интернета я нашел решение одной и то же задачи двумя людьми. Эти двое, как мне показалось, люди не обделенные умом. Однако они оба спешат и не пытаются найти оптимальные (рациональные) решения задач. Ну как школьники - "Я же решил первый, ответ же правильный. Не рационально, ну и что!"
Вот как решал эту задачу первый автор.
А вот как решил эту же задачу второй.
А есть ли у этой задачи другие решения, никто из них даже и не подумал. А жалко! Такие решения есть. Учителю было бы полезно предложить учащимся найти такие решения и выбрать из них самое рациональное.
Вот как решал эту задачу первый автор.
А вот как решил эту же задачу второй.
А есть ли у этой задачи другие решения, никто из них даже и не подумал. А жалко! Такие решения есть. Учителю было бы полезно предложить учащимся найти такие решения и выбрать из них самое рациональное.
|
|









