-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Три способа отбора корней тригонометрического уравнения |
На канале Валерия Волкова нашел интересный ролик, который фактически посвящен методическому вопросу. Вот он.
Тема решения тригонометрических уравнений и, в частности, отбора корней тригонометрического уравнения хорошо изложена в книге Прокофьева А.А., Корянова А.Г. "Тригонометрические уравнения: методы Решений и Отбор Корней", которую можно скачать у меня https://yadi.sk/i/4hLmFy4PxxPeg .
А вот еще один видеоролик, посвященный той же теме, но связанный с заданиями ЕГЭ по математике.
Тема решения тригонометрических уравнений и, в частности, отбора корней тригонометрического уравнения хорошо изложена в книге Прокофьева А.А., Корянова А.Г. "Тригонометрические уравнения: методы Решений и Отбор Корней", которую можно скачать у меня https://yadi.sk/i/4hLmFy4PxxPeg .
А вот еще один видеоролик, посвященный той же теме, но связанный с заданиями ЕГЭ по математике.
|
Процитировано 1 раз
Skype и другие его аналоги |
1. Skype (https://www.skype.com/ru/)- это незаменимый (пока еще) инструмент не только для общения в интернете, но и для проведения online занятий с учащимися. Для Skype созданы плагины. Их очень много. Для педагога незаменимым является Idroo - интерактивная доска.
2. Telegram - изобретение Павла Дурова (дин из создателей социальной сети «ВКонтакте»). Этот мессенджер набирает популярность.
Сайт программы https://telegram.org/ пока еще на английском. Но это не проблема, любой браузер его переведет на русский. Программа устанавливается на английском, но на youtube рассказано как сделать интерфейс на русском.
Есть две возможности использования Telegram: wеb вариант и вариант при помощи программы как на ПК, так и на других устройствах. Об этом рассказывается в следующих роликах.
Возможности Telegram можно увеличивать при помощи так называемых ботов.
3. Whatsapp - это еще один
4. Viber - очередной мессенджер.
список некоторых месседжеров можно посмотреть ниже.
5. Мессенджер Confide (текст)
Скачать: https://getconfide.com/download
6. Signal Private Messenger (текст, звонки). Этим мессенджером пользуется Эдвард Сноуден.
Скачать: https://whispersystems.org/
7. BitTorrent Bleep (текст, звонки)
Скачать: http://labs.bittorrent.com/bleep/
8. Jitsi (текст, звонки, видео)
На сайте http://keddr.com/2015/01/sravnenie-samyih-populyarnyih-messendzherov/ можно найти обзор многих мессенджеров.
Для любителей секретов можно использовать мессенджеры из следующего обзора.
2. Telegram - изобретение Павла Дурова (дин из создателей социальной сети «ВКонтакте»). Этот мессенджер набирает популярность.
Сайт программы https://telegram.org/ пока еще на английском. Но это не проблема, любой браузер его переведет на русский. Программа устанавливается на английском, но на youtube рассказано как сделать интерфейс на русском.
Есть две возможности использования Telegram: wеb вариант и вариант при помощи программы как на ПК, так и на других устройствах. Об этом рассказывается в следующих роликах.
Возможности Telegram можно увеличивать при помощи так называемых ботов.
3. Whatsapp - это еще один
4. Viber - очередной мессенджер.
список некоторых месседжеров можно посмотреть ниже.
5. Мессенджер Confide (текст)
Скачать: https://getconfide.com/download
6. Signal Private Messenger (текст, звонки). Этим мессенджером пользуется Эдвард Сноуден.
Скачать: https://whispersystems.org/
7. BitTorrent Bleep (текст, звонки)
Скачать: http://labs.bittorrent.com/bleep/
8. Jitsi (текст, звонки, видео)
На сайте http://keddr.com/2015/01/sravnenie-samyih-populyarnyih-messendzherov/ можно найти обзор многих мессенджеров.
Для любителей секретов можно использовать мессенджеры из следующего обзора.
|
Задачи на смеси и сплавы |
Весьма недурную схему решения задач на смеси придумал Павел Бердов.
|
|
Временная почта на mail.ru |
|
|
Понравилось: 1 пользователю
Как закачать любое видео в браузере Chrome |
Лучше чем в этом видео не расскажешь и не покажешь.
|
Множество значений функции |
Как правило в школьном курсе математики задач на эту тему очень мало. Да и те которые есть связаны с применением производной функции. Более менее хорошо разработана эта тема в книгах И.Х. Сивашинского. Этот автор предлагает изучать этот вопрос при помощи аппарата элементарной математики.
Здесь я предлагаю рассмотреть решение одной задачи по теме заголовка этого сообщения, которая предлагалась на вступительном экзамене в МГУ.
Задача. Найдите множество значений функции y =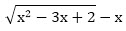 .
.
Рассмотрим далее цепочку равносильных уравнений.
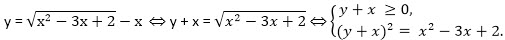
Решим второе уравнение последней системы относительно переменной х, используя только равносильные преобразования.
y2 + 2yx + x2 = x2 - 3x + 2, 2yx + 3x = 2 - y2, (2y + 3)x = 2 - y2 .
Если y = -1,5, то получаем неверное равенство 0х = -0,25. Значит, y не равно -1,5. Тогда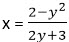 .
.
Так как х + y ≥ 0, то
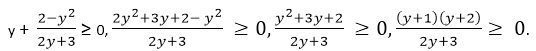 .
.
Решая последнее неравенство методом интервалов получаем y ∈ [-2; -3/2) U [-1; + ∞) - множество значений данной функции.
Здесь я предлагаю рассмотреть решение одной задачи по теме заголовка этого сообщения, которая предлагалась на вступительном экзамене в МГУ.
Задача. Найдите множество значений функции y =
Рассмотрим далее цепочку равносильных уравнений.
Решим второе уравнение последней системы относительно переменной х, используя только равносильные преобразования.
y2 + 2yx + x2 = x2 - 3x + 2, 2yx + 3x = 2 - y2, (2y + 3)x = 2 - y2 .
Если y = -1,5, то получаем неверное равенство 0х = -0,25. Значит, y не равно -1,5. Тогда
Так как х + y ≥ 0, то
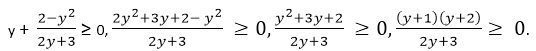 .
.Решая последнее неравенство методом интервалов получаем y ∈ [-2; -3/2) U [-1; + ∞) - множество значений данной функции.
|
|
Задача экзамена МГУ |
Мне попалась интересная задача.
Задача. Определите при каких значениях параметра а уравнение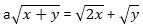 имеет единственное решение.
имеет единственное решение.
Решение. Понятно, что пара (0; 0) является решением данного уравнения при любом значении параметра а. Теперь нашу задачу можно переформулировать иначе.
При каких значениях параметра а уравнение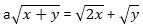 не имеет решений отличных от (0; 0).
не имеет решений отличных от (0; 0).
Так как (x; y) отлично от (0; 0), то данное уравнение можно преобразовать к виду и нужно определить при каких значениях параметра а это уравнение не имеет решений.
и нужно определить при каких значениях параметра а это уравнение не имеет решений.
Здесь есть прямой путь - использовать знание из теории функций с несколькими переменными и определить множество значений функции, расположенное в правой части последнего уравнения. но этот естественный путь для школьника не доступен. Однако рассказать ему об этом нужно.
Школьному учителю в данной ситуации остается только придумывать неестественные пути решения этой задачи. Например, такой способ.
Пусть , тогда
, тогда  , где 0 ≤ t ≤ 1 и получим уравнение
, где 0 ≤ t ≤ 1 и получим уравнение  . Это уравнение не имеет решений тогда и только тогда, когда а не принадлежит множествк значений функции из правой части уравнения.
. Это уравнение не имеет решений тогда и только тогда, когда а не принадлежит множествк значений функции из правой части уравнения.
Искомое множество значений функции находим методами теории функции одной переменной и получаем а ∈ (-∞ 1) ∪ (√3; +∞).
Задача для самостоятельного решения,/b>
Определите при каких значениях параметра а уравнение имеет единственное решение.
имеет единственное решение.
Задача. Определите при каких значениях параметра а уравнение
Решение. Понятно, что пара (0; 0) является решением данного уравнения при любом значении параметра а. Теперь нашу задачу можно переформулировать иначе.
При каких значениях параметра а уравнение
Так как (x; y) отлично от (0; 0), то данное уравнение можно преобразовать к виду
Здесь есть прямой путь - использовать знание из теории функций с несколькими переменными и определить множество значений функции, расположенное в правой части последнего уравнения. но этот естественный путь для школьника не доступен. Однако рассказать ему об этом нужно.
Школьному учителю в данной ситуации остается только придумывать неестественные пути решения этой задачи. Например, такой способ.
Пусть
Искомое множество значений функции находим методами теории функции одной переменной и получаем а ∈ (-∞ 1) ∪ (√3; +∞).
Определите при каких значениях параметра а уравнение
|
|
Задача №19 Досрочного ЕГЭ 2016 года |
 Всем известно, что марта 2016 года прошло досрочное ЕГЭ по математике. Это событие рассматривается многими как возможность предугадать темы последних задач ЕГЭ основного потока. Здесь я хочу рассмотреть решение задачи 18 (С6).
Всем известно, что марта 2016 года прошло досрочное ЕГЭ по математике. Это событие рассматривается многими как возможность предугадать темы последних задач ЕГЭ основного потока. Здесь я хочу рассмотреть решение задачи 18 (С6).Задача. Множество чисел назовем хорошим, если его можно разбить на два подмножества с одинаковой суммой чисел.
а) Является ли множество {100; 101; 102; ....; 199} хорошим?
б) Является ли множество {2; 4; 8; ....; 2100} хорошим?
в) Сколько хороших четырехэлементных подмножеств у множества {3; 4; 5; 6; 8; 10; 12}?
Решение
а) Так как (100 + 199) + (102 + 197) + ... + (148 + 151) = (101 + 198) + (103 + 196) + ... + (149 + 150), то {100; 199; 102; 197; ...; 148; 151} и {101; 198; 103; 196; 149; 150} разбиения множества {100; 101; 102; ....; 199} на два подмножества с одинаковой суммой чисел. Значит, множество {100; 101; 102; ....; 199} хорошее.
б) Так как 2 + 4 + 8 + ... + 299 < 2100 (докажите самостоятельно), то для любого разбиения множества {2; 4; 8; ....; 2100} на два подмножества только в одном из них содержится число 2100. Поэтому сумма чисел этого подмножества будет больше чем сумма чисел другого подмножества. Значит, {2; 4; 8; ....; 2100} не является хорошим.
в) Эту часть задания можно решать перебором. Сначала нужно доказать, что нет разбиений типа {a}, {d; c; d}. Затем следует перечислить разбиения типа {a; b} и {c; d}. Должен получиться ответ 8.
|
|
Понравилось: 1 пользователю
Типичная ошибка. Не переставляйте телегу с лошадью! |
Вот типичная ошибка, которая часто встречается в математических текстах.

Еще не факт, что если 2 - √5 является корнем квадратного уравнения с рациональными коэффициентами, то второй корень этого уравнения должен быть числом сопряженным, т. е. 2 + √5. Рассуждения автора этого текста являются правдоподобными, но не доказательными. Значит, приведенное решение - число 2 + √5 может быть не единственным, а только одним из возможных решений этой задачи (если есть другие).
Как же правильно решить эту задачу? Но это уже не тема этого сообщения.

Еще не факт, что если 2 - √5 является корнем квадратного уравнения с рациональными коэффициентами, то второй корень этого уравнения должен быть числом сопряженным, т. е. 2 + √5. Рассуждения автора этого текста являются правдоподобными, но не доказательными. Значит, приведенное решение - число 2 + √5 может быть не единственным, а только одним из возможных решений этой задачи (если есть другие).
Как же правильно решить эту задачу? Но это уже не тема этого сообщения.
|
|









