Эта заметка полностью посвящена решению следующей задачи ЕГЭ по математике.

Найти все значения параметра а при которых неравенство х² + 3|x - a| + a + x - 3 ≤ 0 имеет хотя бы одно неположительное решение.

Решение I. Существует весьма общий метод решения таких уравнений, неравенств и их систем, который известен в кругах профессиональных репетиторов по математике под названием "Координатно-параметрический метод". Этот метод хорошо описан в книге "Задачи с параметрами. Координатно-параметрический метод " В.П. Моденова. Скачать эту прекрасную книгу в электронном формате можно совершенно бесплатно в Интернете, например, по адресу http://mirknig.com/knigi/nauka_ucheba/1181707260-z...no-parametricheskiy-metod.html.
Решение нашей задачи этим методом я опубликую через некоторое время. А пока прочитайте мое Решение II и послушайте решение другого специалиста.

Решение II. Мне больше всего нравится другой способ (наверное, потому, что его придумал я :).

Найти все значения параметра а при которых неравенство х² + 3|x - a| + a + x - 3 ≤ 0 имеет хотя бы одно неположительное решение.

Все слагаемые, содержащие параметр а оставим в левой части, а остальные - перенесем в правую часть с противоположными знаками и получим неравенство 3|x - a| + a ≤ -х² - х + 3.

Как и в предыдущем случае решать будем графически. Построим "неподвижный" график y = -х² - х + 3 и зависящий от значения параметра а график ломанной y = 3|x - a| + a.


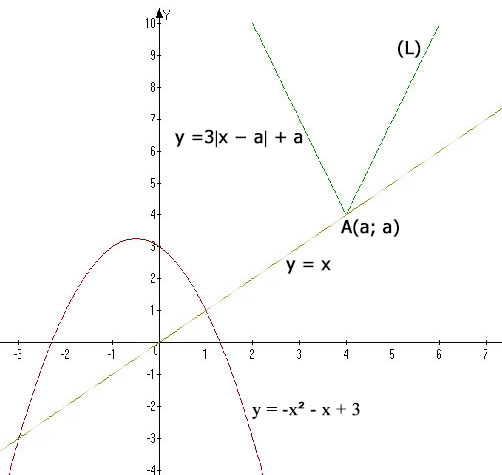
Расположение ломанной (L) зависит от значения параметра а. Однако в любом случае вершина А(a; a) лежит на прямой y = x.

Продолжим далее перевод нашей задачи на язык модели (графический язык). Нужно найти такие расположения ломанной (L), при которых эта ломанная будет иметь хотя бы одну точку с красной областью.



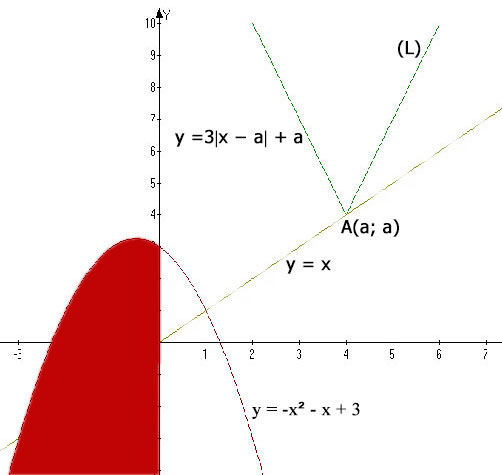
При этом нас устраивает даже такое положение ломанной (L), при котором она имеет только одну точку с красной областью. Поэтому если мы начнем опускать ломанную (L) вниз, то первая такая позиция будет (L₁) (см. рисунок ниже). В этом случае кривая (L₁) будет иметь единственную точку с красной областью - (0; 3).

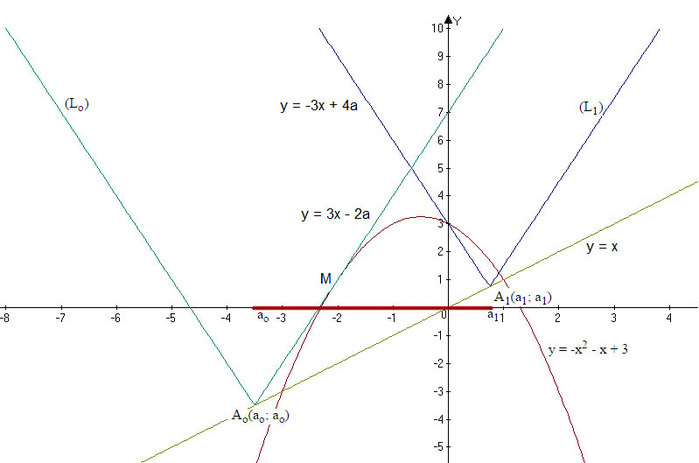
Найдем теперь другое крайнее положение ломанной (L) - нижнее. Это - кривая (L₀). Правое звено ломанной (L₀) луч y = 3x - 2a будет касаться красной области в точке М, абcцисса которой удовлетворяеет нашему неравенству.

Таким образом, если вершина ломанной (L) находится на отрезке А₀А₁, то кривая (L) будет иметь с красной областью хотя бы одну общую точку. Это и есть геометрическое решение нашей задачи.

Теперь остается найти алгебраическую интерпретацию этого решения, т. е. условие "вершина ломанной (L) находится на отрезке А₀А₁" выразить в виде алгебраического соотношения для параметра а. Нетрудно догадаться, что параметр а должен меняться от а₀ до а₁, т. е а ∈ [а₀; а₁].

Теперь остается только найти значения а₀ и а₁. Однако предварительно составим уравнения левой и правой ветви ломанной (L).

Для левой ветви ломанной (L) х ≤ а. Поэтому y = 3|x - a| + a = -3x + 3a + a = -3x + 4a. Для правой же ветви имеем х ≥ а; y = 3|x - a| + a = 3x - 3a + a = 3x - 2a.

Найдем теперь значение а₁. Левая ветвь ломанной (L₁) - луч y = -3x + 4a проходит через точку (0; 3), т. е. 3 = -3 ⋅ 0 + 4а, 4а = 3, а = 3/4. Значит, а₁= 3/4 = 0,75.

Теперь очередь за значением а₀. Найдем сначала координаты точки М. Луч y = 3x - 2a касается параболы y = -x₂ -x + 3. Это означает, что y' = (-x₂ - x + 3)' = -2x - 1 = 3, -2x = 4, x = -2 - абсцисса точки М. Подставим х = -2 в уравнение параболы и найдем значение ординаты точки М. y = -(-2)₂ - (-2) + 3 = -4 + 2 + 3 = 1.

Точка М(-2; 1) лежит на луче y = 3x - 2a. Из этого условия определим значение параметра а. 1 = 3 ⋅ (-2) - 2а, 2а = -7, а = -3,5. Значит, а₀ = -3,5.

Ответ: a ∈ [-3,5; 0,75].

Решение III. Предыдущие два решения я придумал после того как посмотрел следующий видеоролик с оригинальным решением. Вообще должен отметить, что на этом канале приведены очень толковые решения заданий тестов ЕГЭ (особенно тех, в которых нужная высокая математическая грамотность).

Пример формирования эмпирического мышления

Эмпирическое (опытное) мышление и познание представляет собой деятельность, в основе которой преобладает живое, непосредственное созерцание объекта.

Оно прежде всего сохраняет свою связь с восприятием. В ходе эмпирического мышления познаваемый объект отражается со стороны его внешних связей и свойств. В процессе познания познающий ориентируется на внешние условия существования объекта и на то содержание в нем, которое прямо доступно восприятию и наблюдению.

Результатом эмпирического мышления выступает знание непосредственного в действительности. В таком знании отражаются внешние сходные черты познаваемых объектов, но не его внутренняя сущность скрытая от внешнего созерцания.

Рассмотрим пример из обычной практики преподавания математики в средней общеобразовательной школе.

Решить уравнение



Эта задача кочует из одного методического пособия в другое. В прекрасном сборнике задач [1] предлагается такое решение.

Поделим числитель и знаменатель дроби, расположенной в левой части уравнения на х², конечно, предварительно проверив число 0 на роль корня уравнения. После выполнения этой операции получим






Введем теперь обозначение х + 1/x = y, тогда наше последнее уравнение примет вид




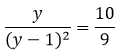
10y² - 20y +10 = 9y, 10y² - 29y +10 = 0, D = 29² - 4 ⋅ 10 ⋅ 10 = 841 - 400 = 441 = 21², y₁ = 0,8; y₂ = 2,5.


Если y₁ = 0,8; х + 1/x =2/5; 5x² - 2x + 5 = 0. Это уравнение не имеет действительных корней.

Если y₂ = 2,5; х + 1/x =5/2; 2x² - 5x + 2 = 0; D = 25 - 4 ⋅ 2 ⋅ 2 = 3₂, x₁ =1/2; x₂ = 2.

Ответ: 1/2; 2.

Это типичный пример формирования эмпирического мышления учащихся, т . к. практика преподавания математики в современной школе предполагает после такого решения этого уравнения рассмотренным выше способом решение еще нескольких таких же аналогичных уравнений для того, чтобы учащиеся прочно овладели соответствующими навыками. Это и называют в современной школе закреплением.

Ни в пособии [1], ни в других пособиях, содержащих рассмотренное выше уравнение (или аналогичное) не проводится анализа решения.

Действительно, почему надо делить числитель и знаменатель дроби из левой части данного уравнения на х². Это что новый метод? А может ничего нового здесь нет? А как рассмотренный прием (деления на х²) согласуется с ранее приобретенными знаниями учащихся? Может быть мы уже применяли этот способ?

Все эти вопросы остаются без ответа. Нет даже попытки авторами методических пособий сформулировать эти вопросы. Типичный признак эмпирического преподавания математики: запомни, повтори, примени много много раз. Так и здесь.

В терминах классической методики преподавания математика здесь мы наблюдаем нарушение принципа научности. Действительно, НАУКА - это сфера человеческой деятельности, функция которой — выработка и теоретическая систематизация объективных знаний о действительности. Поэтому не ясно к какой системе знаний относятся метод решения этого уравнения.

Наука охватывает не только деятельность по получению нового знания, но и результаты этой деятельности — систему научных знаний, которая лежит в основе научной картины мира. Поэтому любые новые знания должны находиться в определенной связи с ранее полученной информацией или относится к новому разделу науки.

Другими словами, наше уравнение и его методы решения должны входить в систему знаний об уравнениях вообще и в систему знаний о некоторых, ранее изученных типах уравнений, так как только в этом случае образуется совокупность элементов, взаимосвязанных друг с другом и таким образом образующих определенную научно организованную целостность.

О том, что автор, предложивший этот метод решения нашего уравнения открыл нечто новое, еще неизвестное другим трудно себе представить. Наверное его "метод" - это нечто вырванное из контекста ранее известного.

Такой рецептурный подход преподавания математики изжил себя уже давно. Действительно, что будет, если так мы будем поступать со всеми уравнениями - предлагать для каждого из них "свой" рецепт решения. Выдержит ли память у учеников? Ведь она не безгранична! Сколько же нужно при этом тупо, механически запомнить и сколько нужно потратить времени на соответствующую тренировку чтобы как-то усвоить эти многочисленные доморощенные "методы".

Думаю, что поставленные мной вопросы говорят о том, что так преподавать математику сегодня нельзя. Нельзя даже описывать решения известных задач. В этом плане стоит поучиться у Л. Эйлера, который значительную часть своих статей посвящал описанию того как он получал решения научных вопросов и тому с какими известными задачами связано его решение.

В этой заметке я только критикую сложившуюся практику преподавания математики и не даю ответа на вопрос о том, как же надо преподавать математику, даже на примере решения на уроке рассмотренного выше уравнения. Это и будет целью моих следующих заметок, но уже закрытого типа.

Литература

1. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учебн. пособие для 10 кл. сред. шк. - М., Просвещение, 1989.

Как стало недавно известно, в 2014-2015 учебном году планируется проведение двух отдельных экзаменов ЕГЭ – базового и профильного – по КИМ, разработанным в соответствие с разными спецификациями.

При этом баллы, полученные на базовом ЕГЭ по математике, не будут переводятся в стобалльную шкалу и не дадут школьнику возможности участия в конкурсе на поступление в вузы.

Результаты же профильного ЕГЭ по математике переводятся в стобалльную шкалу и могут быть представлены абитуриентом на на конкурс для поступления в вуз.

И вот читая очередной шедевр российской методической мысли, а если быть точнее демовариант базового уровня ЕГЭ по математике я обнаружил очень интересное задание предназначенное выпускникам 11-летней школы.


Поставлю себя на место среднего, даже двоечника по математике и начну решать это задание опираясь на свои скудные знания и навыки.

Итак, каким же может быть рост ребенка. 32 км, 30 м или 0,2 мм, конечно же никак нет. Даже первокласснику это понятно. Так что остается выбрать ответ 110 см. Вообще стоило ли учить ученика до 16-17 лет, чтобы проверять у него наличие таких знаний. Думаю, что такие задания стыдно задавать даже дебилам.

Каково же возможное значение толщины листа бумаги? Опять перебираю предложенные ответы и, снова надо быть тупым бараном, чтобы не увидеть правильный ответ - 0,2 мм. Чудны дела твои Министерство Образования и Науки РФ! Тем кто составлял такие задания место явно не там, где они сейчас.

Пойдем дальше. Чему же равна длина автобусного маршрута. Может быть 30 м, 0,2 мм или 110 см? Тут снова догадаться нетрудно - 32 км. Да что-то непохоже на правду. Может быть составитель этого задания дальше Москвы других городов и не знает! Тогда ему самое время отвечать на такие вопросы.

Относительно высота жилого дома и к бабке ходить не надо - свободный ответ только 30 м.

Что я почувствовал на месте того ученика, которому предлагаются такие задания? Догадаться, наверное, нетрудно. А если составители этого задания не смогли сообразить, то для них, особо одаренных, напишу. Появляется желание не продолжать дальше учиться, а то как тот Иванушка станешь не козленком, а уже полным идиотом.

Однако хочу быть справедливым. Министерство Образования и Науки РФ не одиноко в своих делах. В Казахстане дела обстоят не лучше. Там еще не отказались от тестовых заданий с пятью ответами для выбора только одного правильного среди них. Да и содержание этих тестовых заданий - такой же педагогический брак. Об этом я уже писал в заметке ВЕСЕЛИСЬ, СТРАНА ДУРАКОВ, И НЕ О ЧЕМ НЕ ДУМАЙ!

Задача №18. В городе Z в 2013 году мальчиков родилось больше, чем девочек. Мальчиков чаще всего называли Андрей, а девочек – Мария. Выберите утверждения, которые следуют из приведённых данных. В 2013 году в городе Z:

1) Марий родилось больше, чем Светлан.
2) Николаев родилось больше, чем Аристархов.
3) Хотя бы одного из родившихся мальчиков назвали Андреем.
4) Андреев больше, чем Марий.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решение. Предлагаю сначала зафиксировать все то, что нам известно из условия задачи:

I. Мальчиков родилось больше, чем девочек.
II. Мальчиков чаще всего называли Андрей.
III. Девочек чаще всего называли Мария.

Теперь поочередно будем исследовать истинность суждений в вопросе этой задачи.

1) Марий родилось больше, чем Светлан. Это суждение будем сравнивать с суждениями I, II и III. Суждение 1) и I ничего общего не имеют, т. е. из I ни как не следует 1). Точно также 1) и II ни находятся во взаимной зависимости. А вот из III (Девочек чаще всего называли Мария) явно следует, что Марий было больше, чем девочек с другими именами, т. е. Марий было больше чем, Светлан. Значит, суждение 1) следует из суждения III и, значит, из совокупности всех суждений I, II и III.

Суждение 2) Николаев родилось больше, чем Аристархов. никак ни следует из каждого из суждений I, II, III их пар и всех суждений I, II, III одновременно.

Суждение 3) Хотя бы одного из родившихся мальчиков назвали Андреем. следует из суждений I и II. Здесь фактически нужно доказать два простых суждения: "Родился хотя бы один мальчик" и "Среди всех мальчиков был мальчик с именем Андрей".

Раз I. Мальчиков родилось больше, чем девочек, то хотя бы один мальчик родился на свет. Так как II. Мальчиков чаще всего называли Андрей., то то хотя бы одного родившегося мальчика (а он, как было доказано ранее, точно родился) назвали Андреем.

Суждение 4) Андреев больше, чем Марий. Ни как не следует ни из одного из суждений I, II и III. Это суждение также не следует из пар суждений I и II, I и III, II и III. Также суждение 4) не следует из совокупности всех суждений I, II и III.

Итак, из суждений 1), 2), 3) и 4) только 1) и 3) следуют из условий I, II и III.

Ответ: 13. Как всегда мне хотелось бы высказать свое мнение о включении этого задания в вариант ЕГЭ.

Это задание никакого отношения к школьному курсу математики не имеет. Скорее свего это упражнение можно отнести к курсу формальной (аристотелевой) логики, которая, к сожалению, не изучается в массовой общеобразовательной школе. Справедливости ради, следует отметить, что это задание можно решить, опираясь на обычную, житейскую логику мышления. Однако это никак не оправдывает ее включение в тест ЕГЭ по МАТЕМАТИКЕ.


Дело в том, что любое задание, не обязательно математическое, надо выполнять опираясь на соответствующий теоретический материал. Выпускник обычной школы в данном случае этого не может сделать, а значит, он вынужден решать ее с применением так называемых житейских соображений. Такое решение никаких знаний и умений, в том числе и математических, не проверяет.

Место этой задачи, в лучшем случае, - кружок любителей порассуждать в младших классах. О таких задачах в тестах НЕТ (аналог ЕГЭ в Казахстане) я уже писал в своем блоге в сообщении "Задача о дележе наследства" - http://www.liveinternet.ru/users/kifar/post214470609/.

Рассмотри решение логической задачи из базового демоварианта тестов ЕГЭ-2015.

В городе Z в 2013 году мальчиков родилось больше, чем девочек. Мальчиков
чаще всего называли Андрей, а девочек – Мария. Выберите утверждения, которые следуют из приведённых данных. В 2013 году в городе Z:

1) Марий родилось больше, чем Светлан.
2) Николаев родилось больше, чем Аристархов.
3) Хотя бы одного из родившихся мальчиков назвали Андреем.
4) Андреев больше, чем Марий.

В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решение. Предлагаю сначала зафиксировать все то, что нам известно из условия задачи:

I. Мальчиков родилось больше, чем девочек.
II. Мальчиков чаще всего называли Андрей.
III. Девочек чаще всего называли Мария.

Теперь поочередно будем исследовать истинность суждений в вопросе этой задачи.

1) Марий родилось больше, чем Светлан. Это суждение будем сравнивать с суждениями I, II и III. Суждение 1) и I ничего общего не имеют, т. е. из I ни как не следует 1). Точно также 1) и II ни находятся во взаимной зависимости. А вот из III (Девочек чаще всего называли Мария) явно следует, что Марий было больше, чем девочек с другими именами, т. е. Марий было больше чем, Светлан. Значит, суждение 1) следует из суждения III и, значит, из совокупности всех суждений I, II и III.

Суждение 2) Николаев родилось больше, чем Аристархов никак ни следует из каждого из суждений I, II, III их пар и всех суждений I, II, III одновременно.

Суждение 3) Хотя бы одного из родившихся мальчиков назвали Андреем. следует из суждений I и II. Здесь фактически нужно доказать два простых суждения: "Родился хотя бы один мальчик" и "Среди всех мальчиков был мальчик с именем Андрей".

Раз I. Мальчиков родилось больше, чем девочек, то хотя бы один мальчик родился на свет. Так как II. Мальчиков чаще всего называли Андрей., то то хотя бы одного родившегося мальчика (а он, как было доказано ранее, точно родился) назвали Андреем.

Суждение 4) Андреев больше, чем Марий. Ни как не следует ни из одного из суждений I, II и III. Это суждение также не следует из пар суждений I и II, I и III, II и III. Также суждение 4) не следует из совокупности всех суждений I, II и III.

Итак, из суждений 1), 2), 3) и 4) только 1) и 3) следуют из условий I, II и III.

Ответ: 13.

Как всегда мне хотелось бы высказать свое мнение о включении этого задания в вариант ЕГЭ.

Это задание никакого отношения к школьному курсу математики не имеет. Скорее всего это упражнение можно отнести к курсу формальной (аристотелевой) логики, которая, к сожалению, не изучается в массовой общеобразовательной школе. Справедливости ради, следует отметить, что это задание можно решить, опираясь на обычную, житейскую логику мышления. Однако это никак не оправдывает ее включение в тест ЕГЭ по МАТЕМАТИКЕ.

Дело в том, что любое задание, не обязательно математическое, надо выполнять опираясь на соответствующий теоретический материал. Выпускник обычной школы в данном случае этого не может сделать, а значит, он вынужден решать ее с применением так называемых житейских соображений. Такое решение никаких знаний и умений, в том числе и математических, не проверяет.

Место этой задачи, в лучшем случае, - кружок любителей порассуждать в младших классах. О таких задачах в тестах НЕТ (аналог ЕГЭ в Казахстане) я уже писал в своем блоге в сообщении "Задача о дележе наследства"
- http://www.liveinternet.ru/users/kifar/post214470609/.

На сайте
http://egeent.ucoz.ru/publ/podgotovka_k_egeh_i_ent...ematike_v_2015_godu/24-1-0-247 я уже подробно писал о том, что в 2014-2015 о том, что в новом учебном году произошли достаточно серьезные изменения в содержании и форме тестов экзамена ЕГЭ по математике. Эти изменения четко и однозначно отражены в базовом и профильном демовариантах ЕГЭ для 2015 года, с которыми можно познакомиться, скачав их здесь и тут.

А сейчас приступим к детальному разбору содержания этих демовариантов в серии выпусков моей рассылки.

Задание 19. Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.

Решение 1. 578. Действительно, 5 + 7 + 8 = 20, 5² + 7² + 8² = 25 + 49 + 64 = 138. У числа 138 сумма цифр равна 12. Так как 12 делится на 3, но не делится на 9, то сумма квадратов цифр числа 578 делится на 3, но не делится на 9.

Ответ: 578.

Это решение вполне допустимо и с точки зрения математики здесь все в порядке, но не понятно, откуда взялось число 578, а не 758. Дело в том, что в условии сказано "Приведите пример", а не "найдите ...".

Решение 2. Пусть а, b и с - цифры искомого трехзначного числа. Так как а + b + с = 20, 20 = 18 + 2, то сумма остатков от деления цифр а, b и с на 3 может быть равна 2, 5, так как сумма этих остатков тоже должна при делении на 3 давать остаток 2.

Если то сумма остатков от деления цифр а, b и с на 3 равна 2, то может быть два варианта:
а) две цифры делятся на 3, а треться при делении дает остаток 2. Этот случай нам не подходит, так как сумма квадратов цифр искомого числа при делении на 3 дает тот же остаток что и число 4, т.е. 1.
б) одна цифра делятся на на три, а две другие при делении дают остатки 3 по 1. Этот случай нам также не подходит, так как сумма квадратов цифр искомого числа при делении на 3 дает тот же остаток что и число 1² + 1², т.е. 2.

Если сумма остатков от деления цифр а, b и с на 3 равна 5, то 5 = 2 + 2 + 1 и другой возможности представления числа 5 в виде суммы остатков от деления цифр а, b и с на 3 с точностью до порядка следования слагаемых нет.

Значит, а + b + с = 3x + 1 + 3y + 2 + 3z + 2 = 20. При этом x ≤ 3, a y ≤ 2, z ≤ 2, так 3x + 1, 3y + 2 и 3z + 2 - цифры.

3(x + y + z) = 15,
x + y + z = 5.

Число 5 можно представить в вмде суммы трех чисел x, y и z (x ≤ 3, a y ≤ 2 и z ≤ 2) только только такими способоми: x = 1, y = z = 2 или y = 1, x = z = 2 или z = 1, y = x = 2.

Если x = 1, y = z = 2, то цифры искомого числа равны 3x + 1 = 4, 3y + 2 = 3z + 2 = 8, но тогда 4² + 8² + 8² = 144 - делится на 9.

Если y = 1, x = z = 2 или z = 1, y = x = 2, то цифры искомого числа равны 7, 5 и 8. При этом цифры 7, 5 и 8 удовлетворяют условию задачи и из этих цифр можно составить шесть чисел: 578, 587, 758, 785, 857, 875.

Ответ: 578 или 587 или 758 или 785 или 857 или 875.

Решение 3. Пусть а, b и с - цифры искомого трехзначного числа. Тогда а + b + с = 20.

Наименьшее из трех цифр а, b и с не может равняться 1, так как в противном случае сумма двух других будет равна 19, а для цифр это невозможно.

Представим число 20 в виде суммы трех слагаемых от 2 до 9 с точностью до порядка следования слагаемых.

20 = 2 + 9 + 9 = 3 + 9 + 8 = 4 + 9 + 7 = 4 + 8 + 8 = 5 + 9 + 6 = 5 + 8 + 7. Других способов представления числа 20 нет.

Условию "сумма квадратов цифр делится на 3, но не делится на 9" удовлетворяет только тройка цифр 5, 7 и 8. Из этих цифр можно составить шесть чисел: 578, 587, 758, 785, 857, 875.

Ответ: 578 или 587 или 758 или 785 или 857 или 875.

А теперь несколько слов о критериях оценки этого тестового задания ЕГЭ.

При любом их трех правильных решений, приведенных, например, выше, ученик получает одно и тоже количество баллов. Однако было бы справедливо, если ученик, который привел первое решение должен получить меньшее число баллов, по сравнению с теми, кто решил вторым и третьим способами. Однако этого не произойдет. Так что критерии оценок тестов ЕГЭ пока еще не совершенны.

Да достигнуть этого совершенства, на мой взгляд, принципиально невозможно, так как человеческий способ оценки школьников пока еще не превзошел никакой автомат или компьютер и так будет происходить еще очень долго.