я тут начал писать билеты к колку по алгебре...
их 28 а я пока осилил токо 3))))
Билет 1Определение комплексного числа. Действия с комплексными числами: сложение, умножение, сопряжение, деление. Алгебраическая форма комлексного числа. Тригонометрическая фора комплексного числа. Умножение комплексных чисел в тригонометрической форме. Формула Муавра.Определение комлексного числа.Это расширение множества вещественных чисел (С). Любое комплексное число может быть представленно в виде суммы x + iy, где x и y - вещественные числа, i - мнимая единица, то есть одно из чисел, удоволетворяющих уравнению i^2 = - 1.
Действия с комплексными числами.Формально, комплексное число z - это пара чисел (x,y) с которыми можно производить операции сложения и умножения таким способом:
сложение:(x,y) + (x',y') = (x + x', y + y')
умножение:(x,y)*(x',y') = (xx'- yy', xy' + yx')
сопряжение: Свойства сопряженных чисел
деление:
Если делимое и делитель даны не в тригонометрической форме, а в виде
a1 +
b1i
и
a2 +
b2i
, то выражая в формуле (9) модули и аргументы через
a1,
a2,
b1,
b2, получим следующее выражение для частного:
Алгебраическая форма комлексного числа.
Запись комплексного числа
z в виде
x +
iy,
, называется
алгебраической формой комплексного числа.
Тригонометрическая форма комплексного числа.
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент 
(
, 
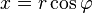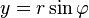), то комплексное число z можно записать в тригонометрической форме
.
- Умножение комплексных чисел в тригонометрической форме.
Пусть теперь нам даны комплексные числа
и
. Давайте их
перемножим:
Формула Муавра.
Формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
![z^n=[r(\cos \varphi +i\sin \varphi)]^n =<br />
r^n(\cos n\varphi +i\sin n\varphi)](http://upload.wikimedia.org/math/1/a/b/1abd6bc290224e267b17c39c6be66ed0.png)
,
где r — модуль, а — аргумент комплексного числа.
Или словами - при умножении комплексных чисел их модули перемножаются а аргументы складываются.
