Ответы не прозрачны

Многие тестовые задания ЕНТ по математике составлены так, что найти правильный ответ - дело пустяковое. Это можно сделать без особых затруднений. Например, подставь все ответы по очереди в данное уравнение или систему уравнений и за 1-2 минуты правильный ответ обязательно будет найден. Такие задачи даже решать не хочется, методы их решения, а точнее подбора правильного ответа очевидны.

Однако в тестах ЕНТ встречаются и такие задания, которые не допускают таких решений. При этом как не прячь правильный ответ среди других, все равно есть возможность его можно обнаружить. Важно, чтобы это можно было сделать очень быстро и легко. Для этого надо знать некоторые профессиональные приемы этой деятельности. Такие приемы не возникают сами по себе. Их нужно изучать систематически. Вот один тип таких заданий и приемы его решения.

Пусть (х; у) - решение системы найдите х + 2у.

А) 8         В) 0         С) 5         D) -8         E) 6        


Нетрудно заметить, что х > 0, у > 0 и х > у. Поэтому ответы В) и D) следует отбросить. Так как х + 2у > х + у, то следует отбросить и ответ С). Осталось два ответа А) и Е).

Можно предположить, что ответами будут целые положительные числа квадратные корни из которых тоже целые положительные числа. Значит, х и у квадраты целых чисел, х > y и х + у = 5. Такие числа 4 и 1. можно проверить, что числа 4 и 1 - решения данной системы уравнений. Поэтому х + 2у = 6. Правильный ответ Е).

Вот еще два таких тестовых задания, которые предлагаю читателям решить самостоятельно.


1. Найдите значение х + у, где (х; у) - решение системы: .

А) 4         В) 81         С) 20         D) 52         E) 34        

2. Найдите значение , где (х; у) - решение системы: .

А) 1         В) 3         С) 5         D) 4         E) 2        

О решении одной системы

В этом сообщении хотел бы рассказать о одном красивом решении тестового задания ЕНТ. В сборниках для подготовки к ЕНТ, к сожалению, очень мало таких красивых задач.Такие задачи, а если быть точнее, тестовые задания с несколькими ответами для выбора одного правильного среди них позволяют развивать интуицию и исследовательские навыки учащихся. Как говорится, на безрыбье и рак рыба. Педагогический брак иногда можно превратить в его противоположность.

Решите систему уравнений: . Найдите х₁ + х₂.
А) 32         В) 16        С) 24        D) 18        Е) 20       


Решение. Первое уравнение преобразуется к виду ху = 36. Мне все равно что будет на месте 36, важен вид этого уравнения. Второе уравнение заменится уравнением х + у = 20.

Поэтому данная система будет равносильна системе . Как известно, решениями такой системы являются пары числе (х₁; х₂) и (х₂; х₁), где х₁ и х₂ решения квадратного уравнения t² - 20t + 36 =0.

Однако нам не нужны сами решения этой системы, а нужно вычислить х₁ + х₂. По теореме Виета х₁ + х₂ = 20.

Ответ: 20.

Третий сорт - не брак

Читая последний сборник для подготовки к очередному ЕНТ по математике не перестаю удивляться тому, как много в этом опусе педагогического брака, свидетельствующего о том, какая низкая квалификация у ее составителей.

Все бы ничего. Много у нас еще выпускается, да и выпускалось и, наверное, будет выпускаться педагогический мусор, но этот сборник является лицом нашего государства. От его качества зависит то, как другие станут оценивать уровень образования в нашей стране.

Мне стыдно за свое государство, руководители которого говорят пышные фразы о том, как они заботятся об образовании подрастающего поколения и доказывают правдивость своих речений подобными вещами как содержание ЕНТ.

Приведу очередной пример.

Решите неравенство log_2x+1(5 -2x) < 1.

A) (-1; 0)        B) (2,5; +∞)       C) (-1,5; 2,5)        D) (-∞; 2,5)        E) (0; 1)

Ответы В) и D) следует сразу же отбросить, так как при достаточно больших х выражение 5 - 2х станет отрицательным, а при очень малых значениях х основание логарифма будет отрицательным.

При х = -0,5 (-0,5 входит в ответы А) и С))основание логарифма примет значение 1. Что также недопустимо. Остается единственный ответ Е).

При выполнении этого задания тестируемому приходится хоть что-то делать (выполнять подстановку значений переменной в данное выражение, вспоминать определение и свойства логарифма и т. п.). Но ведь есть в сборнике и такие задания, которые решаются буквально одним взглядом.


Правильный ответ Е). Остальные ответы не могут быть правильными, так как содержат отрицательные значения для переменной х. При отрицательном х данное неравенство не имеет смысла.

Вот таков он, уровень выпускника средней школы Казахстана.

Лап-табу-дибу-ду-дааай ответ на тест ЕНТ

Всем известно, что как не совершенствуй паровоз, а его коэффициент полезного действия не превышает 14-15 %. Так и с тестами с несколькими ответами для выбора одного из них в качестве правильного. Как их не совершенствуй, все равно будут дырки для быстрого выбора правильного ответа среди предложенных.

Казалось бы прекрасно следующее тестовое задание.

Известно, что 3а² = 2b³. Число а увеличили в 2 раза. Во сколько раз увеличилось число b.

А) 64        B) √4        C) 4        D) 16        E)

Все хорошо, есть исследование, вызывает интерес, увлекает и т. п. Но есть только одна Ахиллесова пята, которая сводит на нет все достоинства этого упражнения - ответы. Действительно, наличие ответов подсказывает, что только один серди них правильный. Да и он не зависит от значений а и b. Поэтому зададим, например, сначала а = 1 и подсчитаем b. Затем положим а = 2 (то есть увеличим а в два раз) и вычислим соответствующее значение b. первоначальное значение b разделим на его второе значение и получим искомый ответ.

Вот реализация этого плана.
а = 1: 3 = 2b³, b³ = 1,5; b =
a = 2 (a увеличим а в два раз): 12 = 2b³, b³ = 1,5; b = .

: = .

Вот и столь не долгожданный ответ. Наличие независящих от параметров а и b навело нас на мысль, что искомый ответ от этих параметров не зависит. А дальше дело техники.

Вот еще один шедевр того же типа для самостоятельного решения.


Если 0 < a < 1 и b > 1, то какое из перечисленных чисел самое маленькое

А) а + b        B) a : b        C) a        D) b        E) ab

Купил очередной сборник тестов для подготовки к ЕНТ (Казахстан). Решил полистать, есть ли что-нибудь нового в этом году. И нашел такое, что привело меня в состояние истерического хохота. Невольно вспомнил выражение "Веселись, страна дураков, и не о чем не думай!" из произведения братьев Стругацких.

Действительно, кто только не критиковал систему аттестации ЕНТ в Казахстане. Отрицательно отзывались учителя, методисты, ученные, журналисты, депутаты парламента, а воз и поныне все там же (в болоте педагогического невежества) в течение более 20 лет. Не буду голословным приведу пример тестового задания для выпускника средней школы, который, конечно же, собирается стать представителем элиты нашей страны.

Значение выражения 541 ⋅ 1 + 459 : 1 равно

А) 542         В) 1000        С) 459         D) 990        Е) 460


Не знаю как у Вас, а меня создалось впечатление, что выпускникам средних школ Казахстана, которым предлагаются такие задания место не в рядах интеллектуальной элиты, а в другом месте. Кого же мы хотим видеть в выпускнике средней школы?

А вот еще один шедевр из этого же сборника.

Если треугольник прямоугольный, то градусная мера одного из его углов равна

А) 100^о         В) 98^о        С) 91^о         D) 90^о         Е) 101^о


Что это такое? Да весьма просто - конечная цель обучения школьников. Не подумайте, что младших школьников, а выпускников средних школ, то есть 16-17 летних юношей и девушек.

Вот и делайте после этого сами вывод о том, куда катится уровень образования в Казахстане.

В заметке http://www.liveinternet.ru/users/kifar/post224214082/ (Область определения функции в Wolfram|Alpha) было подробно описано как находить область определения функции одной переменной на примерах решения тестовых заданий ЕНТ по математике на базе материалов 2012 года. Теперь настал черед рассмотреть вопрос об определении множества значений функции.

Как и в предыдущей статье мы обратимся к материалам тестов ЕНТ (аналог ЕГЭ в Казахстане) по математике 2010 - 2012 годов.

Для начала немного теории. Для отыскания множества значений функции Wolfram|Alpha использует запрос range, который имеет следующий формат:
 

range f(x)

где range так и переводится как множество значений или область значений; f(x) - конкретная функция, множество значений которой требуется вычислить.

Рассмотрим следующий пример по определению множества значений функции y = .

Как всегда для начала работы перейдем на главную страницу сервиса Wolfram|Alpha по адресу http://www.wolframalpha.com/ и введем запрос в виде range -x^2+8x-3 . На следующем рисунке указано как следует вводить наш запрос и получить на него ответ.

Для получения множества значений нашей функции в окне ввода запросов нажмем на заначек "=". Мы получим интересующий нас ответ

Кроме этого ответа среди результатов выполнения нашего запросы система Wolfram|Alpha изобразить множество значений нашей функции на числовой прямой, вычислит область определения нашей функции и построит график исследуемой функции в различных масштабах в декартовой системе координат.

Более полный вариант этой статьи с подробным разбором других примеров читайте здесь.

Как правило, на экзамене ЕНТ (аналог ЕГЭ в Казахстане) в каждом варианте содержится задание на вычисление области определения функции. Такие задания удобно решать при помощи сервиса Wolfram|Alpha.

Для вычисления области определения функции в Wolfram|Alpha есть правило (формат) запроса

domain f(x)
где domain буквально переводится как "область определения функции", а f(x) - это та функция, область определения которой вам необходимо вычислить. По такому формату запроса система Wolfram|Alpha выводит пользователю: область определения функции в терминах теории множеств, ее графическую иллюстрацию и схематическое изображение графика функции. Этого вполне достаточно, чтобы получить правильный ответ на соответствующее тестовое задание и сверить его с ответами для выбора.

Вот и вся небольшая теория по теме "область определения функции". А теперь перейдем к конкретной практике и рассмотрим несколько примеров на вычисление области определения функций при помощи системы Wolfram|Alpha. Отметим лишь, что все эти задания взяты мной из сборника для подготовки ЕГЭ по математике 2012 года без соответствующих пяти ответов для выбора правильного среди них.

1. Найдите область определения функции у = 1/(x² + x).

Сначала перейдем на главную страницу сервиса Wolfram|Alpha по адресу http://www.wolframalpha.com/ и введем запрос в виде domain 1/(x^2+x) . На следующем рисунке указано как следует вводить наш запрос и получить на него ответ.


После указания "получить ответ" (нажатия на кнопку "=") мы получить следующий искомый результат.


Понятно, что это простое задание можно было достаточно быстро решить устно, не прибегая к помощи Wolfram|Alpha. Его мы рассмотрели для того,чтобы объяснить технику работы по вычислению области определения и множества значений функции в системе Wolfram|Alpha.

Теперь рассмотрим решение более сложного задания.
2. Найдите область определения функции:.
"Переведем" это задание на язык понятный системе Wolfram|Alpha: domain 2+sqrt(sin(x/2)). Выполним процедуру получения ответа как и в предыдущем примере.

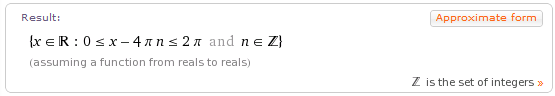
Этот ответ однозначно соответствует правильному ответу, который содержится в сборнике тестов, откуда был заимствован этот пример.
3. Найдите область определения функции: .

Как видно из рисунка система Wolfram|Alpha дала хотя и правильный,но не очень корректный ответ: х < -1 или 2х > 1. Это, как говорится издержки системы. Вообще, на Wolfram|Alpha надейся, но сам не плошай!

Вот пример, решение которого в системе Wolfram|Alpha никак не соответствует ответам из сборника тестов для подготовки к ЕНТ 2012 года.

4. Найдите область определения функции у =
Запись данной функции в системе Wolfram|Alpha имеет вид domain sqrt(sin(x)-sqrt(3)cos(x)). Полученное решение представлено на следующем рисунке.

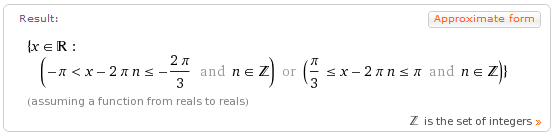
Это решение не совпадает ни с одним из ответов для выбора правильного из них в соответствующем тестовом задании. Поэтому следует помнить, что система Wolfram|Alpha иногда дает и сбои.

Задания для самостоятельного решения

1. Найдите область определения функции: у = .
2. Найдите область определения функции: у =
3. Найдите область определения функции:.
4. Найдите область определения функции: .
5. Найдите область определения функции: у = log₂(x + 6) + log₃(6 - x).
6. Найдите область определения функции: .

На сайте http://egeent.ucoz.ru я уже опубликовал несколько статей о применении системы Wolfram Alpha для подготовки к ЕНТ и ЕГЭ по математике. Уверен, что такие системы еще не нашили тех, кто их мог бы по достоинству оценить в качестве инструментов преподавания учебных дисциплин.

Теперь же я нашел плагины для встройки этой системы в практически любой браузер. Таким образом система Wolfram Alpha всегда у меня под рукой (в прямом и переносном смысле этого слова). Эти плагины можно найти по адресу http://www.wolframalpha.com/downloads.html?showall и буквально в один клик мыши установить на своем браузере. Коллекция плагинов и расширений Wolfram Alpha включает гаджет iGoogle и расширения для Firefox, Chrome, Safari, Internet Explorer и Opera.

После установки соответствующего плагина в правом верхнем углу браузера появляется кнопка соотвествующая логотипу системы Wolfram Alpha. После нажатия на нее появляется окно для ввода задания.

Теперь мне нетрудно посмотреть график любой функции типа cos(pi*x) / (-LN2*x), разложение многочлена 2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48 на множители, вычисление значения любого громоздкого арифметического выражения и т. п.

Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 11 - Окружность описанная около трапеции
Часть 12 - Центр окружности, описанной около четырехугольника
Часть 13 - Wolfram Alpha для браузера
Часть 14 - Задача из рассказа «Репетитор» Антона Павловича Чехова
Часть 15 - Рисунок-ключ к решению текстовой задачи
...
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения

В Казахстане некоторые деятели от образования стремятся внедрить в тесты ЕНТ так называемые логические задачи. Они считают, что эти задачи дадут возможность проверить логическое мышление будущих студентов.

Как всегда все начинается с благих намерений, а кончается ... . В этой статье рассмотрим решение одной из таких задач, а точнее одного из таких тестовых заданий с пятью ответами для выбора правильного среди них.

Вот это тестовое задание.

Завещание:

Если родится сын, ему достанется 2/3 всего состояния, жена получит 1/3 состояния;
Если родится дочь, ей достанется 1/3 всего состояния, жена получит 2/3 состояния;

Какую часть состояния получит жена,если родятся сын и дочь?

А) 3/4 B) 1/5 C) 2/7 D) 4/3 E) 4/7

Решение.

Среди ответов мне очень понравился ответ D). Согласно этого ответа жена получит 4/3 всего состояния, т. е. больше чем само состояние. Чудны дела твои господи ... !

Однако перейдем от шуток составителей этого задания к делу.

Из условия задания следует, что жена получает вдвое меньше чем сын и вдвое больше чем дочь. Значит, <доля сына>:<доля матери>:<доля дочери> = 4: 2 : 1. Поэтому в нашем случае жена получит 2 доли из 7, т. е. 2/7.

Ответ: 2/7.
Вот и вся задача на проверку логического мышления учащихся. Мне же эта задача напоминает задания из сборников логических упражнений "Решаем на досуге" типа "Математическая шкатулка", которые никакого отношения к школьному курсу математики не имеют.