Новый конкурс |
Математические маневры
Объединение пошаговой стратегии и олимпиады по математике
Эта игра начнётся завтра, 20.10 2010 в 20:10 мск в блоге "Математическая задача недели".
Имеется математический остров, вот он:
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
Карта его состоит из 11 областей. В каждой области есть несколько укреплений – задач. Игроки решают задачи и получают контроль над областью. Чтобы удержать область, нужно после захвата укрепить её своими задачами. Победит тот, кто захватит весь остров.
Как принять участие в маневрах?
Для этого в комментарии к заглавному посту блога сообшите свою форму участия: личную или командную, желаемый цвет (лучше в RGB-формате) и начинайте штурмовать укрепления. Если у вас нет территорий на острове, можете решать задачи в любой прибрежной области, если же есть, то в областях, смежных с контролируемыми.
Область переходит под контроль игрока, решившего последнюю нерешённую задачу в ней. Результаты игры будут обновляться примерно раз в сутки. В течение следующих после захвата суток игрок должен представить организаторам задачи (с решениями) для укрепления. В одной области можно разместить до 3 задач.
Задачи не должны включать термины, не изучающиеся в средней школе и на 1 курсе не физико-математических вузов. Тематика задач области не обязательно должна совпадать с тематикой задач, соответствующей её названию.
Баллы:
- Решение задачи первым: 5 баллов
- Решение задачи не первым (но в течение того же хода): 3 балла
- Захват области: 10 баллов
- За каждый ход удерживания области: 1 балл
|
Метки: математика олимпиада задача |
Завершена очередная интернет-олимпиада по математике |
Третья открытая интернет-олимпиада по математике
Решения и результаты
Завершилась третья открытая интернет-олимпиада по математике, которая проводилась совместно с ведущим Математического Марафона Владимиром Лецко.
- Решение задачи 1
- Решение задачи 2
- Решение задачи 3
- Решение задачи 4
- Решение задачи 5
- Решение задачи 6
- Решение задачи 7
- Решение задачи 8
- Решение задачи 9
- Решение задачи 10
Упорную борьбу за победу в туре с начала до конца вели Анатолий Казмерчук, Алексей Волошин иСергей Половинкин. В итоге Анатолий и Алексей разделили первое место, а вся троица далеко оторвалась от преследователей.
Виват лауреатам!
Итоговое положение участников
в XIII туре Математического марафона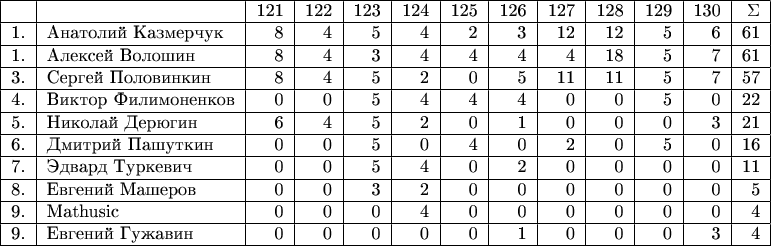
====================================
Итоги тематического конкурса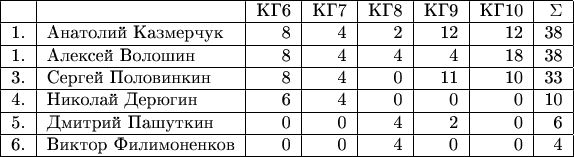
Скоро будут новые конкурсы, следите за новостями!
|
Метки: математика олимпиада решения |
Разбор задач первого дня тестирования (ЗНО) по математике |
Разбор задач первого дня тестирования (ЗНО) по математике
Закончился первый день ЗНО и можно приступить к обсуждению задач и ответов. Задавайте свои вопросы, постараемся ответить на все.
А пока – краткий разбор нескольких задач.
1. Выполнить действия
Здесь чтобы найти ответ достаточно уметь выполнять действия с дробями
2. Из точки А к окружности проведена касательная АВ (В – точка касания). Проведена и секущая АС, проходящая через центр О окружности. Найдите угол ВОС, если угол ВАС равен .

OB – радиус, проведённый к касательной, и угол АВО – прямой. В таком случае искомый угол ВОС является внешним углом треугольника АОВ и равен .
3. Решить неравенство 10>3x>4.
Разделив почленно на 3, получим:
4. Упростите
Те, кто разбирал примеры заданий ЗНО на свойства степеней, наверняка справились с этим заданием.
5. Решите уравнение
x=-3
6. С суммы наследства в пользу государства взимается налог в 0,5%. Сколько будет взято налога с суммы 32000 грн?
32000*0,005=160 (грн)
7. Длина окружности основания конуса равна см, высота равна 3 см. Найдите образующую конуса.

Т.к. длина окружности выражается по формуле , то радиус основания конуса равен 3 см. А т.к. радиус, высота и образующая формируют прямоугольный треугольник с катетами 3 и 4 , то образующая равна 5.
Учитывайте также, что завтра обязательно будут аналогичные задачи, готовьтесь и удачи!
|
Метки: математика решение задача тестирование 2010 зно |
Результаты второй открытой Интернет-олимпиады по математике |
Поздравляем победителей и участников олимпиады!
| I | Сергей Половинкин (e-science.ru) |
II | OpenGL (e-science.ru) |
III | Наталия Макарова |
txAlien (sciteclibrary.ru) |
Перовое и второе места раздилила задача 3 про нахождение закономерности и суммирование ряда.
Список участников в алфавитном порядке имён/ников:
| #sneg# (smekalka.pp.ru) |
| AlexAlkin (nazva.net) |
| Nogan (smekalka.pp.ru) |
| OpenGL (e-science.ru) |
| sweeper (civfanatics.ru) |
| txAlien (sciteclibrary.ru) |
| YURI (e-science.ru) |
| Илья (smekalka.pp.ru) |
| Наталия Макарова |
| Никифоров Стас |
| Николай (smekalka.pp.ru) |
| Сергей Половинкин (e-science.ru) |
Решения задач:
Спасибо всем участникам олимпиады! Желаем хорошо отдохнуть на каникулах!
|
Метки: математика 2010 олимпиада |
Решения задач третьего уровня пробного внешнего оценивания (ЗНО) по математике - 2010 |
Прошло очередное обновление раздела сайта по подготовке в внешнему тестированию (ЗНО) по математике. Теперь там можно ознакомиться с правильными решениями и ответами на следующие задачи пробного оценивания:
- Задачи 26-28: Формулы сокращённого умножения. Область значений функции. Стереометрия. Сечения.
- Задачи 29-31: Производная функции.
Текстовые задачи. Проценты.
Логарифм. - Задачи 32-34: Чётные и нечётные функции.
Уравнения: тригонометрические, рациональные, иррациональные.
Тема Планиметрия. - Задачи 35-36: Уравнения с параметрами. Модули.
Стереометрия.
А всего на сайте:
- 105 решений задач внешнего независимого оценивания;
- 112 решённых задач олимпиады Кенгуру;
- 85 задач, предлагавшихся на олимпиадах по математике;
- 23 статьи о занимательной математике;
- Работают тематические блоги, где регулярно появляются новые интересные материалы, занимательные задачи и ведётся общение с читателями.
Что ещё интересного:
Результаты олимпиады Кенгуру 2010, дипломы победителей и участников разосланы областным координаторам и отправляются в школы.
Приём решений задач второй открытой интернет-олимпиады по математике продлён до 18-00 пятницы, 21 мая.
На Десяти буквах началась неделя графиков. Можно узнать, по каким формулам построен вот такой цветик-семицветик и другие интересные кривые.
|
Метки: математика зно 2010 тестирование |
Задача о поиске радиоактивных шаров |
Задача
Имеется 15 шаров. Среди них 2 радиоактивных. Имеется счётчик Гейгера. Его можно поднести к группе шаров и узнать, есть ли в ней радиоактивные (но неизвестно - сколько их). За сколько замеров можно найти оба радиоактивных шара в группе из 15 шаров?
Задачи подобного рода, в которых нужно, пользуясь прибором с конечным числом состояний, выделить искомые предметы из многих или упорядочить предметы, регулярно появляются на математических форумах. Они традиционно вызывают серьёзные затруднения при решении и споры в ходе его обсуждения.
Однако если знать общий подход, решение их достаточно легко.
Общий метод решения таких задач состоит из четырёх шагов, которые мы и рассмотрим.
Другие новости
Идёт неделя самоописывающих выражений на Десяти буквах. Вы можете узнать, в каких математических выражениях число букв совпадает с их значением. К примеру, во фразе "два в кубе" букв ровно 8.
Проводится разбор задач олимпиады Кенгуру 2010. Также со дня на день мы вместе с читателями блога ожидаем её результатов.
Выкладываются решения задач пробного внешнего тестирования по математике. Начали рассматриваться задачи третьего уровня сложзности.
А на выходных вы успеете принять участие во второй открытой Интернет-олимпиады по математике
|
Метки: задача |
Решения задач пробного ЗНО |
Решения задач пробного ЗНО
В разделе сайта, посвящённом подготовке к независимому внешнему оцениванию по математике появились решения 25-ти задач, предлагавшихся на пробном тестировании.
- Задачи 1-4: Целые числа. Делимость.
Система координат. Окружность.
Дроби.
Графики. - Задачи 5-8: Прямоугольный параллелепипед.
Показательные уравнения.
Трапеция.
Рациональные и иррациональные числа. - Задачи 9-12: Арифметическая прогрессия.
Геометрия.
Статистика.
Степень с рациональным показателем. - Задачи 13-16: Векторы в пространстве.
Тригонометрия.
Стереометрия. Призма.
Рациональные неравенства. Дроби. - Задачи 17-19: Степень с рациональным показателем.
Теория вероятности.
Геометрия. - Задачи 20-22: Площадь криволинейной фигуры.
Стереометрия.
Логарифмические неравенства. - Задачи 23-25: Стереометрия.
Комбинаторика.
Геометрия.
Обсудить решения задач можно в блоге о подготовке к тестированию.
А тем временем:
Идёт вторая открытая Интернет-олимпиада по математике. Спешите приянть участие!
Появляются первые решения задач олимпиады Кенгуру 2010
В блоге о занимательной математике можно узнать, у какого числа количество цифр в факториале свопадает с самим числом, какой формулой описывается провисающая цепочка и ещё много чего интересного.
|
Метки: математика решение задача 2010 зно |
Решения примеров задач Независимого внешнего тестирования по математике 2010 года. |
Тема: Наибольшее и наименьшее значение функции.
Условие Найдите наименьшее значение функции y=x3-12x на отрезке [0;3]
Задание 33
Тема:Площадь криволинейной фигуры.
УсловиеНайдите площадь фигуры, ограниченной линиями y=x3, y=8, x=0
Задание 34
Тема: Задачи с параметрами, системы.
Условие Найдите наибольшее значение параметра а, при котором система
Задание 35
Тема: Логарифмические уравнения, модули.
Условие Решите уравнение |3lg x +1| – |lg x – 3| = 2. Если у уравнения один корень, запишите его в ответ, а если их больше – запишите СУММУ всех корней.
Задание 36
Тема: Стереометрия. Пирамида.
Условие Сторона основания правильной четырёхугольной пирамиды равна 6. Боковое ребро пирамиды наклонено к плоскости основания под углом 60o . Найдите площадь площадь S сферы, описанной вокруг пирамиды. В ответе запишите значение
Решения примеров задач внешнего тестирования 2010
Обсудить решения задач в блоге ЗНО 2010 по математике
Итак, публикация решений примеров задач внешнего оценивания закончена. С апреля в разделе подготовки к внешнему тестированию мы будем публиковать решения задач пробного ЗНО по математике.
|
Метки: математика задачи тестирование зно вно оценивание |
Решения примеров задач Независимого внешнего тестирования по математике 2010 года. Задания 29-31 |
Задание 29. Тригонометрия. Найдите значение выражения tga+ctga, если a=15o
Задание 30. Рациональные неравенства. Решите неравенство . В ответ запишите наименьшее целое число, удовлетворяющее этому неравенству. Если такого числа нет, то в ответ запишите число 100
Задание 31. Геометрия. В прямоугольнике ABCD: АB=6 см, ВС=8 см, K и L – середины сторон ВС и CD соответственно (см. рисунок). Найдите площадь треугольника AKL (в см2).
Решения примеров задач внешнего тестирования 2010
Обсудить задачи и задать вопросы можно в блоге ЗНО 2010
|
Метки: зно тестирование задача математика тригонометрия геометрия неравенство |
Процитировано 1 раз
Условия задач математической олимпиады Кенгуру: комбинаторика, последовательность, логика |
Задача 95. Выпускник, 3й уровень, 2009 год
Ордината вершины параболы y=x2+bx+c равна -7 Сколько целых чисел может находиться между корнями уравнения x2+bx+с=0?
А:6 или 7; Б: 4 или 5; В: 5 или 6; Г: только 5; Д: только 6;
Задача 96. Юниор, 3й уровень, 2008 год
Кенгуру прыгает только вперёд на 1 или на 3 метра. Он хочет преодолеть ровно 10 метров. Сколькими способами он может это сделать?
А: 28; Б: 34; В: 35; Г: 55; Д: 56;
Задача 97. Кадет, 3й уровень, 2007 год
Дана числовая последовательность такая, что a1=1, a2=2, a3=3, an+3= an+ an+1– an+2. Найдите a2007
А: -2006; Б: -2004; В: -2002; Г: 2008; Д: 2007;
Задача 98. Школьник, 3й уровень, 2007 год
Пять целых чисел написали по кругу так, что сумма никаких двух или трёх расположенных подряд не делится на 3. Сколько среди этих пяти чисел таких, которые делятся на 3?
А: 0; Б: 1; В: 2; Г: 3; Д: невозможно определить;
Задача 99. Малыш-3,4 классы, 3й уровень, 2008 год
Есть 5 коробок с карточками с буквами B, R, A, V, O.
В первой лежат B, V
Во второй лежат B, A, V, R
В третьей лежат A, B
В четвёртой лежит V
В пятой лежат B, R, A, V, O
Петя вытащил из коробок карточки так, чтобы в каждой коробке осталось по одной карточке и в разных коробках остались карточки с разными буквами. Какая буква останется во второй коробке?
А: B; Б: R; В: A; Г: V; Д: O;
Задача 100. Малыш-2 класс, 3й уровень, 2008 год
Маша подарила маме, бабушке, тёте и двум сёстрам по букету цветов. Цветы для сетсёр и тёти были одного цвета. Известно, что бабушке она подарила не розы. Какой из этих букетов получила мама?
А: Жёлтые тюльпаны; Б: Розовые розы; В: Красные гвоздики; Г: Жёлтые розы; Д: Жёлтые гвоздики;
Решения задач математической олимпиады Кенгуру и ответы
Вот мы и достигли отметки в 100 задач олимпиады Кенгуру. Правда, учитывая задачи мониторинга уровня знаний учащихся в 2009 году, на самом деле эта отметка была достигнута ранее, а всего сейчас на сайте:
- 112 решённых задач олимпиады Кенгуру;
- 61 решение задач внешнего независимого оценивания;
- 64 задачи, предлагавшихся на олимпиадах по математике;
- 22 статьи о занимательной математике;
- Работают тематические блоги, где регулярно появляются новые материалы, задачи и ведётся общение с читателями.
Самый новый открывшийся блог:
Десять букв, DesyatBukv.BlogSpot.com – блог про интересные числа, занимательные математические факты и удивительные конструкции. Каждый день можно узнать что-то новое. Блг назван так, потому что в самом словосочетнаии "десять букв", а также в транслитерированом, и в переведённом на английский, французский, болгарский, венгерский, испанский, каталанский, македонский, румынский, сербский и хорватский языки - действительно десять букв.
А в блоге Математические задачи недели открылись решения первого блока задач и стартовал
Математический аукцион!
Правила математического аукциона
Даётся исследовательская задача. Участники в комментариях предлагают свои варианты решения. Каждое решение, оказавшееся лучше присланного перед этим решения другого участника, оценивается всё большим количеством баллов. Если участник присылает несколько решений подряд, оценивается самое лучшее из них.
Задача
Число 210 делится на 21 и на 10.
Найдите как можно более длинное число, которое делится на все двузначные числа, образованные его соседними цифрами. (Нули внутри числа и одинаковые 2-значные фрагменты в нём не допускаются).
Ответы присылайте в комментарии в блог Математическая задача недели, чтобы удобнее было вести торги с участниками других форумов.
Участникам олимпиады Кенгуру 2010 желаем удачи на конкурсе!
|
Метки: кенгуру математика задача блог |
Условия задач математической олимпиады Кенгуру: тригонометрия, неравенства, геометрия |
Задача 89. Выпускник, 3й уровень, 2009 год
Найдите, при каких значениях острого угла a уравнение
(2cosa -1)x2 - 4x + 4cosa + 2 = 0
будет иметь два действительных положительных корня?
А:0o < a < 30o; Б: 0o < a < 60^0; В: 30o < a < 60^0; Г: 30o < a < 90^0; Д: 0o < a < 90o;
Задача 90. Юниор, 3й уровень, 2009 год
Последовательность целых чисел задаётся рекуррентно: a0=1, a2=2, an+2=an+(an+1)2. Чему равен остаток от деления a2009 на 7?
А: 0; Б: 1; В: 2; Г: 5; Д: 6;
Задача 91. Кадет, 3й уровень, 2008 год
Решением уравнения (x+22007)2 – (x–22007)2 = 22008 является:
А: 0,5; Б: 2; В: 22; Г: 22008; Д: 0;
Задача 92. Школьник, 3й уровень, 2009 год
Комплект домино состоит из 28 костяшек, которые образованы всеми возможными комбинациями количеств точек от 0 до 6 включительно. Сколько всего точек в наборе домино?
А: 84; Б: 105; В: 126; Г: 147; Д: 168;
Задача 93. Малыш-3,4 классы, 3й уровень, 2009 год
Сколько существует двузначных чисел, у которых цифра справа больше цифры слева?
А: 9; Б: 18; В: 26; Г: 30; Д: 36;
Задача 94. Малыш-2 класс, 3й уровень, 2009 год
Секретный агент хочет расшифровать код из шести цифр. Он знает, что сумма цифр на первом, третьем и пятом местах равна сумме цифр на втором, четвёртом и шестом местах. Какой из предложенных вариантов не может быть кодом?
А: 81**61;
Б: 7*727*;
В: 4*4141;
Г: 12*9*8;
Д: 181*2*;
Решения задач математической олимпиады Кенгуру и ответы
|
Метки: математика олимпиада кенгуру |
Условия задач математической олимпиады Кенгуру: тригонометрия, неравенства, геометрия |
Задача 83. Выпускник, 3й уровень, 2009 год
Каково максимальное значение выражения
sin a cos b + sin b cos c + sin c cos d + sin d cos a
для действительных a, b, c, d?
А:1; Б:2; В:3; Г:4; Д: 8;
Задача 84. Юниор, 3й уровень, 2008 год
Известно, что х и у - положительные действительные числа, и только одно из приведённых в ответах утверждений истинное. Какое?
А: x2 > 2y2; Б: x > 2y; В: x > y; Г: x2 > y2; Д: x > y2;
Задача 85. Кадет, 3й уровень, 2008 год
Некоторое количество прямых изобразили на бумаге так, что между ними есть углы величиной 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°. Найдите наименьшее количество прямых, для которых такое возможно.
А: 4; Б: 5; В: 6; Г: 7; Д: 8;
Задача 86. Школьник, 3й уровень, 2009 год
В стране Туфляндии у каждого жителя правая нога на один или на два размера больше левой. К сожалению, в магазине продаются пары обуви только одинакового размера. Чтобы сэкономить деньги, несколько друзей пошли в магазин и каждый из них купил одну пару обуви. Когда они обменялись обувью, один ботинок 36 размера и один ботинок 45 размера оказались лишними. Какое наименьшее количество человек могло быть в этой группе?
А: 5; Б: 6; В: 7; Г: 8; Д: 9;
Задача 87. Малыш-3,4 классы, 3й уровень, 2009 год
На клумбе расцвели цветы: белый, красный, синий и жёлтый. Пчела Майя подлетает к каждом цветку всего 1 раз. Сначала она летит к красному цветку, а затем – к остальным. Майя не может лететь с жёлтого цветка сразу на белый. Сколькими способами пчела Майя может посетить все 4 цветка?
А: 1; Б: 2; В: 3; Г: 4; Д: 6;
Задача 88. Малыш-2 класс, 3й уровень, 2008 год
Петя прибавляет 2, Назар отнимает 1, а Дима удваивает число. Каждый мальчик выполняет своё действие только один раз. В каком порядке им нужно выполнять эити действия, чтобы из 3 получить 9?
А: Дима, Петя, Назар;
Б: Петя, Дима, Назар;
В: Дима, Назар, Петя;
Г: Назар, Дима, Петя;
Д: Петя, Назар, Дима;
Решения задач математической олимпиады Кенгуру и ответы
|
Метки: математика олимпиада кенгуру задача тригонометрия неравенства геометрия |
Наши математические блоги |
Чтобы было удобнее общаться с читателями сайта Приглашение в мир математики и реагировать на ваши пожелания и вопросы, были созданы 3 тематических блога:
Математическая задача недели, Math-zn.BlogSpot.com – здесь раз в неделю появляется пакет олимпиадных задач. Решения можно присылать в скрываемые комментарии или по электронной почте. Вы сами можете участвовать в формировании пакетов задач, присылая интересные условия.
Задачи на эту неделю:
1) В треугольнике одна из медиан перпендикулярна одной из биссектрис. Найти стороны треугольника если они выражены тремя последовательными чётными числами.
2) Найти три последовательных натуральных числа, если известно что сумма цифр числа, образованного сложением кубов этих чисел, равна 27
3) Существует ли число, записанное только цифрами 3, которое делится на 93?
Задачи 1 и 2 прислал Семён Знаковян (*ALEX ALKIN*)
Математическая олимпиада Кенгуру 2010, Kenguru2010.BlogSpot.com – для обсуждения материалов раздела сайта, посвящённого олимпиаде Кенгуру. Также будут публиковаться фотоотчёты о проведении конкурса, результаты олимпиады, и, по прошествии установленного оргкомитетом срока, задачи 2010 года и их решения.
Независимое внешнее тестирование 2010, ZNO2010.BlogSpot.com – вопросы подготовки к ЗНО 2010. Пишите в комментарии сложные задачи школьного курса, и их решение будет объясняться.
|
Метки: математика задачи блоги |
Задачи математической олимпиады Кенгуру |
Условия задач математической олимпиады Кенгуру: целые числа, логика, геометрия
Задача 78. Студент, 3й уровень, 2001 год
Дядя Богдан наловил рыбы. Три самых больших рыбы он дал своей собаке, тем самым, уменьшив общий вес своего улова на 35%. Затем он дал три самых маленьких рыбы своему коту, уменьшив вес оставшейся рыбы на 5/13. Остальные рыбы семья съела на обед. Сколько рыб поймал дядя Богдан?
А:8; Б:9; В:10; Г:11; Д: 12;
Задача 79. Юниор, 3й уровень, 2000 год
В одной из подгрупп кубка чемпионов Европы участвовали 5 команд:, A, B, C, D, E. Пять спортивных изданий высказали свои прогнозы насчёт финалистов:
1)B, D;
2)C, E;
3)B, C;
4)A, B;
5)D, C.
Оказалось, что один из прогнозов был полностью верным, а в остальных указывалась лишь одна из команд-финалистов. Какие команды вышли в финал?
А: B, D; Б: C, E; В: B, C; Г: A, B; Д: D, C;
Задача 80. Кадет, 3й уровень, 1999 год
На плоскости даны 4 точки. Пять из шести расстояний между ними равны 7, 5, 5, 2 и 2. Тогда шестое расстояние может равняться:
А: 3; Б: 4; В: 7; Г: 10; Д: 12;
Задача 81. Школьник, 3й уровень, 2002 год
Чтобы очистить 4 своих аквариума, Ваня поселил в них улиток. Чтобы очистить один аквариум, нужны или 4 большие улитки, или 1 большая и 5 маленьких улиток, или 3 большие и 3 маленькие улитки. У Вани 15 больших улиток. Но в зоомагазине он может обменять одну большую улитку на 2 маленьких. Какое наименьшее количество больших улиток нужно обменять Ване, чтобы почистить все свои аквариумы?
А: 2; Б: 3; В: 4; Г: 5; Д: 6;
Задача 82. Малыш, 3й уровень, 2001 год
В футбольном матче победитель получает 3 очка, проигравший – 0, а ничья оценивается одним очком. После 31 матча моя любимая команда имела 64 очка, причём 7 матчей она сыграла вничью. Сколько раз проиграла моя любимая команда?
А: 0; Б: 5; В: 19; Г: 21; Д: 24;
|
Метки: олимпиада математика кенгуру |
Задачи математической олимпиады Кенгуру |
Условия задач математической олимпиады Кенгуру: системы счисления, геометрия, арифметика
Задача 73. Студент, 3й уровень, 2004 г.
Сколько положительных целых чисел могут быть записаны как a0+a13+a232+a333+a434, если a0, a1, a2, a3, a4 принадлежат множеству {-1, 0, 1}
А:5; Б:80; В:81; Г:121; Д: 243;
Задача 74. Юниор, 3й уровень, 2001 г.
Сколькими способами можно полностью покрыть прямоугольник со сторонами 2x8 костяшками домино 1x2 без наложений?
А:16; Б:21; В:30; Г:32; Д:34;
Задача 75. Кадет, 3й уровень, 2003 г.
По результатам контрольной работы, в классе средний балл мальчиков оказался равен 8,6, девочек – 9,8, а средний балл всех учеников в классе – 9,4. Какую часть класса составляют мальчики?
А: 1/4; Б: 1/3; В: 1/2; Г: 2/3; Д: невозможно определить;
Задача 76. Школьник, 3й уровень, 2003 г.
Сколько точек пересечения точно не могут иметь 4 прямые?
А: 1; Б: 2; В: 3; Г: 4; Д: 5;
Задача 77. Малыш, 3й уровень, 2001 г.
Маленький Мук и королевский скороход соревновались в беге на дорожке длиной 30 км, которая проходила вокруг большого луга. По условиям состязания, выиграет тот, кто обгонит другого, пробежав на один круг больше. Скороход пробегает круг за 10 минут, а Маленький Мук – за 6 минут. Оба стартуют одновременно из одного и того же места. Через сколько минут Маленький Мук победит?
А: 5; Б: 10; В: 15; Г: 20; Д: 25;
Решения и ответы на задачи математической олимпиады Кенгуру
P.S. Тем временем решения задач открытой интернет-олимпиады по математике продолжают поступать. Появление решений задач и списка победителей на сайте назначено на вторник, 2 марта, так что ещё не поздно приянть участие! :)
|
Метки: математика олимпиада задача кенгуру |
Задачи математической олимпиады Кенгуру |
Условия задач математической олимпиады Кенгуру: комбинаторика, делимость, геометрия
Задача 68. Студент, 3й уровень, 2006 год
Тест состоит из 10 вопросов, на каждый из которых нужно выбрать вариант ответа а) или б). Если на любые 5 вопросов ответить вариантом а), а на остальные пять – вариантом б), то обязательно как минимум 4 ответа окажутся верными. Сколько существуем вариантов расположения правильных ответов в тесте, которые обеспечивают такое его свойство?
А:2; Б:10; В:22; Г:252; Д: 5^5;
Задача 69. Юниор, 3й уровень, 2001 год
В коробке была 31 конфета. В первый день Кристина съела 3/4 от количества конфет, которые съел Петя в тот же день. На второй день Кристина съела 2/3 количества конфет, которые съел Петя в тот же день. После двух дней коробка осталась пустой. Сколько конфет из коробки съела Кристина?
А:9; Б:10; В:12; Г:13; Д:15;
Задача 70. Кадет, 3й уровень, 2005 год
Карл говорит правду в тот день, когда он не обманывает. Какое из следующих утверждений Карл не мог высказать в один день вместе с остальными?
А: Число моих друзей - простое;
Б: У меня столько же друзей среди мальчиков, сколько и среди девочек;
В: 288 делится на 12;
Г: Я всегда говорю правду;
Д: Три моих друга старше меня;
Задача 71. Школьник, 3й уровень, 1999 год
Какое наибольшее количество тупых углов могут образовать 6 лучей с общим началом?
А: 6; Б: 8; В: 9; Г: 12; Д: 15;
Задача 72. Малыш, 3й уровень, 2002 год
В каждом подъезде на каждом этаже 16-этажного дома есть по 4 квартиры. В каком подъезде и на каком этаже находится квартира №165?
А: 3 подъезд 9 этаж; Б: 3 подъезд 10 этаж; В: 3 подъезд 12 этаж; Г: 2 подъезд 13 этаж; Д: 3 подъезд 7 этаж;
Решения и ответы задач математической олимпиады Кенгуру
P.S. У вас ещё остаётся неделя, чтобы решить задачи открытой интернет-олимпиады по математике :)
|
Метки: математика олимпиада кенгуру задачи решения |
Результаты мониторинга уровня математических знаний учащихся: 7-9 классы |
Результаты мониторинга уровня математических знаний учащихся 7-9 классов на основе распределения ответов в математической олимпиаде Кенгуру-2009
Среди заданий математической олимпиады Кенгуру 2009 года, семь были выбраны для поведения мониторинга уровня знаний учащихся 7, 8 и 9 классов, выступавших в уровне «Кадет».
Условия задач:
Задача 8. Три точки Q, S и R лежат на одной прямой. Точка P расположена так, что угол QPS равен 12o и PQ=PS=RS. Найдите угол QPR.
А:24o; Б:42o; В:48o; Г:54o; Д: 96o;
Задача 10. На листе написаны числа 2, 6, 8, 10 и некоторое пятое число. Известно, что если все эти числа чётные, то среди них есть хотя бы один полный квадрат. Тогда пятое число не может равняться:
А:3; Б:4; В:9; Г:12; Д: 2009;
Задача 16. У скольких натуральных чисел количества цифр в десятичной записи их квадрата и куба совпадают?
А:0; Б:3; В:4; Г:9; Д: бесконечно много;
Задача 18. В стране рыцарей и лжецов 25 человек встали в очередь один за другим. Каждый, кроме первого из очереди сказал, что человек, стоящий сразу перед ним, врёт. Первый же сказал, что все, стоящие за ним – врут. Сколько лжецов в колонне? (Рыцари всегда говорят правду, а лжецы всегда врут)
А:0; Б:12; В:13; Г:24; Д: невозможно определить;
Задача 19. Дроби 1/5 и 1/3 отмечены на числовой оси. Где находится 1/4?
1/5__|__|__|__|__|__a__b__c__d__e__|__|__|__|__|__1/4
А:a; Б:b; В:c; Г:d; Д: e;
Задача 20. Велосипедист должен был прибыть в пункт назначения в 12:00. Если его скорость будет равняться 15 км/ч, то он прибудет в 11:00, а если его скорость будет равна 10 км/ч, то он прибудет в конечный пункт в 13:00. При какой скорости велосипедист прибудет в конечный пункт в назначенное время?
А:11 км/ч; Б:12 км/ч; В:12,5 км/ч; Г:13 км/ч; Д: 14 км/ч;
Задача 26. Во дворце между каждыми двумя залами и из каждого зала наружу есть не больше одной двери. Какое наименьшее возможное количество залов во дворце, если в нём всего 12 дверей?
А:4; Б:5; В:6; Г:7; Д: 8;
Решения задач и распределение ответов участников олимпиады Кенгуру-2009
P.S. Тем временем продолжается открытая интернет-олимпиада по математике: вы успеваете принять в ней участие.
|
Метки: математика кенгуру 2009 олимпиада |
Пакет задач математической олимпиады Кенгуру |
Пакет задач математической олимпиады Кенгуру: принцип Дирихле, цифры, множества
Задача 63. Студент, 3й уровень, 2000 г.
Экипаж космического корабля, приземлившегося на Марсе заметил интересные особенности марсиан:
- Все они или красные, или зелёные, или синие;
- Рост каждого – 1 метр;
- У марсианина от 2 до 5 голов;
- На теле у них от 3 до 20 антенн.
Какое минимальное количество жителей должно быть в марсианском посёлке, чтобы среди них заведомо можно было выбрать команду из 11 одинаковых игроков для футбольного матча с космонавтами? (Все 11 марсиан должны быть одного цвета, иметь одинаковое количество голов и одинаковое количество антенн)
А:216; Б:2161; В:2160001; Г:230051; Д: другое;
Задача 64. Юниор, 3й уровень, 2001 г.
Пусть а=19971998+19981999+19992000+20002001. Чему равна последняя цифра числа а?
А:0; Б:2; В:3; Г:4; Д:5;
Задача 65. Кадет, 3й уровень, 2004 г.
В июне во Львове число солнечных дней составило 25% о количества пасмурных, количество тёплых – 20% от количества холодных. Только три дня были солнечными и тёплыми. Сколько было пасмурных и холодных дней? (Всего в июне 30 дней)
А: 27; Б: 22; В: 19; Г: 17; Д: 7;
Задача 66. Школьник, 3й уровень, 2005 г.
У Полы и Билла вместе 18 гривен, у Билла и Джона – 12 гривен. У Джона и Марии – 10 гривен. Сколько гривен у Марии и Полы?
А: 16; Б: 20; В: 24; Г: 25; Д: 48;
Задача 67. Малыш, 3й уровень, 2002 г.
Рассмотрим число 12321232123212321…, состоящее из 2002 цифр. Тремя последними цифрами этого числа будут:
А: 123; Б: 232; В: 321; Г: 212; Д: 321;
Решения и ответы задач математической олимпиады Кенгуру
P.S. Пока до олимпиады Кенгуру остаётся время, приглашаем испытать себя в открытой интернет-олимпиаде по математике :)
|
Метки: математика олимпиада кенгуру |
Процитировано 11 раз
Понравилось: 1 пользователю
Первая открытая Интернет-олимпиада проекта "Приглашение в мир математики" |
Задание олимпиады состоит из семи задач, правильное решение каждой задачи оценивается в 7 баллов. Присылайте решения по адресу: intelmath@narod.ru
Подведение итогов олимпиады состоится 2 марта 2010 года.
1.Игра со спичками
В двух коробках лежат спички.
Два игрока делают ходы по очереди. За один ход можно:
а) забрать одну спичку из первой коробки, или
б) забрать по одной спичке из обеих коробок, или
в) забрать две спички из второй коробки, или
г) переложить одну спичку из второй коробки в первую.
Выигрывает тот, кто оставляет обе коробки пустыми.
Кто (игрок, начинающий игру, или его соперник) выиграет, если игроки не делают ошибок и вначале в первой коробке 20 спичек, а во второй десять?
2.Пять квадратов
Число 2010 представляется в виде суммы пяти последовательных квадратов:
2010=182+192+202+212+222
Наименьшее число, которое можно представить в виде суммы пяти последовательных натуральных квадратов – число 55:
55=12+22+32+42+52.
Как по виду числа определить, представляется ли оно в виде суммы пяти последовательных натуральных квадратов или нет?
3.Увеличение числа
Если в натуральном числе, не делящемся на 10, перенести предпоследнюю цифру на первое место, оно увеличится в n>1 раз. Для каждого натурального n, для которого такое возможно, приведите пример искомого числа.
4.Простая дробь
Согласно справочнику Гугла, 1 фунт равен 0,45359237 килограмма. Найдите простую дробь с минимальными числителем и знаменателем, значение которой отличается от этой десятичной дроби менее, чем на 2*10-5
5.Камень, Ножницы, Бумага
В игре «камень-ножницы-бумага» есть три фигуры. Камень считается сильнее Ножниц, Ножницы – сильнее Бумаги, а Бумага – сильнее Камня.
При игре вдвоём оба игрока одновременно выбрасывают на пальцах одну из фигур и, если они различны, определяется победитель. Если же выброшенные фигуры одинаковы – следует ещё одно выбрасывание, и так до выявления победителя.
При игре втроём игроки одновременно выбрасывают одну из фигур, и:
Если все три фигуры различны или все они одинаковы, следует перебрасывание;
Если один игрок выбросил более сильную фигуру, а два других – одинаковую, более слабую, то этот игрок объявляется победителем;
Если один игрок выбросил более слабую фигуру, а два других – одинаковую, более сильную, то далее следует определение победителя из этих двоих.
Сколько в среднем нужно провести выбрасываний, чтобы определить победителя среди троих игроков?
6.Что дальше?
Продолжите последовательность:
5, 7, 11, 13, 15, 19, 21, 29, 31, …
7.Самоописывающее равенство
Равенство 1+2=3 интересно тем, что первое его слагаемое равно общему количеству чётных цифр, использованных в равенстве, второе слагаемое равно общему количеству нечётных цифр в нём, а сумма равна общему количеству цифр в этом равенстве.
Составьте равенство
A+B+C+D+E+F+G+H+I+J=K, где
Слагаемое A равно общему количеству нулей в этом равенстве;
Слагаемое B равно общему количеству единиц в этом равенстве;
Слагаемое C равно общему количеству двоек
и т.д.
Слагаемое J равно общему количеству девяток, а
Сумма K равна общему количеству цифр в этом равенстве.
Удачи!!!
|
Метки: математика олимпиада 2010 |
Метод решения одного вида математических ребусов |
Утроение числа после перестановки цифр
Задача
Про некоторое число известно, что если переставить его последнюю цифру в начало, число увеличится втрое. Найдите наименьшее число с таким свойством.
Первая идея по решению: последняя цифра числа не должна быть меньше трёх (ведь затем она превратится в первую цифру утроенного числа). Допустим, она равна трём. Тогда число имеет вид х=*…*3, а утроенное число выглядит как3х=3*…*.
Но если первоначальное число оканчивается на тройку, то последняя цифра утроенного числа будет девяткой. 3х=3*…*9. Следовательно, первоначальное число оканчивается на 93: х=*…*93.
Умножив 93 на 3 и получив 279, узнаём две последние две цифры числа 3х=3*…*79. Теперь мы имеем три последние цифры числа х=*…*793. Это позволяет нам узнать последние три цифры утроенного числа: 3х=3*…*379, что, в свою очередь, да`т последние 4 цифры числа x=*…*3793.
Продолжать этот процесс мы должны будет до тех пор, пока между найденными кусками чисел x и 3x не установится требуемое соотношение. Однако когда количество вычисленных знаков перевалит за десяток-другой (к примеру: x = *…*82758620689655172413793 и 3x = 3*…*8275862068965517241379), начинаешь сомневаться. А есть ли вообще решение? Стоит ли продолжать? Вдруг в ход вычислений закралась ошибка? Может, последняя цифра была изначально взята неправильно? Существует ли более быстрый способ найти требуемое число или доказать, что его не существует?
И, действительно, более лёгкий способ решения этого математического ребуса есть!
|
Метки: математика ребус задача |






