Пакет задач олимпиады Кенгуру |
Пакет задач олимпиады Кенгуру №10: целые числа, уравнения, логика
Задача 48. Студент, 3й уровень, 1997 г.
Сколько целых решений имеет уравнение
x(x+1)+(x+1)(x+2)+…+(x+9)(x+10)=1000x+1997?
А:0; Б:1; В:2; Г:6; Д: бесконечно много;
Задача 49. Юниор, 3й уровень, 1998 г.
Число X состоит из цифр 1, 2, 3, а число Y – из цифр 4, 5, 6. Мы знаем, что число X+Y чётное и что вторая цифра числа X равна двум. Какова последняя цифра числа X*Y?
А: нельзя однозначно установить; Б:2; В:6; Г:5; Д:4;
Задача 50. Кадет, 3й уровень, 1999 г.
В тесте было 30 вопросов. Каждый правильный ответ увеличивает количество набранных баллов на 7, а каждая ошибка или отсутствие ответа уменьшает количество баллов на 12. Саша, выполнив тест, набрал 77 баллов. Сколько ошибок он сделал?
А: от 0 до 4; Б: от 5 до 8; В: от 9 до 12; Г: о 13 до 16; Д: невозможно определить;
Задача 51. Школьник, 3й уровень, 2000 г.
Имеются 3 коробки и 3 предмета: монета, игрушечная черепаха и горошина. У каждой коробке есть только один предмет, причём:
- Зелёная коробка находится левее голубой;
- Монета находится левее горошины;
- Красная коробка стоит правее черепахи;
- Горошина правее красной коробки;
В какой коробке монета?
А: в красной; Б: в зелёной; В: в голубой; Г: невозможно определить однозначно; Д: условия задачи противоречивы;
Задача 52. Малыш, 3й уровень, 2001 г.
В обувном магазине для животных на 10 полках было по 12 пар обуви. Первыми покупателями были пять многоножек. Первые три из них купили по 30 пар, а две следующие – по 5 пар каждая. Сколько пар обуви осталось в магазине после визита этих покупателей?
А:10; Б:15; В:20; Г:25; Д:30;
Решения задач олимпиады по математике Кенгуру
|
Метки: математика олимпиада кенгуру |
Решения примеров задач Независимого внешнего тестирования по математике 2010 года |
Задание 26. Многочлены. Формулы сокращённого умножения.
Установите соответствие между заданными выражениями (1-4) и выражениями, которые им тождественно равны (А-Д)
- (2a+b)2
- (2a-b)(b+2a)
- (a-2b)2
- (a+2b)(2a-b)
А. 4a2-b2
Б. 4b2-2ab+a2
В. 2a2+3aY-2b2
Г. 4a2+4ab+b2
Д. 4b2-4ab+a2
Решение
Знание формул сокращённого умножения значительно ускорит решение этого задания.
Выражение 1 раскладывается по формуле квадрата суммы: (2a+b)2=4a2+4ab+b2.
Выражение 2 – это произведение разности и суммы двух чисел и является разностью их квадратов: (2a-b)(b+2a)=4a2-b2
Выражение 3 раскладывается как квадрат разности: (a-2b)2=4b2-4ab+a2. (Обратите внимание, что составители заданий специально решили нас запутать и написали слагаемые в правильном варианте в обратном порядке).
Выражение 4 – единственное из вариантов, которое нужно просто перемножить и привести подобные: (a+2b)(2a-b)=2a2+3aY-2b2 (Кстати, здесь правильный ответ можно получить и без полного перемножения. Достаточно определить, что коэффициент при a2 равен двум.)
Ответ: 1-Г, 2-А, 3-Д, 4-В
Задание 27. Преобразования графиков функций.
Установите соответствие между заданными геометрическими преобразованиями графика функции y=cosx (1-4) и функциями, полученными в результате преобразований (А-Д)
- График функции y=cosx параллельно перенесли вдоль оси Ox на две единицы влево
- График функции y=cosx параллельно перенесли вдоль оси Oy на две единицы вниз
- График функции y=cosx сжали к оси Ox в два раза
- График функции y=cosx сжали к оси Oy в два раза
А. y=cos(2x)
Б. y=0,5cosx
В. y=cos(x-2)
Г. y=cos(x+2)
Д. y=cosx-2
|
Метки: математика тест 2010 зно |
Подготовка к экзамену GRE по математике |
Подготовка к экзамену GRE по математике
Представляем наш новый проект: блог MathGRE.Blogspot.com для готовящихся к экзамену GRE по математике. Экзамен GRE (Graduate Record Examinations) является обязательным условием для поступления в аспирантуру в США. В блоге каждый день появляются математические и логические задачи различного уровня сложности, предлагаемые на экзамене.
Экзамен GRE и олимпиада по математике "Кенгуру" имеют много общего. Задачи представляют собой тестовые задания и их требуется решать быстро. В тест входят задания различного уровня сложности (хотя сложность не указывается прямо).
Хотя задания в целом, как правило, несложные, ограничения по времени заставляет искать для них кототкие (и поэтому красивые) решения. Отдельный интерес представляет решение логических задач, к примеру, на составление расписания, удовлетворяющего некоторым условиям.
Поскольку все задания и решения публикуются на английском языке, блог будет полезен и для желающих расширить свой словарный запас.
Обзоры математических ресурсов на сайте Приглашение в мир математики:
- Образовательный видеопортал UniverTV.ru: здесь можно посмотреть видеозаписи лекций, образовательные фильмы и анимационные ролики.
- Умные видео на SmartVideos.Ru: Общенаучный ресурс с интересными и познавательными видеороликами
- Математические библиотеки в Сети: Web-обзор интернет библиотек математической литературы. Вы узнаете, откуда можно скачать книги Гарднера, Перельмана, журналы Квант и "Библиотеку математического кружка". Приводятся ссылки на источники литературы как по элементарной, так и по высшей математике.
- Онлайн энциклопедия целочисленных последовательностей: Web-обзор полезного математического ресурса, предоставляющего неоценимую помощь в математических исследованиях. Описываюся правила работы с энциклопедией, приводятся несколько занимательных задач с решениями.
|
Метки: математика gre экзамен |
Приглашение в мир математики |
Как вспомнить забытую тригонометрическую формулу? Вывести!
На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.
А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.
Будем опираться на следующие формулы:
- Основное тригонометрическое тождество: sin2a+cos2a = 1
- Определение тангенса:
- Определение котангенса:
- Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
- Формула косинуса суммы: cos(a+b) = cosacosb-sinasinb
Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:
- Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb-cosasinb
- Косинус разности: cos(a-b) = cosacos(-b)-sinasin(-b) = cosacosb+sinasinb
Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:
- Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
- Косинус двойного угла: cos2a = cos(a+a) = cosacosa-sinasina = cos2a-sin2a
Аналогично получаются и формулы других кратных углов:
- Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a-sin2a)sina = 2sinacos2a+sinacos2a-sin3a = 3sinacos2a-sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
- Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa-sin2asina = (cos2a-sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa
Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол - острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sina = 3,а cosa = 4.
(Из математического юмора)
Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывод возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:
- Связь тангенса и косинуса:
Так что решением этой задачи будет:
(Т.к. угол острый, при извлечении корня берётся знак +)
- Аналогично получаем связь котангенса и синуса:
Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:
- Формула тангенса суммы:
. Разделив числитель и знаменатель на произведение косинусов, получим:
Сразу выводится и
- Формула тангенса двойного угла:
И формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:
cos2a = cos2a-sin2a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos2a-sin2a+cos2a+sin2a
2cos2a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:
- Косинус половинного угла:
Знак берётся в зависимости от квадранта.
Аналогично, отняв от левой части равенства единицу, а от правой - сумму квадратов синуса и косинуса, получим:
cos2a-1 = cos2a-sin2a-cos2a-sin2a
2sin2a = 1-cos2a
- Cинус половинного угла:
И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, by. Тогда
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.
Поскольку a = x+y, by, то . Поэтому
- Представление суммы синусов в виде произведения:
Сразу же можно вывести
- Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5sin(a+b)+sin(a-b)
Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.
|
Метки: математика формула тригонометрия |
Информация о проведении математической олимпиады "Кенгуру без границ" в 2010 году |
Уважаемые читатели! Поздравляем Вас с Новым годом и желаем здоровья и творческих успехов и благополучия!
Уже скоро состоится олимпиада Кенгуру 2010. Чтобы показать на ней высокие результаты, рекомендуем прочитать советы по подготовке к олимпиаде по математике, ознакомиться с наиболее типичными ошибками, выявленными в ходе мониторинга в 2009 году, а также разобрать решения задач олимпиады Кенгуру прошлых лет.
Целью конкурса является популяризация математических идей и поддержка талантливых школьников, развитие их интеллектуальных способностей, активизация творческой деятельности учителей, выработка методических рекомендаций по совершенствованию учебных программ и учебников путем анализа статистических данных результатов конкурса.
1. Оргкомитет конкурса
Организация и проведение в Украине Международного математического конкурса "Кенгуру" возлагается на Центральный организационный комитет, который действует на базе Львовского физико-математического лицея при Львовском национальном университете имени Ивана Франко (директор лицея - Марьян Добосевич).
Адрес центрального оргкомитета:
ул. Караджича, 29, г. Львов,
79054
тел.-факс: (032) 2401700,
e-mail: kangaroo@lpml.com.ua.;
www.kangaroo.com.ua.
К полномочиям Центрального оргкомитета относится:
- решение вопросов по проведению конкурса, обработки бланков ответов участников, награждения победителей, обнародование результатов;
- информирование Международной ассоциации "Кенгуру без границ" и педагогов Украины о результатах конкурса;
- формирование пакета предложений в Международную Ассоциацию "Кенгуру без границ" для проведения конкурса "Кенгуру" в будущем году;
- делегирование части своих полномочий региональным координационным центрам при подписании соответствующего двустороннего соглашения;
- выработка методических рекомендаций по совершенствованию учебных программ и учебников, подготовка учебно-методических пособий.
2. Участие в конкурсе
В конкурсе могут принимать участие все желающие учащиеся 2 - 11 классов общеобразовательных учебных заведений всех форм собственности.
Конкурс в общеобразовательных учебных заведениях проводят координаторы конкурса или учителя этой школы.
Для участия в конкурсе ученик должен зарегистрироваться у координатора конкурса в своей школе или у регионального координатора в другом образовательном учреждении, где будет проводиться конкурс.
Координатор заполняет заявку на участие в конкурсе и направляет ее в адрес Центрального оргкомитета вместе с копией перевода благотворительного пожертвования не позднее 14 февраля 2010 года
Конкурс проводится в шести возрастных группах:
МАЛЫШ 2 - для учеников 2 классов;
МАЛЫШ 3-4 - для учеников 3 - 4 классов;
ШКОЛЬНИК - для учеников 5 - 6 классов;
КАДЕТ - для учеников 7 - 8 классов;
ЮНИОР - для учеников 9 - 10 классов;
ВЫПУСКНИК - для учеников 11 классов.
Рекомендуемый размер благотворительного взноса составляет 10 гривен от каждого участника и полностью используется для покрытия расходов на организацию и проведение конкурса. До 10% собранных пожертвований могут предназначаться для обеспечения организации и проведения конкурса в учебном заведении или объединении учебных заведений.
Примечание: В целях исполнения приказа Министерства образования и науки Украины от 24.05.2000 № 149 и согласно этим ПРАВИЛАМ всем заинтересованным в проведении конкурса лицам необходимо перечислять благотворительные пожертвования через отделения Сберегательного банка и других банков на расчетный счет благотворительного фонда "Лицей".
Львовское отделение Укрэксимбанка
Р / с 260010060560 МФО 325718
код 22360064 (с пометкой "Благотворительные пожертвования")
Получатель - Благотворительный фонд "Лицей"
3. Порядок проведения конкурса
Конкурс проводится в один день: четверг, 18 марта 2010, во всех регионах Украины по одинаковым задачам для каждой возрастной группы.
Местные ячейки проведения конкурса получают задания за несколько дней до его начала.
Конверты с заданиями открываются в день проведения конкурса в присутствии участников.
Количество листов с заданиями и бланков ответов высылается соответственно заявке об участии и копии перевода благотворительного взноса.
Перед началом конкурса координатором проводится детальный инструктаж участников о правилах проведения конкурса и заполнении бланка ответов.
Все учителя, которые проводят конкурс в данном учебном заведении, подписывают прилагаемый документ, в котором обязуются провести конкурс согласно данным правилам. В случае отсутствия такого документа работы учащихся данного учебного заведения могут быть изъяты из проверки.
Главное требование к координаторам и участникам конкурса - самостоятельная и честная работа над задачами.
Участники конкурса сидят за партами по одному.
Пользоваться калькулятором, учебниками и математическими таблицами категорически запрещается, расчеты и вычисления проводятся только на чистом листе бумаги. (Возьми на вооружение наши советы о том, как вспомнить забытую формулу).
Каждый участник конкурса получает листок с заданием, который затем оставляет себе, и бланк ответов участника, который после окончания конкурса отдает координатору.
Конкурс длится 75 минут - время на решение задач без учета продолжительности инструктажа.
После окончания работы над заданиями координатор собирает все бланки ответов вместе с регистрационными бланками для учеников и учителей, запаковывает в конверт, скрепляет печатью школы в присутствии нескольких наблюдателей (участников конкурса) и высылает в адрес Центрального оргкомитета с пометкой "Кенгуру".
Каждый участник и координатор конкурса может выразить в письменной форме свои замечания по проведению конкурса.
Все претензии относительно переданных результатов оргкомитетом принимаются до 1 июля 2009 года.
Бланки ответов участников конкурса сохраняются до 1 сентября 2009 года в Центральном оргкомитете, после чего утилизируются.
По любым вопросам проведения конкурса можно обращаться в адрес Центрального организационного комитета по проведению конкурса в Украине.
4. Содержание и структура задач
Задание для участников нынешнего конкурса предложено и утверждено Международным форумом ассоциации "Кенгуру без границ" в Берлине.
Для учеников 2 классов предлагается 15 интересных тестовых заданий различной степени сложности: 5 - трёхбалльных, 5 – четырёхбалльных, 5 - пятибалльных. Для учеников 3 - 4 классов предлагается 24 тестовых задания разной степени сложности: 8 - трёхбалльных, 8 - четырёхбалльных, 8 - пятибалльных, а для других участников конкурса - 30 заданий, из них 10 - трёхбалльных, 10 - четырёхбалльных, 10 - пятибалльных.
К каждому заданию предлагается пять вариантов ответа, среди которых есть лишь один правильный.
5. Оценивание результатов
На специальном бланке ответов необходимо указать только один правильный ответ.
Если выбраны два и более ответа на одну задачу, то ответ считается неправильным.
Неправильный ответ или его отсутствие оценивается в 0 баллов.
Максимальное количество баллов, которое может получить участник: для учеников 2 классов - 60 баллов; для учеников 3 - 4 классов - 96, для учащихся 5 - 11 классов - 120 баллов.
Основным критерием оценивания результата является суммарное количество баллов, набранное одним участником.
6. Поощрение участников конкурса
Поощрение участников конкурса осуществляется за счет благотворительных взносов участников и привлеченных спонсорских средств на местах.
Каждому участнику вручается специальный сертификат участника Международного математического конкурса "Кенгуру", который при необходимости может быть заверен дирекцией учебного заведения, проводившего конкурс, и информационный вестник.
Победители из наиболее активных школ-участниц будут приглашены в летние математические лагеря, и 15 из них будут представлять Украину в международных математических лагерях в Польше, Румынии и Литве. (Дополнительный стимул к активному участию в конкурсе могут дать фотоотчёты сборов участников и координаторов олимпиады Кенгуру)
7. Подведение итогов конкурса
Результаты конкурса, полученные путем обработки бланков ответов участников, публикуются не позднее, чем через восемь недель после его проведения.
Результаты вместе с сертификатами и информационными вестниками рассылаются во все местные ячейки проведения конкурса.
Центральный оргкомитет на основе полученной при проверке базы данных делает статистический анализ результатов, обрабатывает все замечания относительно проведения конкурса и его задач.
Аналитический отчет о результатах проведения конкурса направляется в управления образования и науки областных (городских) государственных администраций, институтов последипломного педагогического образования.
|
Метки: математика олимпиада кенгуру 2010 |
Решения примеров задач внешнего независимого тестирования 2010 |
Раздел, посвящённый подготовке к внешнему независимому тестированию 2010 года пополинился решениями примеров задач внешнего независимого тестирования 2010. Сейчас доступны решения 25 задач с выбором правильного ответа. Следите за обновлениями, этот список будет регулярно пополняться.
- Задания 1-4: Проценты. Векторы. Геометрическая прогрессия. Круг и окружность.
- Задания 5-8: Свойства неравенств. Действия с рациональными числами. Степень с рациональным показателем. Стереометрия. Пирамида.
- Задания 9-12: Математическая статистика. Степень с рациональным показателем. Стереометрия. Куб. Свойства логарифма.
- Задания 13-16: Показательные неравенства. Стереометрия. Объёмы. Конус. Функция. Периодичность. Вписанные углы.
- Задания 17-19: Теория вероятности. Признаки делимости. Тригонометрические уравнения.
- Задания 20-22: Стереометрия. Декартовы координаты в пространстве. Планиметрия. Параллелограмм. Свойства производной.
- Задания 23-25: Комбинаторика. Теорема косинусов. Стереометрия. Объёмы тел.
|
Метки: решение задача тестирование 2010 вно зно |
Процитировано 1 раз
Свойства числа 2010 |
Скоро новый, 2010 год. Это значит, что с большой степенью вероятности, число 2010 будет фигурировать в условиях задач олимпиад по математике. Рассмотрим некоторые свойства этого числа и интересные факты, связанные с ним.
- Число 2010 раскладывается на простые множители следующим образом. 2010=2*3*5*67
- Всего у числа 2010 16 делителей. Это числа 1, 2, 3, 5, 6, 10, 15, 30, 67, 134, 201, 335, 402, 670, 1005 и 2010
- Число 2010 представляется в виде суммы двух простых чисел 84-мя способами. Например, 2010=7+2003=11+1999=13+1997=…=991+1019
- Представимо оно и в виде разности простых чисел, например: 2010=2017-7=2027-17=2029-19 и т.д.
- Ни в виде суммы, ни в виде разности двух квадратов число 2010 не представляется.
- Нельзя его получить и в виде суммы или разности двух кубов.
- Сумма всех натуральных чисел от 1 до 2010 равна 2021055. Её можно вычислить, умножив 2010 на следующее за ним число, 2011, и разделив произведение на 2.
- Если перемножить все натуральные числа от 1 до 2010, полученное произведение будет содержать 5769 цифр. Заканчивается факториал числа 2010 на 501 ноль.
- Луна удаляется от Земли со скоростью примерно 4 см в год. За 2010 лет расстояние до неё выросло на 80 метров 40 сантиметров.
- Если бы 2010 лет назад положили в банк сумму, эквивалентную 1 доллару всего под 1% годовых, сейчас на счету было бы 480 миллионов 440 тысяч 852 доллара 96 центов.
- Древние римляне записывали число 2010 так: ММХ
- Если начать с числа 2010 сиракузскую последовательность, будем получать числа 1005, 3016, 1508 и т.д. и придём к единице за 68 шагов.
- А в виде суммы трёх квадратов число 2010...
|
Метки: математика 2010 число |
Задача почти без данных |
Два мудрых визиря
С олимпиадными задачами на движение, в которых почти ничего не дано, мы уже имели дело. В следующей задаче на терию чисел данные тоже придётся добывать по крупицам - но тем больше удовольствия принесёт результат!
Условие
У одного султана было два мудрых визиря. Захотел он проверить, насколько они сообразительны. Позвал он их обоих и сказал:
- Я загадал два числа от 2 до 100. Вы должны их мне назвать.
При этом султан сообщил первому визирю произведение этих чисел, а второму - их сумму.
Первый визирь подумал и говорит:
- Я не знаю что это за числа
На что второй ответил:
- Я был в этом уверен.
Тогда первый говорит:
- В таком случае, я знаю, что это за числа.
Второй:
- Тогда и я знаю, что это за числа.
Какие числа загадал султан? Определи их, читатель, и ты окажешься мудрее обоих мудрецов, ибо они узнали числа, зная их сумму или произведение, а ты же не знаешь об этих числах ничего!
Это ещё одна из задач математического фольклора, способных спровоцировать форумную войну, будучи загаданной в интернете. Поэтому постараемся разобрать её решение довольно подробно.
|
Метки: математика теория чисел задача |
Пакет задач олимпиады Кенгуру 2009 года: комбинаторика, проценты, ребус |
Из-за карантина у учеников Украины появилось лишних 3 недели на подготовку к математической олимпиаде. Советуем использовать это время с толком и потренироваться на задачах олимпиады Кенгуру 2009 года.
Задача 42. Выпускник, 3й уровень, 2009
Сколько существует 10-значных чисел, состоящих только из цифр 1, 2 и 3 таких, в которых соседние цифры отличаются на 1?
А: 16; Б: 32; В: 64; Г: 80; Д:100;
Задача 43. Юниор, 3й уровень, 2009
На выборах мера города Кенгуруполя было зарегистрировано 2 кандидата. После обработки n% бюллетеней для голосования избирательная комиссия сообщила жителям, что кандидат А набрал 62% голосов, а кандидат В – 38% голосов. При каком минимальном целом n эти предварительные результаты выборов гарантируют победу кандидату А, если недействительных бюллетеней не будет? Мер избирается простым большинством.
А: 55;Б:62; В: 81; Г: 87; Д: 93;
Задача 44. Кадет, 3й уровень, 2009
В уравнении K+A+N+G+A+R+O+O=56 разные быквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры. Тогда значение суммы A+O равняется:
А: 18;Б:17; В: 16; Г: 15; Д: однозначно определить невозможно;
Задача 45 . Школьник, 3й уровень, 2009
Дано 4 утверждения о натуральном числе А:
А делится на 5, А делится на 11, А делится на 55, А меньше 10. Известно, что два из них правильные, а другие два – неправильные. Тогда А равняется:
А: 0;Б:5; В: 10; Г: 11; Д: 55;
Задача 46. Малыш – 3,4, 3й уровень, 2009
Маша коллекционирует фотографии известных спортсменов. Количество фотографий, которые она собирает за каждый год равно количеству фото, собранных за два предыдущих года. В 2008 году она собрала 60 фотографий, а в этом – 69. Сколько фотографий собрала Маша в 2006 году?
А: 20;Б: 24; В: 36; Г: 40; Д: 48;
Задача 47. Малыш – 2, 3й уровень, 2009
Серёжа подбрасывал игральный кубик четыре раза и каждый раз записывал полученное число очков. Сложив эти числа, он получил 21 очко. Какое наибольшее количество раз могла выпадать тройка?
А: 0;Б: 1; В: 2; Г: 3; Д: 4;
Решения задач олимпиады Кенгуру 2009
|
Метки: кенгуру математика 2009 |
Чего ожидать на внешнем независимом тестировании по математике 2010 года. |
Фоматы и тематика заданий тестирования
В независимом тестировании 2010 года будет 36 заданий трёх уровней. Это в полном смысле слова тестирование, поскольку задания, требующие развёрнутого решения будут полностью исключены.
Из этих 36 заданий:
- 25 требуют выбора одного правильного варианта ответа из 5 предложенных и оцениваются 1 баллом.
- 3 задания нового формата требуют установления взаимосвязей. Скажем, есть два столбика с выражениями и необходимо для выражения в левом столбце найти тождественное ему выражение в правом. Всего в каждом задании требуется установить 4 взаимосвязи, так что максимум баллов за каждое задание – 4.
- 8 заданий, требующих найти ответ самостоятельно и вписать его в соответствующее поле бланка. Правильный ответ на такие задания оценивается в 2 балла.
Итого максимальное количество баллов, которое можно набрать, правильно решив все задания внешнего тестирования равно 53.
Распределение тем заданий представлено в таблице:
Предмет | Темы | Виды заданий | Всего | ||
На выбор правильного ответа | На определение соответствий | На самостоятельный поиск ответа | |||
Алгебра | Числа и выражения | 6 | 1 | 1 | 8 |
Уравнения и неравенства | 3 | 0 | 3 | 6 | |
Функции | 3 | 1 | 2 | 6 | |
Элементы комбинаторики, начала теории вероятности и математической статистики | 3 | 0 | 0 | 3 | |
Геометрия | Планиметрия | 5 | 0 | 1 | 6 |
Стереометрия | 5 | 1 | 1 | 7 | |
Всего | 25 | 3 | 8 | 36 | |
По сложности задания делятся следующим образом:
Предмет | Темы | Сложность заданий | Всего | ||
Простые | Средние | Сложные | |||
Алгебра | Числа и выражения | 2 | 6 | 0 | 8 |
Уравнения и неравенства | 1 | 2 | 3 | 6 | |
Функции | 1 | 3 | 2 | 6 | |
Элементы комбинаторики, начала теории вероятности и математической статистики | 0 | 3 | 0 | 3 | |
Геометрия | Планиметрия | 2 | 3 | 1 | 6 |
Стереометрия | 1 | 5 | 1 | 7 | |
Всего | 7 | 22 | 7 | 36 | |
На выполнение всех заданий тестирования отводится 150 минут.
Материалы для подготовки к внешнему независимому тестированию по математике
|
Метки: математика подготовка тестирование 2010 зно |
Процитировано 1 раз
Подготовка к внешнему независимому оцениванию по математике 2010 года |
В программе Независимого внешнего оценивания 2010 года математика является обязательным предметом для поступления в технические, технологические, экономические, и, разумеется, в естественные и математические вузы. Поэтому тем, кто серьёзно настроен на получение после школы престижной и востребованной специальности, готовиться стоит начинать уже сейчас.
Стоит начать с разбора решений заданий внешнего независимого оценивания 2009 года:
- Задания 1-5: Преобразование рациональных выражений. Свойства углов треугольника. Свойства степеней с рациональным показателем. Арифметическая прогрессия. Делимость.
- Задания 6-10: Показательные неравенства. Подобие треугольников, теорема Фалеса. Проценты. Преобразование рациональных выражений. Сравнение дробей.
- Задания 11-15: Свойства функций: чётность/нечётность. Векторы. Теория вероятности. Производные. Стереометрия.
- Задания 16-20: Преобразования графиков функций. Тригонометрические уравнения. Комбинаторика. Теорема косинусов. Подобие тел.
- Задания 21-25: Степени с рациональным показателем. Планиметрия: средняя линия треугольника, теорема Пифагора. Тригонометрия, основное тригонометрическое тождество. Объёмы тел. Логарифмические уравнения.
- Задания 26-30: Решение задачи по вопросам. Рациональные неравенства. Стереометрия: площадь поверхности тел. Системы показательных уравнений. Исследование функций.
- Задания 31-33: Стереометрия: сечения. Площадь криволинейной трапеции. Иррациональные неравенства.
Задания 1-20 проходят в формате тестов, хорошо знакомому участникам олимпиады Кенгуру и требуют выбора одного ответа из пяти. Задания 21-30 требуют самостоятельного нахождения ответа участником. Задания 31-33 требуют также развёрнутого решения.
Для учителей математики при организации процесса подготовки будут интересны методические разработки.
Будьте в курсе дат регистрации, тренировки и тестирования.
Рекомендуем пройти также онлайн тест.
|
Метки: зно математика 2010 тестирование подготовка |
Процитировано 1 раз
Результаты мониторинга уровня математических знаний учащихся: 5-6 классы |
В задания олимпиады Кенгуру каждый год включается несколько задач, которые позволяют сравнить уровень математических знаний у учащихся разных классов. С результатами мониторинга 2009 года на семинаре координаторов в г.Яремче ознакомил представитель оргкомитета олимпиады, Роман Евгениевич Кокорузь.
Для мониторинга были выбраны четыре задачи:
Условие 12:
Стороны четырёхугольника ABCD равняются: AB=11, BC=7, CD=9, AD=3, а углы A и C – прямые. Чему равна площадь четырёхугольника?
Варианты ответа:
А:30; Б:44; В:48; Г:52; Д:60;
Условие 17:
Коробку размером 30х30х50 нужно наполнить одинаковыми кубиками. Какое минимальное количество кубиков позволит это сделать?
Варианты ответа:
А:15; Б:30; В:45; Г:75; Д:150;
Условие 19:
Восемь карточек, занумерованных числами от 1 до 8, положили в коробки А и В так, что суммы чисел в коробках равны. Если известно, что в коробке А всего 3 карточки, то можно быть уверенным, что:
А: три карточки в коробке В с нечётными номерами;
Б: 4 карточки в В имеют чётные номера;
В: карточка с номером 1 не в коробке В;
Г: карточка с номером 2 в коробке В;
Д: число 5 в коробке В;
Условие 23:
Комнаты отеля пронумерованы тремя цифрами. Первая цифра обозначает этаж, а следующие две – номер комнаты. Например, 125 означает 25ю комнату на первом этаже. В отеле 5 этажей, они пронумерованы от 1 до 5, с 35 комнатами, пронумерованными от 101 до 135 на первом этаже и аналогичным образом – на остальных. Сколько раз при нумерации комнат использовали цифру 2?
Варианты ответа:
А:60; Б:65; В:95; Г:100; Д:105;
Узнать, какие ответы преобладали над правильными решениями этих задач можно на нашем сайте
Советуем дать эти четыре задачи в своём классе и сравнить результаты со средними по стране.
|
Метки: математика кенгуру олимпиада мониторинг |
Обновление раздела сайта о математической олимпиаде Кенгуру |
Представлена статистика участия стран мира в олимпиаде.
В фотоальбом олимпиады добавлен фотоотчёт со Всеукраинского семинара координаторов в г.Яремче.
|
Метки: олимпиада математика статистика фото |
Математическая игра «Рыцарский турнир» |
Две шашки-рыцари стоят на противоположных краях прямоугольной доски 2х33 доски. Между ними 31 клетка. Начальная скорость каждого рыцаря – единица.
Каждым своим ходом рыцарь может или продвинуться в сторону соперника на количество клеток, равное своей текущей скорости, или пришпорить лошадь, увеличив скорость на 1, начав двигаться на единицу быстрее.
Максимальная скорость рыцарей равна шести. Ходы делаются по очереди. Выигрывает тот, кто своим ходом приблизился к противнику вплотную, или прошёл ещё дальше.
У первого игрока существует выигрышная стратегия. Попробуйте её найти, сыграв в компьютерную версию этой игры.
Скачать игру “Рыцарский турнир” 1.0
|
Метки: математика турнир игра стратегия |
Как правильно готовиться к математической олимпиаде Кенгуру |
Начинать подготовку к олимпиаде стоит в сентябре, а то и раньше. Как часто слышишь после математических олимпиад разных уровней от участников, не уделивших должного внимания подготовке: «Ну всё, прихожу домой и к олимпиаде следующего года начинаю готовиться серьёзно!». К сожалению, зачастую это лишь красивые слова.
Но готовиться к олимпиаде – не значит целыми днями сидеть, обложившись книгами, и зубрить решения всех задач, которые появлялись ранее. Нужно просто держать себя в форме: быть в курсе основных типов задач, методов их решения и время от времени проверять себя. Впрочем, то, что вы читаете эти советы уже говорит о том, что математика вам интересна и вы следите за новостями из её мира.
Так что вам, во-первых, стоит просмотреть задачи прошлых лет. На нашем сайте периодически выкладываются пакеты задач Кенгуру 3-го, самого высокого уровня различных тематик. Кроме того, повторите материал, наиболее часто встречающийся в заданиях своей возрастной группы. Это, прежде всего – логика, а также:
- Уровень «Выпускник»: комбинаторика, геометрия, функции и графики
- Уровень «Юниор»: теория чисел, геометрия, уравнения с параметрами
- Уровень «Кадет»: числовые последовательности, решение уравнений в целых числах, площади фигур
- Уровень «Школьник»: текстовые задачи, часы и календарь, числовые ребусы
- Уровень «Малыш»: дроби, текстовые задачи, задачи по графическому материалу
В день перед олимпиадой стоит отдохнуть, почитать развлекательную книжку, погулять на свежем воздухе. Пусть накопленные знания улягутся в голове, чтобы назавтра прийти вам на помощь в нужную минуту. И, конечно же, перед олимпиадой нужно как следует выспаться.
На олимпиаде ведите себя спокойно. Помните, что все задачи конкурса проходили отбор жюри, и нерешаемых среди них нет. Внимательно читайте условия, убедитесь, что вы не упустили или не додумали самостоятельно какие-то его факты. Не торопитесь закрашивать ответы в бланке – выпишите их сначала на черновике. Часто можно воспользоваться тем, что олимпиада проводится в форме теста: для некоторых задач решение можно найти перебором пяти вариантов. Не торопитесь сдавать решение до истечения 75-ти минут, лучше ещё раз его проверьте.
После олимпиады возьмите свой листок с условиями и задайте эти задачи родственникам и одноклассникам, не принимавшим в ней участие.
Результаты олимпиады, как правило, объявляются на последнем звонке.
Успехов вам!
|
Метки: математика олимпиада кенгуру |
О сумме цифр, обобщённом признаке делимости и одной нерешённой задаче |
Возьмём какое-нибудь натуральное число, скажем, 17. Сумма его цифр равна 8. Если 17 умножить на 2, получим 34 и сумма цифр этого числа окажется равной 7. А у произведения 17*3=51 сумма цифр равна 6. Вопрос: на какое натуральное число нужно умножить 17, чтобы сумма цифр произведения была наименьшей?
Понятно, что сумма цифр, равная 1 будет только у степеней десятки, которые кратны лишь произведениям степеней двойки и пятёрки. Поэтому попробуем найти кратное 17-ти число вида 100…01 с суммой цифр, равной двум.
17*X=100…01
Чтобы последней цифрой произведения была единица, последней цифрой неизвестного множителя должна быть тройка. Далее, т.к. 17*3=51, а предпоследняя цифра произведения равна 0, то предпоследней цифрой неизвестного множителя должна быть пятёрка.
17*53=901
Третьей с конца цифрой множителя снова должна быть тройка (чтобы произведение оканчивалось на ..001)
17*353=6001.
Далее находим, последовательно:
17*2353=40001
17*82353=1400001
17*882353=15000001
17*5882353=100000001 (!)
Итак, среди чисел, кратных 17-ти наименьшая сумма цифр, равная 2, будет у числа 100000001=17*5882353.
Возникает второй вопрос: а что было бы, если бы потребовалось найти кратное с минимальной суммой цифр для какого-нибудь другого числа? Почти сразу приходят на ум числа 3 и 9, кратные которых, вследствие соответствующих признаков делимости, не могут иметь суммы цифр, меньшие, чем 3 или 9, соответственно. Но оказывается, что и многие другие числа не имеют кратных вида 100…01.
К примеру, попробуем провести операции, аналогичные проведённым с числом 17, для числа 41.
Если существует такой множитель Х, что 41*Х=100…01, то последняя цифра числа Х равна 1.
41*1=41.
Далее, предпоследняя цифра числа Х должна быть равна 6
41*61=2501
Далее получаем, последовательно:
41*561=23001
41*7561=310001
41*97561=4000001
И тут мы обнаруживаем, что зациклились: далее неизвестный множитель будет продолжать обрастать цифрами 6, 5, 7 и 9, а сумма цифр кратного, равная 2, достигнута не будет.
Итак, какова же минимальная сумма цифр у числа, кратного 41-му?
Чтобы найти ответ, разберёмся сначала с таким понятием, как признак делимости. А именно: почему для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m?
|
Метки: признак делимость задача |
Далеко, далеко, на лугу пасутся ко... |
Задача
Трава на лугу растёт равномерно. Известно, что 30 коров съедают всю траву за 60 дней, а 70 коров – за 24 дня. Сколько коров съедят всю траву на лугу за 96 дней?
Решение
Это одна из красивых арифметических задач, которые хотя и можно решить составлением уравнения, но намного красивее – сделать это с помощью последовательных рассуждений.
Итак, известно, что:
30 коров за 60 дней съедят всё поле и ту траву, которая на нём вырастет за 60 дней
70 коров за 24 дня съедят всё поле и ту траву, которая на нём вырастет за 24 дня.
Следовательно:
Всей травы на поле и той, что вырастет на нём за 60 дней, одной корове хватит на 30*60=1800 дней.
Всей травы на поле и той, что вырастет на нём за 24 дня, хватит одной корове на 70*24=1680 дней.
Отсюда, травы, которая вырастет на поле за 60-24=36 дней, хватит одной корове на 1800-1680=120 дней.
Значит всей травы на поле и той, что вырастет на нём за 60+36=96 дней, хватит одной корове на 1800+120=1920 дней
А то, что одна корова съест за 1920 дней, за 96 дней съедят 1920/96=20 коров.
Ответ
За 96 дней всё поле съедят 20 коров.
|
Метки: математика олимпиада задача арифметика |
Задачи III этапа Всеукраинской олимпиады по математике 2009 |
База задач на сайте пополнилась условиями III (областного) этапа Всеукраинской олимпиады по математике за 2009 год. В качестве примера приводим несколько заданий для различных классов. Испытайте свои силы и получайте удовольствие!
1. В супермаркете введены скидки. За покупку товаров на сумму от 300 гривен, покупатель получает скидку 4%, а при покупке товаров на сумму от 600 гривен, он получает скидку 10%. На какую наибольшую сумму (с точностью до копейки) может приобрести товаров покупатель, если у него в кармане
а) 594 гривен;
б) 534 гривны?
2. Шахматная доска размером 7x7 покрашена в шахматном порядке (все угловые клетки черные). По шахматной доске ходит фишка, которая может ходить с клетки на соседнюю по стороне клетку. Если фишка попадает на некоторую клетку, то эта клетка меняет свой цвет на противоположный. Вначале фишка стоит в левом нижнем углу. Можно ли с помощью перемещения этой фишки перекрасить все клетки доски в черный цвет?
3. Найти наибольшее трехзначное число, которое удовлетворяет такие три условия:
1) само число простое;
2) число, которое записано теми же самыми цифрами в обратном порядке также простое;
3) произведение цифр числа также является простым числом.
4. Все числа от 1 до 2009 возвели в квадрат, после этого полученные числа в произвольном порядке записали в виде одного числа. Может ли полученное число быть квадратом целого числа?
5. Найти наименьшее натуральное число, у которого произведение цифр равно 5120.
6. На бумаге в клеточку выделен квадрат 2009x2009. Два игрока по очереди закрашивают в желтый цвет единичные отрезки, которые являются границами единичных квадратов, которые расположены внутри или на границе выделенного квадрата и еще не были закрашены. Побеждает тот игрок, после хода которого, впервые одна единичная клетка станет иметь покрашенные в желтый цвет сразу все 4 стороны. Кто побеждает в этой игре при правильной игре обоих – тот, кто начинает или тот, кто ходит вторым?
7. Назовем заполнение квадрата 2009x2009, разбитого на единичные квадратики, „правильным”, если он заполнен числами 1, 2, 3, ..., 2009 так, что в каждой строке и в каждом столбике есть каждое из этих чисел. Рассмотрим расстояние от центральной клетки до ближайшей клетки с числом 1 (под расстоянием понимается наименьшее число ходов, которые нужны шахматному королю, чтобы добраться до клетки). Какое наибольшее значение может принимать это расстояние?
Все условия III этапа всеукраинской олимпиады по математике на сайте:
11 класс
10 класс
9 класс
8 класс
7 класс
|
Метки: математика олимпиада задача 2009 |
Число 2009 |
• Число 2009 раскладывается на простые множители следующим образом:
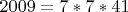
• Следовательно, число 2009 можно представить в виде разности квадратов целых чисел тремя способами:
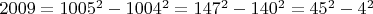
• А в виде суммы квадратов число представляется единственным образом:
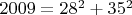
• Чтобы получить число 2009 в виде суммы кубов, потребуется минимум 4 слагаемых, и сделать это можно тремя способами:
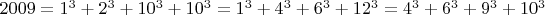
• Как сумму треугольных чисел (имеющих вид
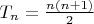 ) число 2009 можно представить 11-ю способами:
) число 2009 можно представить 11-ю способами: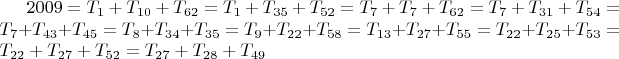
• А в виде разности треугольных чисел число 2009 можно представить 6-ю способами:
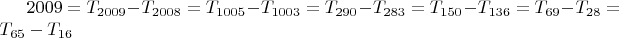
• 2009-е треугольное число равно 2 019 045
• Число 2009 входит в Пифагоровы тройки взаимно-простых чисел: (2009; 2018040; 2018041), (2009; 41160;41209), (360;2009;2041)
• Число 9002, образованное из 2009 обратной записью, также делится на 7:
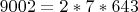
• Число 2009 делится на сумму всех своих делителей, меньших корня из него: 1+7+41=49 и 2009 делится на 49
• 2009-е простое число равно 17471, это палиндром, оно одинаково читается как справа налево, так и слева направо
• Простыми также являются числа
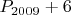 ,
, 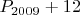 ,
, 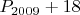 ,
, 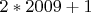 ,
, 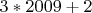 ,
, 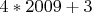
• Рассмотрим процесс: берём натуральное число и прибавляем к нему сумму его цифр. Число 2009 в нём можно получить из самопорождённого (по Капрекару) числа 1693 за 19 шагов: 1693 - 1712 = 1693+(1+6+9+3) - 1723 = 1712+(1+7+1+2) - 1736 - 1753 - 1769 - 1792 - 1811 - 1822 - 1835 - 1852 - 1868 - 1891 - 1910 - 1921 - 1934 - 1951 - 1967 - 1990 - 2009.
• В другом процессе, рассмотренном индийским математиком Капрекаром, будем из числа, образованного цифрами четырёхзначного числа, записанными в порядке убывания, вычитать число, образованное теми же цифрами, но в порядке возрастания. К числу 6174, постоянной Капрекара, мы придём за 3 шага: К(2009) = 9200-0029=9171; К(9171) = 9711-1179=8532; К(8532) = 8532-2358=6174. К(6174) = 7641-1467=6174.
• В числе
 ровно 5765 цифр. Оно заканчивается пятьюстами нулями.
ровно 5765 цифр. Оно заканчивается пятьюстами нулями. • Пожалуй, наиболее экзотический факт: оказывается, существует ровно 2009 5-мерных гексамино.
• Cуществует ровно 2009 Гамильтоновых графов с 8-ю вершинами. (В Гамильтоновых графах между каждыми двумя вершинами существует путь, проходящий через все остальные вершины ровно один раз)
Другие материалы для подготовки к математическим олимпиадам
|
Метки: математика олимпиада 2009 |
Дневник GeneralCFR |
|
|






