-Метки
-Рубрики
- Философия, эзотерика,религия и наука (468)
- Солнце и Земля (361)
- Человеческий организм (344)
- эпифиз (19)
- Позвоночник (15)
- Осознанные сновидения (10)
- зубы (6)
- История (325)
- Тартария (26)
- Русь (286)
- Руны Русского Рода (260)
- Руны Русского Рода (Основы) (47)
- Артефакты (33)
- мои исследования Рун Русского Рода (21)
- Рунная формула Перехода (6)
- Искусство (216)
- О борьбе с паразитом за свою ВОЛЮ (190)
- Интересные книги и произведения (172)
- Порывы души (171)
- Jyj (165)
- Сказ как (146)
- Догода "Книга Божественной Любви" (23)
- сказки от Догоды (16)
- сказки от Jyj (12)
- Когда поют руны ( от Асмик) (11)
- Сила слова и Руский язык (142)
- Полезные мелочи (118)
- Влияние музыки, звука и раскрытие голоса (108)
- нити (107)
- Ви Къ и Го Ръ (91)
- Деревья! (77)
- Космос (55)
- Выживание (Чеурин Г.С и другие) (55)
- В.Пятибрат "Глубинная книга" (53)
- Древняя письменность и скандинавские руны (52)
- Константин Михайлов (51)
- Сказка про Агни и Химу (16)
- "Рудра" К.Михайлов (13)
- Обсуждения того, что волнует (50)
- Тайны и сказки Урала (49)
- Фоменко В.Н (49)
- жизнь (38)
- Кержаки и история рода Белогора (29)
- Мои путешествия (26)
- Ювенальная и гендерная политика: противостояние (25)
- Экология Матери Земли (19)
- Про пирамиды (18)
- Жарникова С.В. (15)
- Доски Судьбы - Октава Души (12)
- Х.Аргуэльес "Зонд с Арктура" (11)
- Зепп Хольцер и уход за растениями (9)
- Х.Аргуэльес "Скользящие по волнам Зувуйи" (5)
- Кольцов И.Е (4)
-Ссылки
-Цитатник
Загадочная подземная цивилизация Ктонов 28 февраля 2003 года на шахте, расположенной близ город...
Знамя, несущее и храняшее Любовь. - (0)Знамя, несущее и храняшее Любовь. Я тут всё думала, почему мне нравится знамя СССР...
Гипотеза про Искусственный интеллект, Землю и человечество. - (0)Человек разрушил экосистему, и скоро на планете станет невозможно жить Shutterstock Искусственный...
10 правил манипулирования обществом от Ноама Хомский - (0)«Говорите с человеком так, как будто ему 12 лет...» 10 правил манипулирования обществом «Говорите...
Он умер трижды и увидел тайны Вселенной. Сенсационное путешествие во времени японского астронома - (0)Он умер трижды и увидел тайны Вселенной.Сенсационное путешествие во времени японского астронома ...
-Новости
Уральские туристы обнаружили в горах огромную пирамиду: она в несколько раз больше пирамиды Хеопса - (6)
Ученые показали реальную фотографию черной дыры. Что нужно знать о снимке века? - (1)
на Урале учёные нашли орудия, возраст которых, предположительно, достигает 100 тысяч лет. - (0)
-Музыка
- Помни, не позабудь. (из м/ф Исчезновение Харухи Судзумии)
- Слушали: 197 Комментарии: 0
- Вивальди. Зима
- Слушали: 4448 Комментарии: 0
- Любовь остаётся... (Михей и Инна Стил)
- Слушали: 446 Комментарии: 0
- Richard Clayderman - Romeo & Juliet
- Слушали: 12382 Комментарии: 0
- Roxette - Listen To Your Heart (pod fortepiano)
- Слушали: 509 Комментарии: 0
-Всегда под рукой
-Подписка по e-mail
-Поиск по дневнику
-Статистика
Ау! Математики!!! Кто поможет решить уравнения? |
Ну ведь должны же они обитать на Лиру , не всё жъ ЛиРикам)))
На самом деле нужна помощь именно с математической точки зрения. Хотя бы идеи.
Помогите решить рунные уравнения, пожалуйста! Хотя бы вот эти?
А вообще для понимания Рун Русского Рода через математические уравнения были даны следующие условия и подсказки:
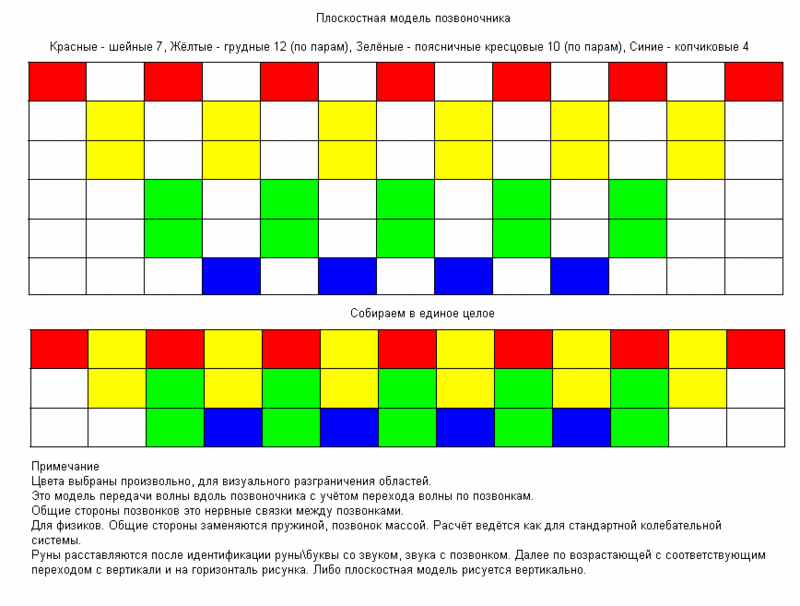
1. Дана плоскостная модель позвоночника,
где синим - позвонки копчика (4), зелёным - позвонки пояснично-крестцового отдела (10), жёлтым - грудные (12), красным - шейные (7)
Все вместе они сворачиваются в рунную матрицу-полусоту-скрижаль, тогда можно увидеть - как происходит взаимное влияние волны между позвонками.
"Получившаяся структура – перевёрнутая усечённая пирамида и есть плоскостная модель позвоночника. В этом виде позвоночник предстаёт перед нами как жёсткая и взаимосвязанная система. Три слоя системы – группы позвонков неразрывно связаны друг с другом.
Всякий, кто практикует массаж, скажет, что массирование позвонков шеи оказывает расслабляющее действие на весь организм.
Из плоскостной модели позвоночника видно, что в первом слое позвонки шеи охватывают часть позвонков 2 Группы. Воздействуя механически (массируя) на шейные позвонки энергия этого воздействия передаётся на часть 2 Группы позвонков (грудных), те в свою очередь на 2 слой и так далее до копчиковой группы."
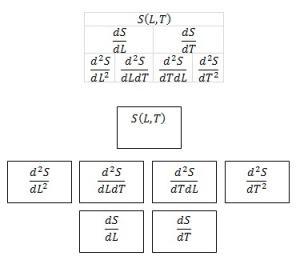
На нижней схеме, каждый блок соответствует "черте" исходной матрицы.
А потом, используя "метод размерностей" написать сколько-нибудь дифуров. Например 35.
Решить их и посмотреть на эти решения.
Если за каждой руной скрыт некий динамический процесс, то его можно описать соответствующим уравнением. Один из вариантов, воспользоваться функциями, которые этот процесс могут описывать. К этим функциям можно отнести саму функцию, скорость её изменения и скорость изменения скорости, т.е. проще говоря ускорение.
В таблице эти функции даны.
Один из вариантов получения уравнения это прировнять мультипликативную форму записи четырёх звенной руны с мультипликативной формой записи трёх звенной руны умноженной на безразмерный коэффициент - К. Такой вариант напрашивается сам собой, так как четырёх звенных рун 35 и трёх звенных 35.
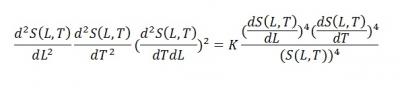
(d^2 S(L,T))/(dL^2 ) (d^2 S(L,T))/(dT^2 ) 〖((d^2 S(L,T))/dTdL)〗^2=K (〖(dS(L,T)/dL)〗^4 〖(dS(L,T)/dT)〗^4)/〖(S(L,T))〗^4
Это уравнение МОЖЕТ описывать руну под номером 24.
Уравнение надо хотя бы одно решить (это я по поводу рунных), может вам ещё одна золотая гармония откроется."
Для 4
Кто нибудь пробовал решить?
А то так получается как в тёмной комнате беседа на троих, глухого с немым в присутствии слепого.
Для 24 решается достаточно просто, а с 4 повозиться надо.
Если каждой руне стихия соответствует и описывает некое её свойства, то это хорошо видно в функциях, которые являются решениями этих уравнений.
Причём без всякой "эзотерической мути" и перста в тьму невежества указывающего.
[S]*[S/L^2]*[S/L]*[S/T]
Преобразуйте, получите: S^(4)*L^(-3)*T^(-1).
Далее выпишите уравнение в мультипликативном виде для соответствующего трех звенного вида, только возведите сразу в некую степень каждый множитель, который далее определится, из системы уравнений:
Получим
[S/L/T]^x*[S/T/L]^y*[S/T^2]^z
Преобразуйте, получите: S^(x+y+z)*L^(-x-y)*T^(-x-y-2z)
Чтобы ваше уравнение имело физический смысл, необходимо чтобы значения степеней при одинаковых основаниях были равны. Иначе у вас может получится так, что метры равны килограммам. В 19 веке французы используя этот метод хотели все законы физики вывести.
Таким образом, у вас получается
При S уравнение 4 = x+y+z
При L уравнение -3 = -x-y
При T уравнение -1 = -x-y-2z
Решая эту систему уравнений получим
x=3 - y
z=1
Подставляем в конструируемое дифференциальное уравнение, только не забудьте ввести безразмерный коэффициент (это число, и как правило значение его, определяется отдельно), и то что дважды дифференцируемые функции сначала по L потом по T, равны … сначала по Т, потом по L. Если правильно сделаете показатель степени не определённый из системы y исчезнет.
Алгебраические выкладки, это процесс, а физика (как наука о природе) это уравнения (её описывающие) и понимание их сути.
Уравнение Шредингера написано в начале прошлого века, а количество процессов которые оно описывает растёт с каждым десятилетием.
Так что и в этом случае похожая история будет.
Надо для понимания физики детерминировать понятия S,L,T. Посмотреть на решение. Исследовать его. Много чего надо, чтобы ответить на поставленный вопрос.Не всё так сразу и быстро. Это у да Винчи всё просто, он гений, а мы простые смертные (ещё ежика за пазуху засунуть ближнему наровим). Давайте хотя бы выпишем все эти уравнения (35 штук), решим их... и так далее, так далее.
По поводу метода... Решать надо сначала методом разделения переменных. Он не имеет отношения к тому о чём вы сказали, он прост и надёжен, вот только то что получается в результате тоже требует своего подхода.
Если кратко о методе разделения переменных, то надо в уравнение поставить вместо S(L,T)=A(L)*B(T), запустить эту подстановку в исходное уравнение и разнести по обе стороны от знака равенства переменные и функции от них, должно быть что-то типа этого F1(L)=F2(T). Так как размерности разные в этом равенстве то оно будет справедливо только при условии если правая и левая части постоянные (безразмерные) величины. Ну а потом решать каждую часть по отдельности, как просто дифур от одной переменной.
Чтобы проверить себя на наличие возможной ошибки, найденные значения степеней подставьте в уравнение для размерностей, если все размерности сократятся, и получиться 1=1, то определили степени верно, смело можно выписывать с найденными значениями дифур.

S30=S20
S18=S28
А S27 переходит в S12 если в них поменять местами L и T.
Интересно получается, что руны 30 и 20, 18 и 28 различны по начертанию, а функции имеют одинаковые. Т.е. суть рун (30 и 20) и (18 и 28) от направления их записи не меняется.
Некий аналог фразы: То что внизу то и сверху, малое в большом, большое в малом.
Без разницы лево или право, верх или низ. Т.е. некие руны, которыми фиксируется только "направление", без изменения сути.
Суть руны 12 переходит в суть руны 27 и обратно, если в описывающей их функцию L поменять местами с T и наоборот. Какие-то руны "перевёртыши".
Аналог аддитивного закона: От перестановки слагаемых сумма не меняется.
Т.е. если у нас имеется некая "событийная" функция в которой в качестве переменных выступает одна "пространственная" переменная и одна "временная" переменная, то смена в этой функции "пространства" на "время" и наоборот, приводит к разным событиям. В отличие от аддитивного закона. Различие в начертании этих рун (12 и 27), скорей всего говорит о том, что сохраняется сам алгоритм действия, но изменяются объекты с которыми эти действия производятся. Какая-то осевая симметрия. Как координатная сетка, смена осей абсцисс и ординат при повороте относительно оси 45 градусов идущей из нулевой точки.
"Особое внимание следует остановить на докладе Овсепяна Ф.А. «Новые теоретические результаты о пространстве и времени». Там как раз говориться о уравнении решение которое было дано в квадратурах…."
-----------------------------
http://www.liveinternet.ru/users/gm...6314/page2.html
Jyj "Даю вам ссылку на сам текст доклада Овсепяна Ф.А.
О несостоятельности концепции четырёхмерного пространства времени
Хочу сказать, что при моделировании не нужно забывать, что объект и его модель не тождественны во всём."
http://carrier-001.narod.ru/books/1842.pdf
Серия сообщений "Рунная формула Перехода":
Часть 1 - Ау! Математики!!! Кто поможет решить уравнения?
Часть 2 - Ура! Потихоньку уравнения рунные решаются! Помогайте!!!)))
Часть 3 - Рунная формула Перехода. 35 дифференциальных уравнений.
Часть 4 - Рунная формула Перехода. Ещё один шаг к решению.
Часть 5 - Уравнения Рун Русского Рода (моё сегодняшнее их видение)))
Часть 6 - Руский слоговый язык как основа для создания других языков.
| Рубрики: | Руны Русского Рода Jyj Ви Къ и Го Ръ |
Процитировано 5 раз
Понравилось: 1 пользователю
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |
http://gukitkafmi.narod.ru/files/INShitov/string.pdf
читать:
4. Решение уравнения колебаний
конечной струны методом Фурье
Закрепленная на концах струна является источником звука мно-
гих музыкальных инструментов. Струнные музыкальные инстру-
менты известны с древних времен (арфа, лира, кифара и другие).
На протяжение тысячелетий эти инструменты развивались и совер-
шенствовались. Создателями инструментов и музыкантами опыт-
ным путем были выявлены некоторые закономерности и свойства
звучащей струны. Теоретические исследования в этом направлении
начались только в XVIII веке.... и далее
а также для более продвинутых математиков http://eqworld.ipmnet.ru/ru/library/books/ZajcevPolyanin2009ru.pdf:
Глава 1. Метод разделения переменных в линейных
уравнениях (метод Фурье)
Я только главы выделила, которые по нашей теме, так как оттуда уравнения плохо копируются.. ((
http://de.ifmo.ru/--books/0051/1/1_3/14_ex.htm
то есть я так поняла, что когда руна=струне натянутая по определённой траектории, в нашем случае это вид самих рун (35 вариантов), то получаем частоту и форму колебания или звук=аккорд руны?