Интервью с Джоном Шварцем, 23 декабря 1997 г.

   Для читателя, имеющего математическую подготовку, заметим, что мы ставим в соответствие многообразию Калаби–Яу конечную нетривиальную фундаментальную группу, порядок которой в некоторых случаях определяет знаменатель дробного заряда.

   Интервью с Эдвардом Виттеном, 4 марта 1998 г.

   Для читателей, хорошо знакомых с рассматриваемыми вопросами, заметим, что некоторые из этих процессов нарушают закон сохранения лептонного числа, а также CPT-симметрию (инвариантность относительно изменения знака заряда, чётности и направления времени).

   Отметим для полноты, что хотя большая часть приведённых выше аргументов в равной степени справедлива как для открытых струн (струн со свободными концами), так и для замкнутых струн (которым мы уделяли основное внимание), в рассматриваемом вопросе два типа струн могут, кажется, проявлять различные свойства. Действительно, открытая струна не может быть «насажена» на циклическое измерение. Тем не менее, в результате исследований, сыгравших в конце концов ключевую роль во второй революции суперструн, Джо Польчински из Калифорнийского университета в городе Санта-Барбара и двое его студентов, Джиан-Хюи Дай и Роберт Лей, в 1989 г. продемонстрировали, что открытые струны прекрасно вписываются в схему, которая будет описана в данной главе.

   Чтобы ответить на вопрос о том, почему возможные энергии однородных колебаний равны целымкратным 1/R, достаточно лишь вспомнить обсуждение квантовой механики (в частности, примера с ангаром) в главе 4. Там мы узнали о том, что согласно квантовой механике энергия, как и деньги, существуют в виде дискретных порций, т. е. в виде целых кратных различных энергетических единиц. В случае однородного колебательного движения струны во вселенной Садового шланга эта энергетическая единица в точности равна 1/R, как объясняется в основном тексте на основе соотношения неопределённостей. Таким образом, энергия однородных колебаний равна произведению целых чисел на 1/R.

   Математически равенство энергий струн во вселенной с радиусом циклического измерения R или 1/Rесть следствие формулы для энергии υ/R + ωR, где υ — колебательное число, а ω — топологическое число. Данное уравнение инвариантно относительно одновременных взаимных замен υ на ω и R на 1/R, т. е. при перестановке колебательных и топологических чисел с одновременной инверсией радиуса. 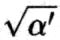Мы используем планковские единицы, но можно работать и в более привычных единицах, если переписать формулу для энергии через так называемую струнную шкалу , значение которого примерно равно планковской длине, т. е. 10⁻³³ сантиметра. В результате энергия записывается в виде выражения υ/R + ωR/α', инвариантного относительно взаимной замены υ на ω иR на α'/R, где последние две величины выражены в стандартных единицах расстояния.

   У читателя может возникнуть вопрос, каким образом с помощью струны, намотанной вокруг циклического измерения радиусом R, можно измерить значение радиуса 1/R. Хотя этот вопрос совершенно правомерен, ответ на него, в действительности, заключается в том, что сам вопрос сформулирован некорректно. Когда мы говорим, что струна намотана на окружность радиуса R, мы с необходимостью используем определение расстояния (чтобы фраза «радиус R» имела смысл). Однакоэто определение расстояния относится к модам ненамотанной струны, т. е. к колебательным модам. С точки зрения этого определения расстояния (и только этого!) конфигурация намотанной струны выглядит так, что струна обёрнута вокруг циклической компоненты пространства. Однако с точки зрения другого определения расстояния, соответствующего конфигурациям намотанных струн, топологические моды точно так же локализованы в пространстве, как и колебательные моды с точки зрения первого определения, и радиус, который они «видят», равен 1/R, что и отмечено в тексте.
   Эти пояснения дают некоторое представление о том, почему расстояния, измеренные с помощью намотанных и ненамотанных струн, обратно пропорциональны друг другу. Однако, так как данный момент достаточно тонкий, возможно, имеет смысл привести технические подробности для читателя, склонного к математическому образу мышления. В обычной квантовой механике точечных частиц расстояние и импульс (по существу, энергия) связаны преобразованием Фурье. Иными словами, собственный вектор оператора координаты 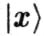 на окружности радиусом R можно определить как 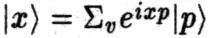, где p = υ/R, а  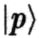есть собственный вектор оператора импульса (прямой аналог того, что мы называли общей колебательной модой струны — движение без изменения формы). В теории струн, однако, есть ещё один собственный вектор оператора координаты 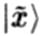, определяемый состояниями намотанной струны: 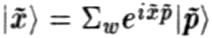, где 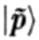 — собственный вектор для намотанной струны с 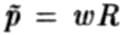. Из этих определений немедленно следует, что xпериодична с периодом 2πR, а  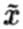периодична с периодом 2π/R, так что x есть координата на окружности радиусом R, а  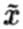— координата на окружности радиусом 1/R. Более конкретно, можно рассмотреть два волновых пакета  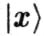и 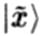, распространяющихся из начала координат и эволюционирующих во времени, с помощью которых можно дать практическое определение расстояния. Радиус окружности, измеренный с помощью каждого из пакетов, будет пропорционален времени возвращения пакета в исходную точку. Так как состояние с энергией E эволюционирует с фазовым множителем, пропорциональным Et, видно, что время, а, следовательно и радиус, равны t ~ 1/E ~ R для колебательных мод и t ~ 1/E ~ 1/R для топологических мод.

   Для читателя, сведущего в математике, отметим, что число семейств колебательных мод струны равно половине абсолютного значения эйлеровой характеристики многообразия Калаби–Яу, как указано в примечании ^{83}. Эта величина равна абсолютному значению разности h^2,1 и h^1,1, где h^p,qобозначает число Ходжа (p,q). С точностью до константы эти значения равны числу нетривиальных гомологий 3-циклов (трёхмерных отверстий) и числу гомологий 2-циклов (двумерных отверстий). Таким образом, хотя в основном содержании говорится о полном числе отверстий, более точный анализ показывает, что число семейств зависит от абсолютного значения разности между числами чётномерных и нечётномерных отверстий. Выводы, однако, те же самые. Например, если два пространства Калаби–Яу отличаются перестановкой соответствующих чисел Ходжа h^2,1 и h^1,1, то число семейств частиц — полное число отверстий — не изменится.