Сегодня был мегазабавный день. Сначала было все было как обычно, но к шестому уроку я начал понимать что уже устал и задолбался и что вообще давно бы пора домой. Я всетаки кое как досидел 2 литературы, закончился восьмой урок и тут ко мне в голову приходить мысль... Оч нехорошая и нерадостная мысль... Мысль о том что еще не пора идти домой, и о том что сейчас будет еще девятый урок - танцы!! Эти гребанные танцы под какуюто странную музыку, эти дурацкие 3 цыфры, раз, два, три, раз, два, три... Я задолбалсо учиться танцевать этот гребанный вальс, Обьясните зачем просирать единственный мой свободный и любимый четверг, когда я не иду ни к репиту, ни на курсы... это ппц. Теперь я должен ходить туда и просирать на это свой последний свободный день, вот так.

я тут начал писать билеты к колку по алгебре...
их 28 а я пока осилил токо 3))))



Билет 1
Определение комплексного числа. Действия с комплексными числами: сложение, умножение, сопряжение, деление. Алгебраическая форма комлексного числа. Тригонометрическая фора комплексного числа. Умножение комплексных чисел в тригонометрической форме. Формула Муавра.

Определение комлексного числа.

Это расширение множества вещественных чисел (С). Любое комплексное число может быть представленно в виде суммы x + iy, где x и y - вещественные числа, i - мнимая единица, то есть одно из чисел, удоволетворяющих уравнению i^2 = - 1.

Действия с комплексными числами.

Формально, комплексное число z  - это пара чисел (x,y) с которыми можно производить операции сложения и умножения таким способом:
сложение:
(x,y) + (x',y') = (x + x', y + y')

умножение:
(x,y)*(x',y') = (xx'- yy', xy' + yx')

сопряжение:
 Свойства сопряженных чисел

деление:
Если делимое и делитель даны не в тригонометрической форме, а в виде
a₁ + b₁i
и
a₂ + b₂i
, то выражая в формуле (9) модули и аргументы через
a₁, a₂, b₁, b₂, получим следующее выражение для частного:



Алгебраическая форма комлексного числа.

Запись комплексного числа z в виде x + iy, , называется алгебраической формой комплексного числа.

Тригонометрическая форма комплексного числа.

Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент (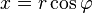, 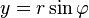), то комплексное число z можно записать в тригонометрической форме

.

Умножение комплексных чисел в тригонометрической форме.

Пусть теперь нам даны комплексные числа
и 
. Давайте их
перемножим:

	Или словами - при умножении комплексных чисел их модули перемножаются а аргументы складываются.

Формула Муавра.

Формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

,

где r — модуль, а  — аргумент комплексного числа.

Или словами - при умножении комплексных чисел их модули перемножаются а аргументы складываются.