-Рубрики
- Путешествия учат больше, чем что бы то ни было... (142)
- Архитектура, как музыка в камне, звучит в веках... (131)
- Львов - это маленький Париж... (78)
- Женщина (62)
- Есть книги, из которых можно узнать обо всем... (51)
- Скажите мне, как вы любите мои фильмы? (50)
- В жизни, как в фотографии, чтобы проявить характер (41)
- Здоровье (33)
- типологии (21)
- Английский язык (19)
- Трудно отпускает Антарктида (16)
- Музыка - это стенография чувств (14)
- Китай (12)
- Не ходить по лезвию ножа, а по нему скользить... (9)
- Жизнь и сновидения - страницы одной и той же книги (7)
-Музыка
- Carmen Cuesta
- Слушали: 2198 Комментарии: 4
- Tears from the moon
- Слушали: 626 Комментарии: 0
- Enya - Caribean Blue
- Слушали: 1722 Комментарии: 0
- Lara Fabian - "Je t'aime"
- Слушали: 14677 Комментарии: 0
- Cirque du Soleil - Alegria
- Слушали: 638 Комментарии: 0
-Метки
-Подписка по e-mail
-Поиск по дневнику
-Статистика
Записей: 1395
Комментариев: 687
Написано: 3512
Фрактал |

Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.

Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
- Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
- Является самоподобной или приближённо самоподобной.
- Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
- Может быть построена при помощи рекурсивной процедуры.
Многие объекты в природе обладают фрактальными свойствами, например побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Содержание |
История
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Примеры
Самоподобные множества с необычными свойствами в математике
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:
- множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины.
- треугольник Серпинского и ковёр Серпинского — аналоги множества Кантора на плоскости.
- губка Менгера — аналог множества Кантора в трёхмерном пространстве;
- примеры Вейерштрасса и Ван дер Вардена нигде не дифференцируемой непрерывной функции.
- кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины, не имеющая касательной ни в одной точке;
- кривая Пеано — непрерывная кривая, проходящая через все точки квадрата.
- траектория броуновской частицы также с вероятностью 1 нигде не дифференцируема. Её хаусдорфова размерность равна двум.
Рекурсивная процедура получения фрактальных кривых
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.
Примерами таких кривых служат:
- кривая дракона;
- кривая Коха;
- кривая Леви;
- кривая Минковского;
- кривая Пеано.
- с помощью похожей процедуры получается дерево Пифагора
...
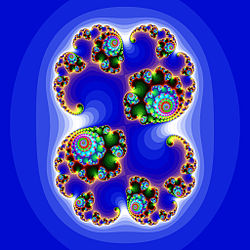
Фракталы в комплексной динамике
Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу XX века и связаны с именами Фату и Жюлиа.
...
Ещё один известный пример такого рода — бассейны Ньютона.
...
Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.
Стохастические фракталы
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:
- траектория броуновского движения на плоскости и в пространстве;
- граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельборта о том, что её размерность равна 4/3.
- эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например в модели Изинга и перколяции.
- различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.
Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, состоящие в получении изображения случайного фрактала.
Применение фракталов
Компьютерная графика
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и т. д.
Анализ рынков
Последнее время Фракталы стали популярны у «трейдеров» для анализа курса фондовых бирж, валютных и торговых рынков.
Физика и другие естественные науки
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Литература
Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста
- неразветвляющееся бесконечное дерево, тождественные самим себе с любой итерации («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…»)
- неразветвляющиеся бесконечные тексты с вариациями («У Пегги был весёлый гусь…») и тексты с наращениями («Дом, который построил Джек»)
В структурных фракталах схема текста потенциально фрактальна
- венок сонетов (15 стихотворений), венок венков сонетов (211 стихотворений), венок венков венков сонетов (2455 стихотворений)
- «рассказы в рассказе» («Книга тысячи и одной ночи», Я.Потоцкий «Рукопись, найденная в Сарагоссе»)
- предисловия, скрывающие авторство (У.Эко «Имя розы»)
- Т.Стоппард «Розенкранц и Гильденстерн мертвы» (сцена с представлением перед королём)
В семантических и нарративных фракталах автор рассказывает о бесконечном подобии части целому
- Х. Л. Борхес «В кругу развалин»
- Х.Кортасар «Жёлтый цветок»
- Ж.Перек «Кунсткамера»
Фрактальные антенны
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка на зданиях внешних антенн. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, а затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.
Сжатие изображений
Существуют алгоритмы для сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо изображения можно хранить отображение сжатия, для которого это изображение является неподвижной точкой.
Децентрализованные сети
Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
Галерея
См. также
- Квазифрактал
- Мультифрактал
- Размер и размерность" class="extiw" href="http://en.wikibooks.org/wiki/ru:_%D0%A0%D0%B0%D0%B7%D0%BC%D0%B5%D1%80_%D0%B8_%D1%80%D0%B0%D0%B7%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C">wikibooks: ru: Размер и размерность
- Алгоритм фрактального сжатия
- Теорема о рекурсивных системах (см. раздел «Высшее руководство»)
Ссылки
Программы для генерации фрактальных изображений
- Incendia — Первый фрактальный генератор в полноценной 3D графике (Donationware);
- Ultra Fractal — пожалуй, самая мощная программа, предназначенная для создания и анимации изображений по фрактальному алгоритму;
- Fractal Explorer — одна из лучших на сегодняшний день программ для создания изображений фракталов;
- XaoS — многоплатформенный генератор фракталов, позволяет приближать и удалять картинку в реальном времени;
- Fractint — очень мощная многоплатформенная программа, развитие которой, к сожалению, давно остановилось;
- Chaoscope — программа трёхмерной визуализации странных аттракторов;
- Apophysis — программа для создания fractal flames. Fractal flames является расширением IFS фракталов;
- RPS/Fract — несложный бесплатный генератор фракталов для платформы Pocket PC (PDA);
- P.Fract — несложный бесплатный генератор фракталов для платформы Palm (PDA);
- EyeFract
- Gnofract 4D
- IFS Illusions — Искусственное искусство программа и галереи
- Sterling2
Сайты о фракталах
- Фрактальные множества — Очень подробная и качественная статья, начиная с комплексных чисел (Санкт-Петербургский государственный университет: ПМ-ПУ)
- Архивохранилище Фрактал опубликовало на USENET
- Фракталы и теория хаоса
- Введение во фракталы
- Доступно о фракталах
- Фракталы в НГУ: описания, форум, программа IFS Builder 3d
- Фракталы от OCo
- Фракталы, как следствие работы алгоритмов в природе
- Красивая жизнь комплексных чисел
- Fractals of aramin (англ.)
- Электронная библиотека по нелинейной динамике — книги о фракталах
- Фракталы, мультифракталы и не только
- Фракталы в литературе: в поисках утраченного оригинала
- Фрактальные системы. Основы теории систем.
- Фракталы Др. Снейка.
- Фрактальная корова в 3D (англ.) — пример с наличием сарказма и исходных кодов для фрактализации объектов в Blender
Литература
- Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.
- Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.
- Федер Е. Фракталы. — М: «Мир», 1991.
- Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.
- Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. — М.: «Мир», 1988.
- Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. — Ижевск: «РХД», 2001.
- Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории.
- Мандельброт Бенуа, Ричард Л. Хадсон (Не)послушные рынки: фрактальная революция в финансах = The Misbehavior of Markets. — М.: «Вильямс», 2006. — С. 400. — ISBN 5-8459-0922-8
Материал из Википедии — свободной энциклопедии
http://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB
Процитировано 1 раз
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |