»гровое управление модел€м в услови€х неполной информации |
(¬ соавторстве с ёлией ‘илимоновой jul305a@gmail.com)
¬ведение
ѕредставьте себе, что летите такой весь победитель на базу, бомб уже нет, и ничего не предвещает бедыЕ

ј тут, скажем, горочка из тумана/облаков выступает неожиданно, или, что несколько хуже, Ч вот этоЕ » вам рады, но исключительно в качестве цели:

#поравалить Ч а вот как это делать с математическим уклоном сейчас и будем разбиратьс€.
ƒа и вообще есть множество случаев, когда необходимо уклонитьс€ от неожиданно возникшей помехи/преграды, нашЋось, как говор€т в яндексе, например.
ќговорка дл€ математиков. »зложение направлено скорее на объ€снение принципов и пон€тность, а не на формальность и строгость. ѕочему так: если интересно - будет мотив разобратьс€ с теорией дифференциальных игр, котора€ лежит в основе, и с первоисточниками, часть из которых перечислена в конце.
„асть перва€ Ч модель в Ђпростых движени€хї
ѕростые движени€ это не то о чЄм в попсе поют, а сама€ проста€ модель динамического объекта, выражаема€ следующей дифференциальной моделью:
где , -управление ограничено
„то это нам даЄт? ≈сли проинтегрировать уравнение, то мы получим траекторию движени€ Ч пр€мую линию
ѕлюс данной модели в еЄ крайней простоте дл€ анализа, минус Ч моделирует она только безынерционные движени€, но это не очень страшно так как моделирование инерционных движений будет выгл€деть (упрощЄнно) как:
и к модел€м соответствующего типа мы перейдем чуть позже.
ќписанна€ модель отражает наши динамические возможности. ƒобавим в нее противника
«десь аналогично ограниченное управление
ѕри этом мы заранее не знаем, где притаилс€ противник, а он, при этом, знает всЄ и ждЄт себе, пока мы подлетим поближе, дл€ того чтобы при помощи своего управлени€
ѕоскольку наша цель Ч всЄ--таки попасть на
ѕри этом, как можно заметить, помеха типа <<гора>> не сама€ страшна€ ситуаци€, так как она неподвижна, хот€ и €вл€етс€ большим преп€тствием, Ч хуже если противник подвижен, поэтому надо обсудить ещЄ пару моментов:
- чтобы иметь возможность уклон€тьс€, мы должны обладать большими динамическими возможност€ми, чем противник, иначе рано или поздно нас поймают, то есть
$inline$Q$inline$ в некотором смысле должно быть меньше$inline$P$inline$ ; - пусть множество помехи, которым управл€ет противник Ч выпуклое, иначе, если примен€ть стратегию уклонени€ <<угол падени€ равен углу отражени€>> Ч можно и не уклонитьс€.
¬оспользовавшись приведенными выше эвристическими рассуждени€ми, посмотрим, как можно решить приведенную выше задачу при следующих услови€х в пространстве
«десь
ѕусть объект начинает движение из точки
ќграничени€ на управлени€
$inline$u(t) \in P \subset \mathbb{R}^2,\ P = S_{1} ([0,\ 0]^{T})$inline$ Ч круг радиуса 1;$inline$v(t) \in Q \subset \mathbb{R}^2,\ Q = S_{0.9} ([0,\ 0]^{T})$inline$ Ч круг радиуса 0.9.
ѕервый игрок стремитс€ перевести траекторию системы за конечное врем€ на терминальное множество
¬рем€ успешного завершени€ игры первым игроком
“раектори€ движени€ системы и компоненты управлени€ первого игрока показаны на следующих рисунках.
“раектори€ движени€ системы.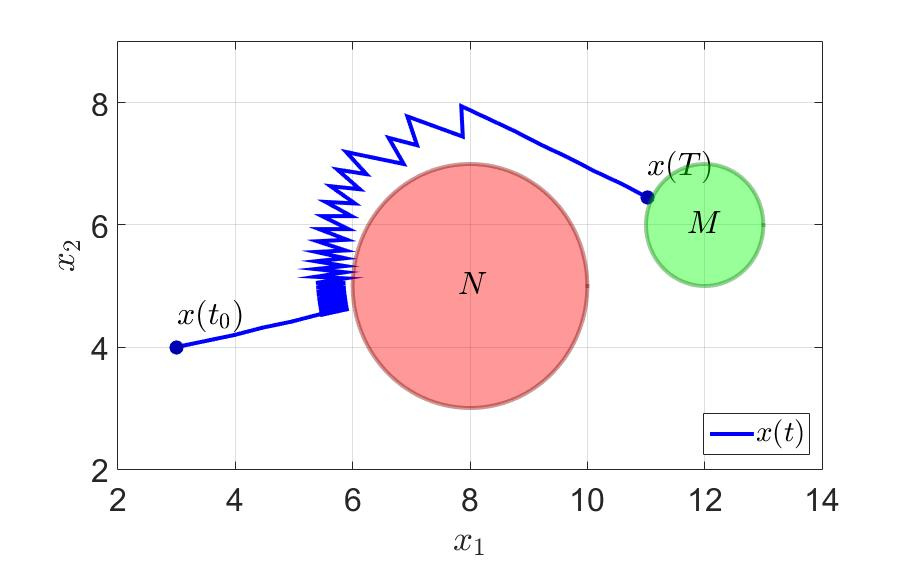
«ависимость первой компоненты управлени€ от времени.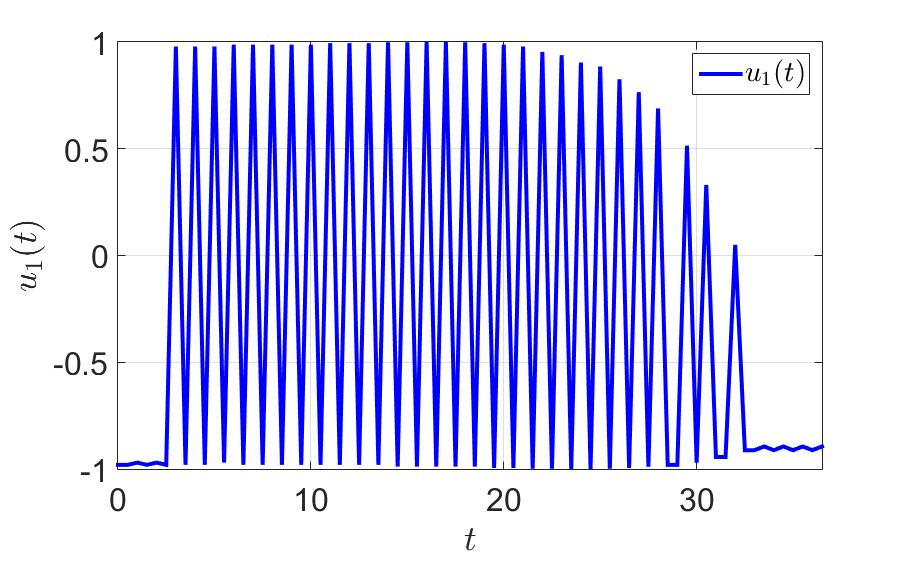
«ависимость второй компоненты управлени€ от времени.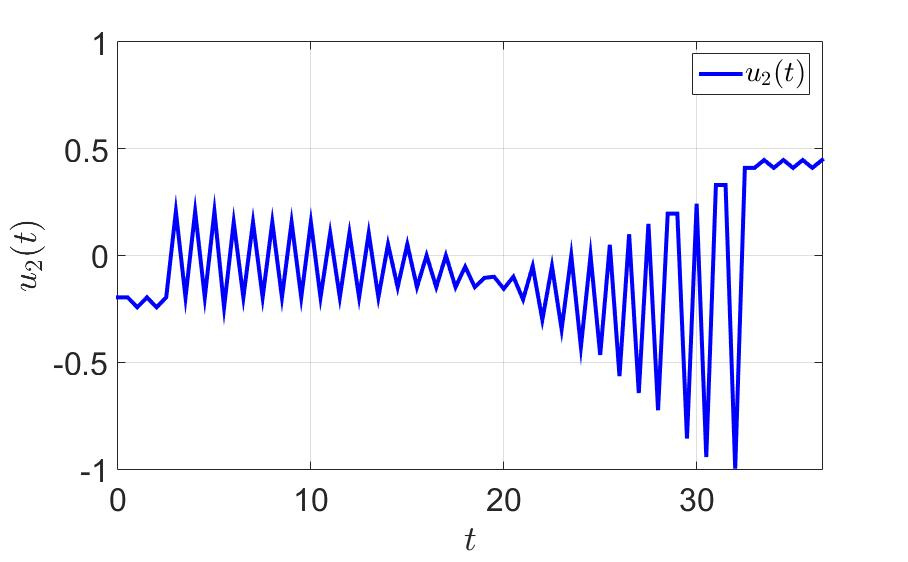
ƒанный подход, очевидно имеет несколько недостатков, а именно:
- большое количество переключений, что плохо с практической точки зрени€, так†как рывки между крайними значени€ми дают существенную нагрузку на органы управлени€;
- как следствие, вместо того, чтобы лететь к цели, мы тратим врем€ на блуждани€, св€занные с уклонением от помехи и наведением на терминальное множество;
- непон€тно, что делать, если мы подлетаем к помехе строго по нормали: уклонение будет проводитьс€ в ту же точку, откуда наводились за шаг до этого Ч то†есть алгоритм может зациклитс€;
- непон€тно, что делать с инерционными объектами, так†как эвристика, конечно, хороша, но реальность несколько сложнее.
„асть втора€ Ч модель всЄ ещЄ в Ђпростых движени€хї, но сокращаетс€ количество переключений
¬виду того, что модель проста€ и позвол€ет нам двигатьс€ по плоскости из любой точки в любую точку (это в дальнейшем будет €вл€тьс€ существенным предположением, а пока просто берЄм на заметку), ничто не мешает нам рассуждать следующим образом.
ƒавайте думать на один шаг вперЄд: если наша система сначала наводилась на цель, а на следующем шаге начала уклон€тс€, то можно найти точку, в которую система придЄт через два шага, и наводитьс€ сразу на неЄ как на промежуточную цель. ћожем? ѕо нашему предположению Ч ƒј.
Ќа том же примере посмотрим, что получаетс€. ¬рем€ успешного завершени€ игры первым игроком сократилось почти в три раза с и вообще полезно дл€ здоровь€.
“раектори€ движени€ системы и компоненты управлени€ первого игрока показаны на на следующих рисунках.
“раектори€ движени€ системы.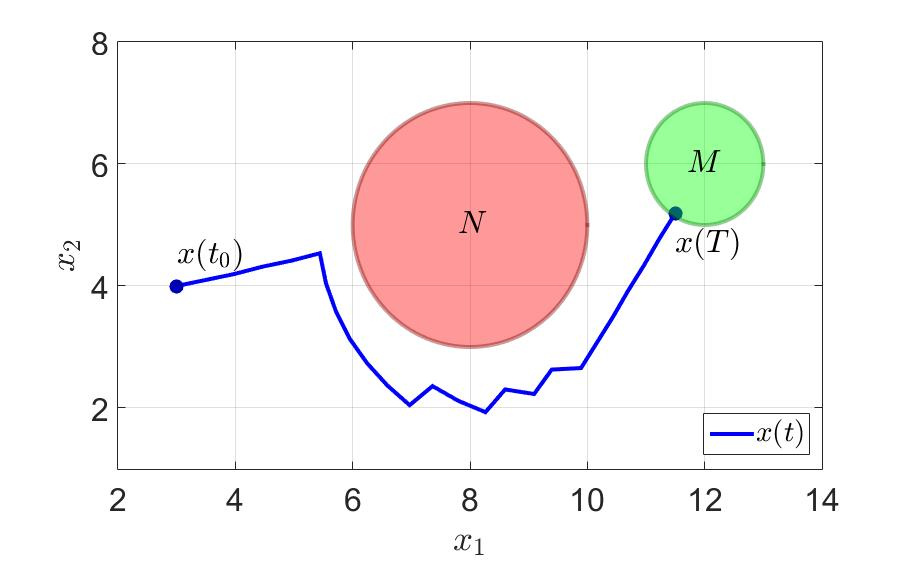
«ависимость первой компоненты управлени€ от времени.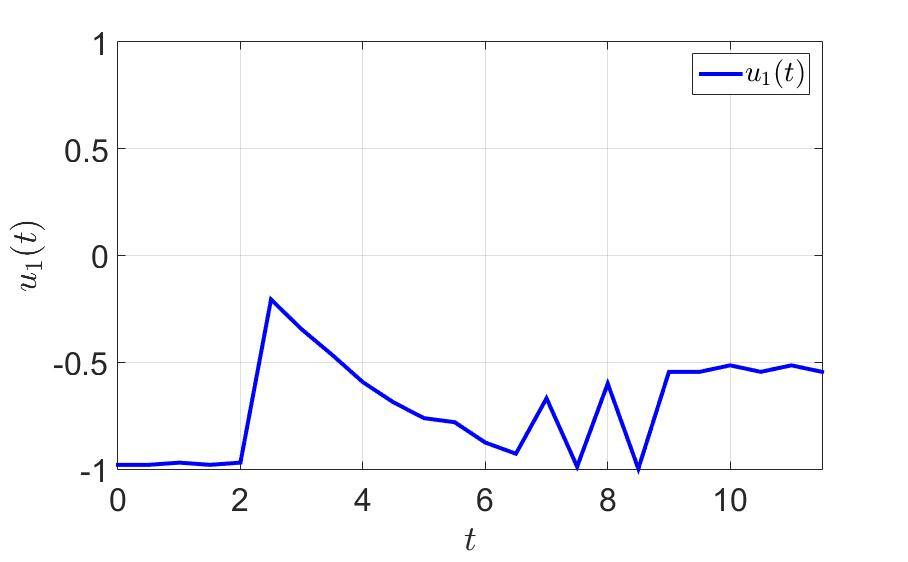
«ависимость второй компоненты управлени€ от времени.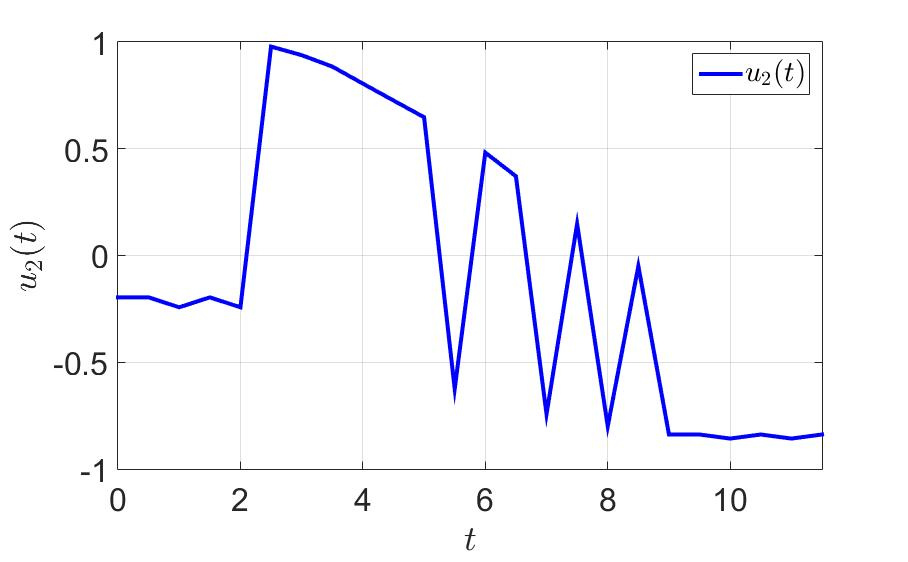
„асть треть€ Ч модель всЄ ещЄ в Ђпростых движени€хї, но теперь решаем вопрос с приближением <<по нормали>>
“ак как мы умеем уклон€тьс€ от одного множества в один момент времени, то ничто нам не мешает построить дополнительное множество таким образом, чтобы, уклон€€сь от него, мы ( возможно с измельчением шага по времени) гарантированно через два шага попадали в точку, отличную от той, в которой находимс€ сейчас. » сделаем мы это следующим образом:
ѕостроение дополнительного множества избегани€ дл€ траектории.
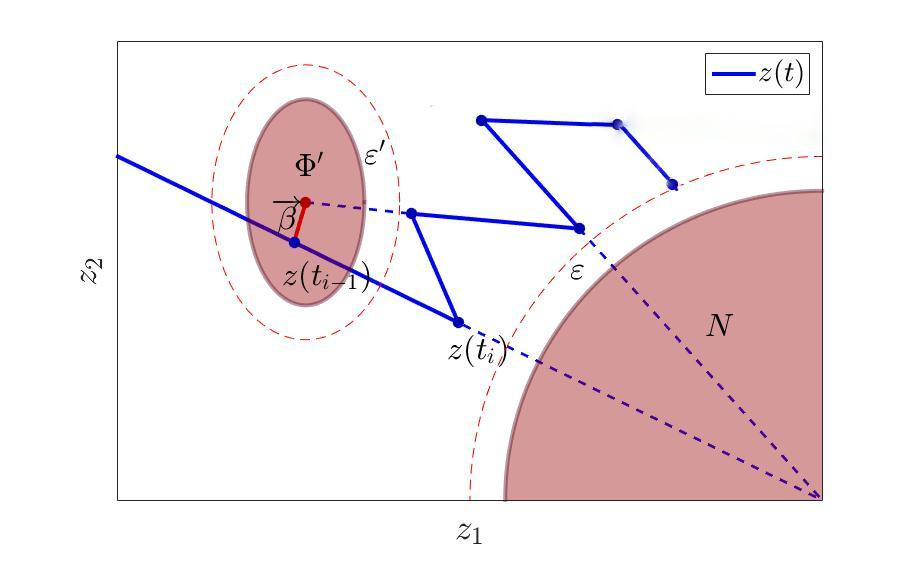
“о есть просто построим дополнительное множество, от которого будем уклон€тьс€, содержащее в себе Ђпроблемнуюї точку не как центр, а с некоторым смещением, как на рисунке.
„асть четверта€ Ч математический базис
ƒл€ того, чтобы построить управлени€ инерционными объектами необходимо всЄ таки погрузитьс€ в теорию, так как простые эвристические рассуждени€ в этом случае работать перестают и, соответственно, необходимо подобрать теоретическую основу решени€. ≈сли у вас жЄсткий приступ лени не хватает времени, то раздел можно, пропустить и воспользоватьс€ сразу результатами, интересующиес€ же Ч смотрим дальше.
¬ качестве основы будем использовать теорию дифференциальных игр, которые в нашей стране развивались Ћьвом —емЄновичем ѕонтр€гиным [1] (если не знаете кто такой Ч об€зательно почитайте, Ћичность с большой буквы, как говоритс€, таких уже не делают) и расовским Ќиколаем Ќиколаевичем [2].
ƒл€ решени€ нам потребуютс€ два множества:
- куда можно попасть первым игроком Ч множество достижимости первого игрока;
- откуда можно завершить преследование вторым игроком первого.
ј также способ их построени€, реализуемый на практике.
— первым множеством, при отсутствии помехи всЄ более или менее пон€тно, если можем построить его таким образом, чтобы включить конечное множество
Ќаведение на множество $M$ в услови€х отсутстви€ помехи.
„то касаетс€ второго множества Ч множества откуда второй игрок может поймать нас и от которого нам и нужно уклон€тьс€, то здесь несколько сложнее Ч следите за пальцами:
- с одной стороны, если мы "приближаемс€" к противнику, то ввиду превосходства наших возможностей, чем мы дальше от него тем веро€тность нас поймать, Ч этому потом придЄтс€ дать строгое объ€снение;
- с другой стороны Ч если мы "удал€емс€" от противника, то ввиду того же самого нашего превосходства противник не сможет нас поймать в любом случае.
“о есть что получаетс€ множество от которого мы уклон€емс€ должно быть с одной стороны большим (при приближении), а с дугой стороны (при удалении) может быть едва превышающим то, от которого необходимо уклонитьс€?
”клонение от множества 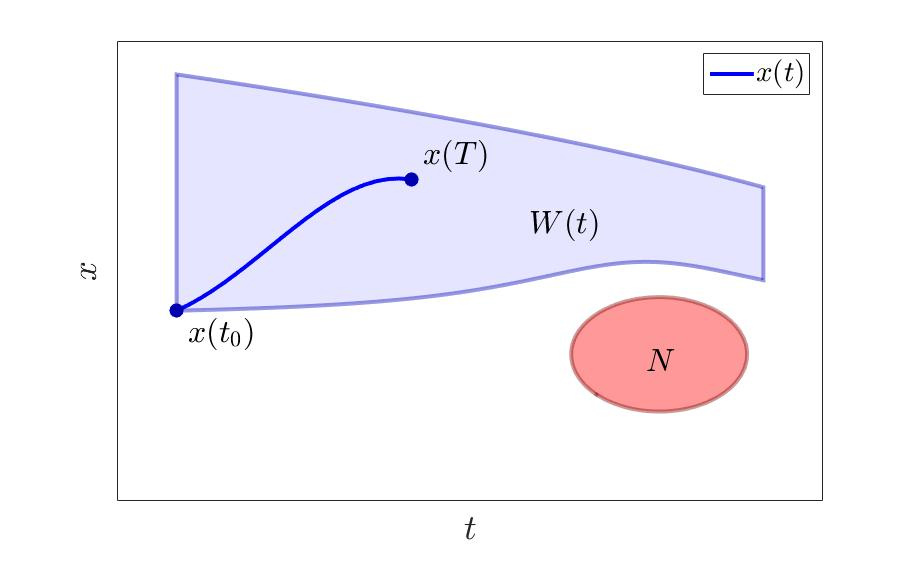
—овпадение? ѕротиворечие? Ќе думаю. ѕодобно ƒоку в "Ќазад в будущее" с его "пространственно-временным континуумом" вспомним, что у нас есть ещЄ одна переменна€ Ч врем€ и будем трактовать термины "приближаемс€" и "удал€емс€" приведенные в кавычках как поведение системы вдоль траектории, что не всегда совпадает с пр€молинейным движением и уж точно не характеризуетс€ рассто€нием в евклидовом пространстве. «ато временем движени€ до конкретной точки пон€ти€ "далеко-близко" и "приближаемс€-удал€емс€" характеризуютс€ очень неплохо.
¬ этом случае давайте будем строить управление уклонени€ не от множества от которого нам надо уклон€тьс€
—оответственно общее управление управление первого игрока так, чтобы в каждый момент времени он решал только одну из этих подзадач.
‘ормализуем теперь движение нашего объекта
где
¬ектор
ƒвижение начинаетс€ при
¬
»гра считаетс€ успешно завершенной первым игроком в момент первого попадани€ точки
Ѕудем отдельно рассматривать дифференциальную игру с точки зрени€ первого и второго игроков.
A: ѕредполагаетс€, что первый игрок знает:
- динамические возможности конфликтно управл€емого объекта
$inline$x$inline$ , то есть матрицы$inline$A,\ B,\ C$inline$ , множества$inline$P,\ Q$inline$ ; - начальное состо€ние игры
$inline$(x_0, t_0)$inline$ ;
ѕредполагаетс€ также, что первый игрок способен обнаружить множество
ќпределим стратегию первого игрока
«адача A: Ќайти начальные состо€ни€
Ѕ:¬торой игрок обладает полной информацией о ходе игры.
ќпределим стратегию второго игрока
«адача Ѕ: Ќайти начальные состо€ни€
Ѕудем считать, что
ѕодраздел 4.1. ƒостаточное условие разрешимости задачи уклонени€ первого игрока от множества $inline$N$inline$
–ассмотрим задачу Ѕ Ч задачу преследовани€ вторым игроком первого и построим дл€ неЄ множество точек, из которого данна€ задача будет иметь решение. “ак вот, дл€ подобного типа задач ѕонтр€гин придумал способ построени€ нужного множества Ч альтернированна€ сумма Ч
»з [6, стр. 69 Ч теорема 17.1] следует, что в этих услови€х можно воспользоватьс€ теоремой об альтернативе:
ƒл€ вс€кой начальной позиции$inline$(t_0, x_0)$inline$ и выбранного$inline$\bar T \ge t_0$inline$ верно одно из двух утверждений:
1) Ћибо найдетс€ стратеги€$inline$\bar{v}$inline$ , котора€ дл€ всех движений$inline$x(t)=x(t,t_0,x_0,\bar{v})$inline$ обеспечит встречу$inline$\{\tau,x(\tau)\}\in N$inline$ за конечное врем€$inline$\tau<\bar{T}$inline$ . “о есть, в классе позиционных стратегий второго игрока разрешима задача преследовани€ (задача Ѕ).
2) Ћибо, в противном случае, найдетс€ стратеги€$inline$\bar{u}$inline$ , котора€ дл€ всех движений$inline$x(t)=x(t,t_0,x_0,\bar{u})$inline$ , обеспечит уклонение от множества$inline$\epsilon$inline$ -окрестности множества $N$ вплоть до момента времени$inline$\bar{T}$inline$ . “о есть, в классе позиционных стратегий первого игрока разрешима задача уклонени€ (задача ј).
ѕри этом, ввиду
€вл€етс€ достаточным условием решени€ задачи уклонени€ первого игрока из начальной позиции
≈сли ресурсы первого игрока, определ€емые множеством
—уществование момента
“о есть можно построить стратегию
—ледовательно, дл€ того, чтобы обеспечить уклонение от множества
ћножество
характеризует минимальное рассто€ние между преследователем и убегающим в момент времени
», если насто€щие математики на некоторое врем€ закроют глаза, так как следующее рассуждение €вл€етс€ ооочень частным случаем, то на пальцах это выгл€дит следующим образом: пусть множество помехи у нас шарик радиуса 5, множество управлени€ шарик радиуса 2, а помехи -- соответственно 1, тогда врем€ за которое мы должны обнаруживать помеху никак не должно быть меньше 4. ћатематики могут открывать глаза.
јналогичным образом можно решить задачу наведени€ на множество
ѕодраздел 4.2. ѕостроение управлени€ первого игрока дл€ решени€ задачи ј
ѕусть первый игрок может заметить множество помехи
“огда возможность перехвата вторым игроком первого (успешного завершени€ задачи Ѕ) в момент
«десь первый мы в момент времени
Ѕудем строить управление первого игрока, счита€, что выполнены следующие предположени€.
Ќа второго игрока наложены следующие ограничени€:
второй игрок никогда не сможет достичь терминального множества
$inline$M$inline$ :
$$display$$\forall T: \Phi( T, \tau) \cap M \neq \emptyset;$$display$$
в противном случае стратеги€ "закрыть собой" обеспечит победу второму игроку;
- начальна€ позици€ игры не принадлежит множеству
$inline$\Phi( T, \tau)$inline$ , откуда возможно успешное завершение задачи Ѕ Ч преследовани€ вторым игроком первого:
$$display$$x(t_0)\notin \Phi( T, \tau),$$display$$
что гаратнирует нас от того, что мы при по€влении откажемс€ внутри множества где нас поймают и игра потер€ет вс€кий смысл.
–ассмотрим задачу уклонени€ первого игрока от множества
$inline$N$inline$ отдельно от задачи наведени€ на целевое множество$inline$M$inline$ .
ѕри этом, если дл€ нашей игры выполнено приведенное выше предположение, то при любом начальном значении
$inline$x_0: x_0 \notin \Phi(\Theta,\tau)$inline$ , можно показать, что существует така€ стратеги€ уклонени€, что рассто€ние между траекторией$inline$x(t)$inline$ и множеством избегани€$inline$\Phi(\Theta,\tau)$inline$ может будет больше$inline$\epsilon$inline$ и зависеть только от хода игры, а не от еЄ начального значени€.
„то, перевод€ с математического на русский, означает, что в зависимости от параметров игры всегда существует ненулевое рассто€ние между нами и множеством из которого нас можно поймать.
ѕри этом, в качестве стратегии уклонени€ можно выбрать управление экстремального сдвига, обеспечивающее, согласно теореме об альтернативе [6, стр. 69], уклонение от множества
$inline$N$inline$ в виде:
$$display$$ U(\theta - t_i, x(\theta - t_i)) \in \underset{u \in P} {\mathrm{argmax}} \left\{ \pi u,\tilde{\psi_i}(x(\theta - t_i)) \right\},$$display$$
где
$$display$$\tilde{\psi_i}(x(\theta-t_i))\in \underset{\psi \in S_1(0)} {\mathrm{argmin}} \left\{ c(\Phi(\Theta,\tau),\psi)-(\pi x(\theta-t_i),\psi) \right\}.$$display$$
“ак как выполн€ютс€ услови€ леммы 15.2 [6, стр. 65], то, повтор€€ еЄ доказательство, получаем нужную оценку дл€ минимального евклидового рассто€ни€ между траекторией
$inline$x(t)$inline$ и множеством$inline$\Phi(\Theta,\tau)$inline$ , котора€ стремитс€ к$inline$0$inline$ при измельчении шага разбиени€ по времени.
–ассмотрим теперь задачу наведени€ траектории системы на терминальное множество
$inline$M$inline$ . ѕри отсутствии каких-либо помех в виде множества$inline$N$inline$ и выполнении услови€ теоремы об альтернативе задача наведени€ разрешима, если начальна€ точка$inline$x(t_0)$inline$ принадлежит множеству управл€емости, а само управление наведени€ будет иметь вид:
$$display$$ U(\theta-t_i,x(\theta-t_i))\in \underset{u \in P}{\mathrm{argmin}}(\pi u,\tilde{\psi_i}(x(\theta-t_i))).$$display$$
Ѕудем строить управление наведени€--уклонени€ в следующем виде:
- определ€ем
$inline$T$inline$ в ходе построени€ альтернированного интеграла, решающего дл€ нашей системы задачу наведени€; - рассматриваем движение системы в момент
$inline$t_i$inline$ ,$inline$i=\overline{0,T}$inline$ .
ѕровер€ем дл€ следующего шага пустоту пересечени€:
$$display$$ \pi (x(t_i) + P) \cap \Phi(\Theta,\tau)$$display$$
- если множество достижимости системы из точки
$inline$x(t_i)$inline$ не пересекаетс€ с множеством$inline$\Phi(\Theta,t_i)$inline$ , то первый игрок выбирает управление наведени€;
- в противном случае первый игрок выбирает управление уклонени€.
ќтметим, что в общем случае условие окончани€ игры наведени€ может быть нарушено, т.е.
$inline$w(t_{i+1})\notin W(T)$inline$ , где$inline$T$inline$ ,$inline$W(T)$inline$ Ч это найденные ранее значени€ времени окончани€ игры и соответствующий ему альтернированный интеграл. ¬ данном случае необходим пересчЄт альтернированного интеграла Ћ.—. ѕонтр€гина$inline$W(T^j)$inline$ и поиск соответствующего ему нового времени окончани€ игры$inline$T^j$inline$ ,$inline$j$inline$ -натуральное число.
ѕримен€€ описанную стратегию, первый игрок в каждый момент времени будет либо наводитьс€ на терминальное множество
$inline$M$inline$ , сокраща€ рассто€ние до него, либо уклон€тьс€ от множества помехи$inline$N$inline$ , не попада€ внутрь него.
ѕоскольку множество
$inline$N$inline$ Ч строго выпуклый компакт, то дл€ его огибани€ по описанной стратегии потребуетс€ конечное врем€, а теорема об альтернативе гарантирует уклонение от множества$inline$N$inline$ в течение конечного времени. ѕоскольку задача наведени€ в услови€х отсутстви€ помехи имеет решение за конечное врем€, то общее врем€ завершени€ игры тоже конечно. ѕри этом
$$display$$ \bar{T}_{min} = T$$display$$
Ч врем€ завершени€ игры не меньше времени наведени€, а
$inline$\bar{T}_{max}$inline$ в общем случае оценить невозможно, хот€ оно и существует.
„асть п€та€ Ч собираем всЄ вместе
ѕроверим теперь на практике, что даЄт построенный способ управлени€ сначала без учЄта снижени€ колчества перекючений, а потом с учЄтом данной оптимизации. ƒл€ чего рассмотрим одну из типовых задач имеющих им€ собственное Ч "ƒва крокодила", моделирующую движени€ двух инерционных объектов с разными динамическими параметрами. —оотвественно пусть теперь первый игрок стремитс€ решить задачу ј.
—оотвествующа€ система дифференциальных уравнений будет иметь вид:
$$display$$\begin{array}{rcl} \dot{x}_1 &=& x_3,\\ \dot{x}_2 &=& x_4,\\ \dot{x}_3 &=& u_1 - v_1,\\ \dot{x}_4 &=& u_2 - v_2. \end{array}$$display$$
«десь
$inline$x_1,\ x_2$inline$ Ч координаты объекта$inline$x$inline$ на плоскости, а$inline$x_3,\ x_4$inline$ Ч компоненты его скорости,$inline$x(t) = [x_1(t),\ x_2(t),\ x_3(t),\ x_4(t)]^{T} \in \mathbb{R}^4;$inline$
объект начинает движение из точки$inline$x(t_0) = [3,\ 4,\ 0,\ 0]^{T} \in \mathbb{R}^4.$inline$
ќграничени€ на управлени€
$inline$u(t),\ v(t)$inline$ имеют вид
$$display$$u(t) = [u_1(t),\ u_2(t)]^{T} \in P \subset \mathbb{R}^2,\ P = S_{1} ([0,\ 0]^{T}),$$display$$
$$display$$v(t) = [v_1(t),\ v_2(t)]^{T} \in Q \subset \mathbb{R}^2,\ Q = S_{0.9} ([0,\ 0]^{T}).$$display$$
ѕервый игрок стремитс€ перевести траекторию системы за конечное врем€ на терминальное множество
$$display$$M = S_{1}([12,\ 6]^{T}),$$display$$
избежав при этом попадани€ на множество помехи
$$display$$N = S_{2}([8,\ 5]^{T}).$$display$$
¬ случае если первый игрок не занимаетс€ снижением количества переключений, то врем€ завершени€ игры будет
$$display$$T = 22,30.$$display$$
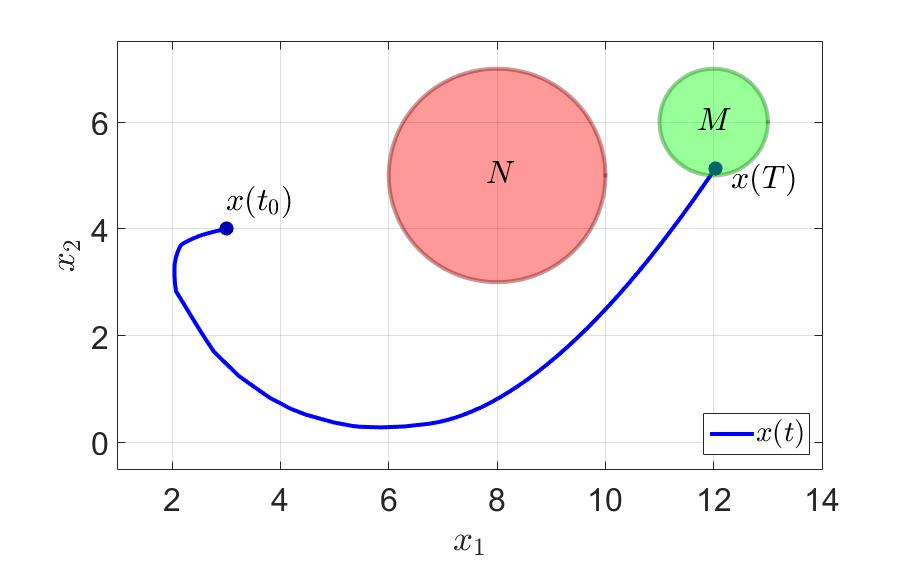
“раектори€ движени€ системы и компоненты управлени€ первого игрока показаны на следующих рисунках.
“раектори€ движени€ системы.
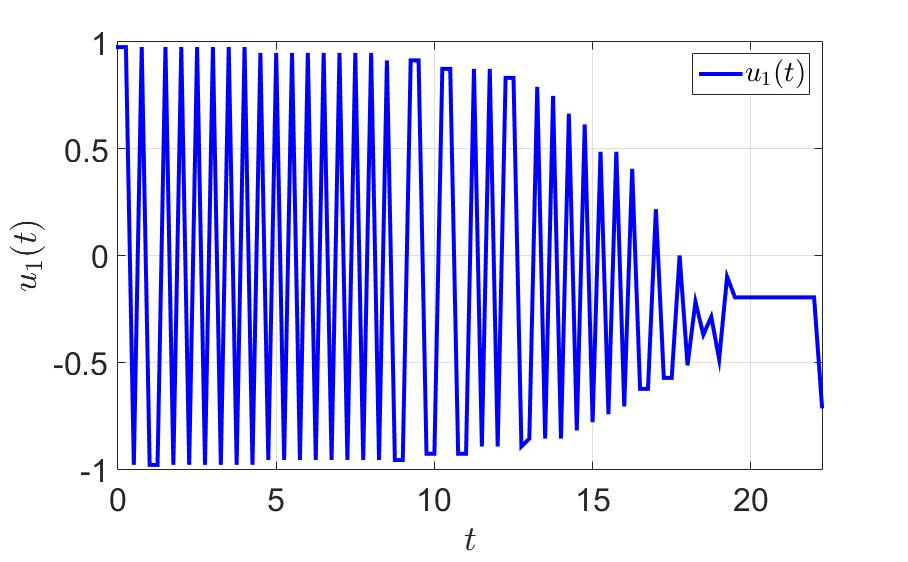
«ависимость первой компоненты управлени€ от времени.
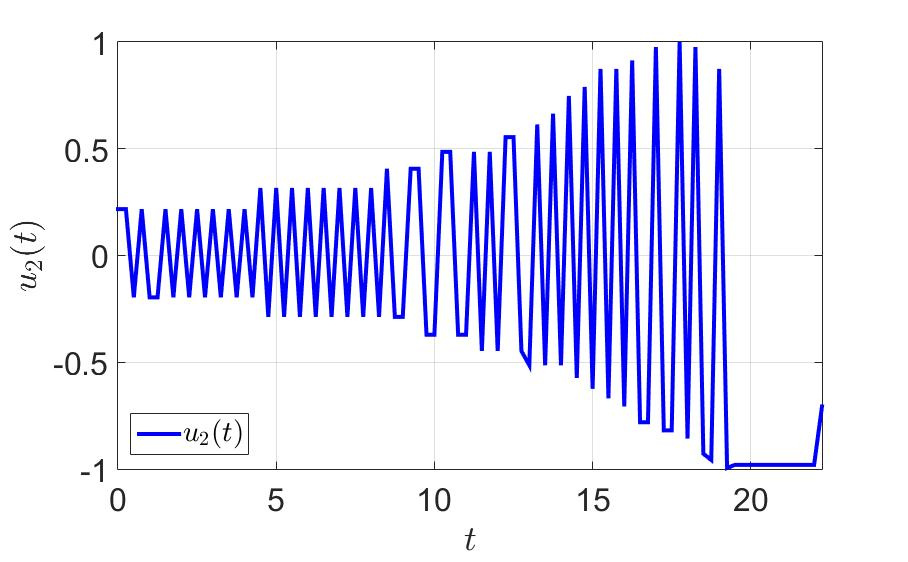
«ависимость второй компоненты управлени€ от времени.
¬ случае же использовани способа, обеспечивающего снижение количества переключений управлени€ врем€ успешного завершени€ игры первым игроком будет почти в трираза меньше:
$$display$$T = 8,80$$display$$
а соответствующие траектории показаны на следующих рисунках.
“раектори€ движени€ системы.
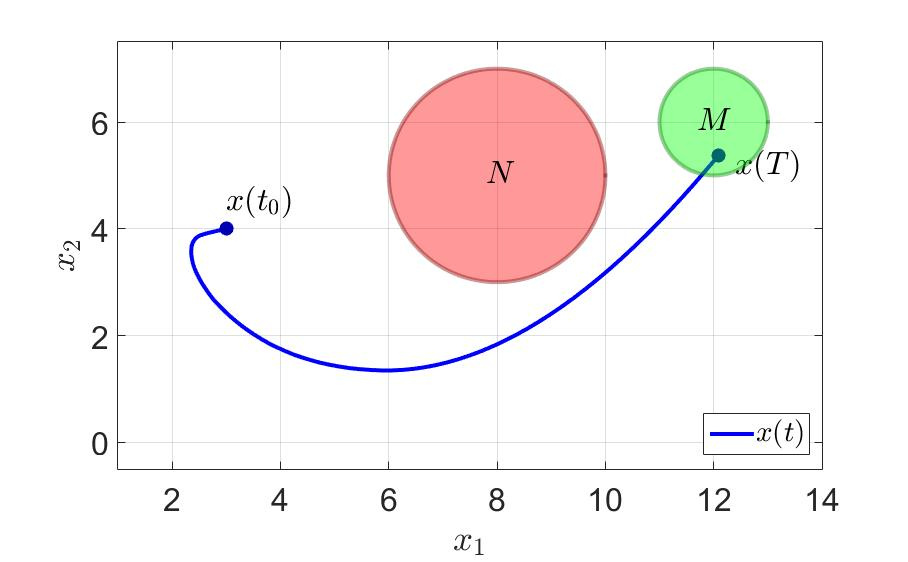
«ависимость первой компоненты управлени€ от времени.
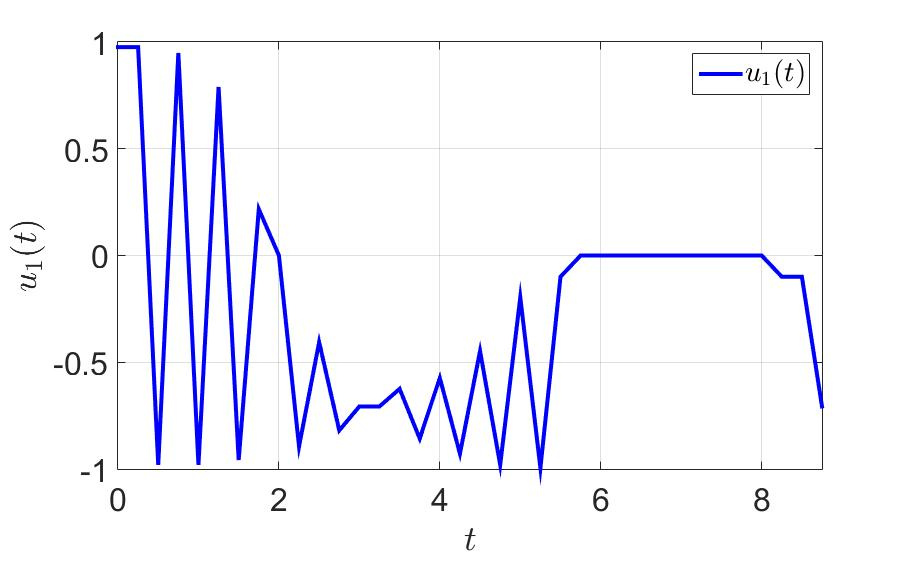
«ависимость второй компоненты управлени€ от времени.
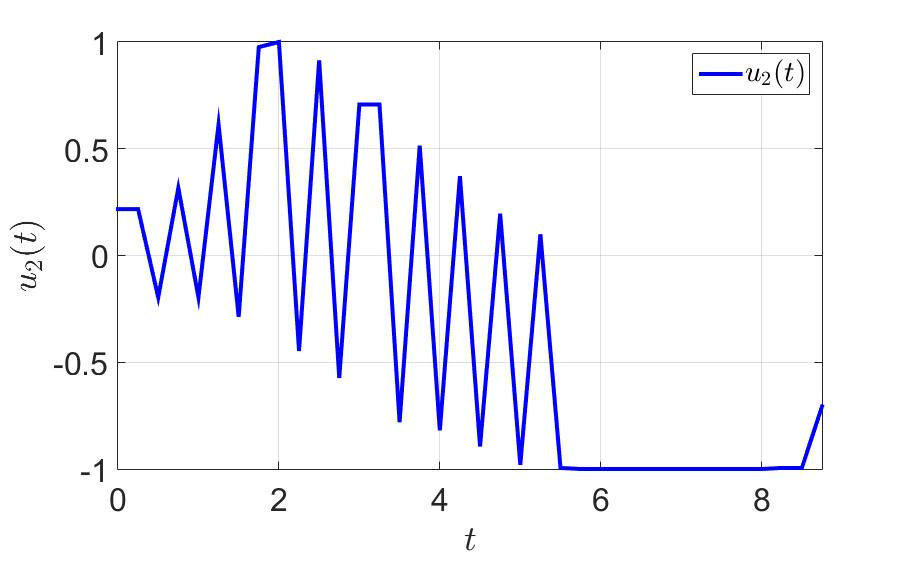
Ќа рисунках видно, что управление, полученное в ходе решени€ задачи описанным выше методом, обладает достаточно небольшим количеством переключений.
¬ыводы
„то в итоге получаем (если дочитали, конечно, до этого места), Ч "наивный" и "продвинутый" способы управлени€ динамической моделью, позвол€ющие конструктивно строить управление завис€щие исключительно от позиции (см. книги Ќ.Ќ. расовcкого, ј.». —убботина и Ћ.—. ѕонтр€гина), причем не облада€ полными знани€ми о помехе.
»сходники посмотреть можно здесь: репозитарий на GitHub
ѕредупреждаю сразу, что некоторым элементам кода уже пор€дка 19 лет, и они делались в то врем€, когда в C++ не было синтаксического сахара, да так и остались, т.к. работают. «а конструктивую критику будем признательны.
—ейчас, т.к. жизнь не может быть полностью описана линейными дифференциальными уравнени€ми, занимаемс€ нелинейными модел€ми, но там нет серебр€ной пули, т.е. "на пальцах" простое объ€снение дать не получитс€.
ќтдельное спасибо ≈катерине удешовой за критику.
Ѕибилиографи€
[1] ѕонтр€гин Ћ.—. ∆изнеописание Ћ. —. ѕонтр€гина, математика, составленное им самимї, ћ, 1983
[2] расовский Ќ.Ќ. “еори€ управлени€ движением: Ћинейные системы, ћ, Ќаука, 1968
[3] √ригоренко Ќ.Ћ. ћатематические методы управлени€ несколькими динамическими процессами, ћ, »здательство ћосковского ”ниверситета, 1990
[4] ё.Ќ. иселЄв, —.Ќ. јввакумов, ћ.¬. ќрлов ќѕ“»ћјЋ№Ќќ≈ ”ѕ–ј¬Ћ≈Ќ»≈. Ћ»Ќ≈…Ќјя “≈ќ–»я » ѕ–»Ћќ∆≈Ќ»я, ћ, 2007
[5] √ригоренко Ќ.Ћ., амзолкин ƒ.¬., ѕивоварчук ƒ.√. Ћинейные дифференциальные игры, ћ, 2007
[6] расовский Ќ.Ќ., —убботин ј.». ѕозиционные дифференциальные игры, ћ, Ќаука, 1974
[7] Ћи Ё.Ѕ., ћаркус Ћ. ќсновы теории оптимального управлени€, ћ, Ќаука, 1972
[8] ѕонтр€гин Ћ.—., Ѕолт€нский ¬.√., √амкрелидзе –.¬., ћищенко ≈.‘. ћатематическа€ теори€ оптимальных процессов, ћ, Ќаука, 1969
- определ€ем
| омментировать | « ѕред. запись — дневнику — —лед. запись » | —траницы: [1] [Ќовые] |






