[»з песочницы] вадратичное уравнение с комплексными числами в 3D |
¬сем привет! —о школы, реша€ квадратичные уравнени€ ( ” ), например , получал корни обладающие мнимой составл€ющей, , и при желании увидеть как график пересекает ось в точках , в интернете находил графики вроде:
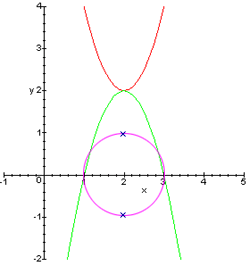
ак график с мнимой частью выгл€дит ( по моим размышлени€м ) в 3D (), и есть тема данной статьи.
PS: ѕод катом т€жЄлые анимации
„итать дальше →
ћетки:
author Sorbo
математика
метки: квадратное уравнение
комплексные числа
3d
графика

ак график с мнимой частью выгл€дит ( по моим размышлени€м ) в 3D (), и есть тема данной статьи.
PS: ѕод катом т€жЄлые анимации
„итать дальше →
https://habrahabr.ru/post/329672/?utm_source=habrahabr&utm_medium=rss&utm_campaign=best
| омментировать | « ѕред. запись — дневнику — —лед. запись » | —траницы: [1] [Ќовые] |






