ИНТЕГРАЦИЯ ДЕТЕРМИНИРОВАННЫХ ФРАКТАЛОВ И ХАОС |
ИНТЕГРАЦИЯ ДЕТЕРМИНИРОВАННЫХ ФРАКТАЛОВ И ХАОС
Из рассмотренных примеров детерминистских фракталов можно увидеть, что они не проявляют никакого хаотического поведения и что они на самом деле очень даже предсказуемы. Как известно, теория хаоса использует фрактал для того, чтобы воссоздать или найти закономерности с целью предсказания поведения многих систем в природе, таких как, например, проблема миграции птиц.
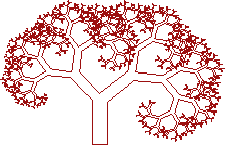
Теперь давайте посмотрим, как это в действительности происходит. Используя фрактал, называемый Деревом Пифагора, не рассматриваемого здесь (который, кстати, не изобретен Пифагором и никак не связан с теоремой Пифагора) и Броуновского движения (которое хаотично), давайте попытаемся сделать имитацию реального дерева. Упорядочение листьев и веток на дереве довольно сложно и случайно и, вероятно не является чем-то достаточно простым, что может эмулировать короткая программа из 12 строк.
Для начала нужно сгенерировать Дерево Пифагора (Рис. 6). Результат напоминает те старые детсадовские рисунки… Так что давайте сделаем ствол толще. На этой стадии Броуновское движение не используется. Вместо этого, каждый отрезок линии теперь стал линией симметрии прямоугольника, который становится стволом, и веток снаружи.
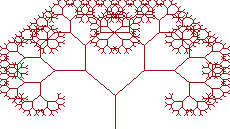
Но результат все еще выглядит слишком формальным и упорядоченным. Дерево еще не смотрится как живое. Попробуем применить некоторые из тех знаний в области детерминированных фракталов, которые мы только что приобрели.
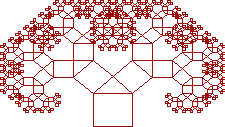
Теперь можно использовать Броуновское движение для создания некоторой случайной беспорядочности, которая изменяет числа, округляя их до двух разрядов. В оригинале были использованы 39 разрядные десятичные числа. Результат (Рис. 8) не выглядит как дерево. Вместо этого, он выглядит как хитроумный рыболовный крючок!
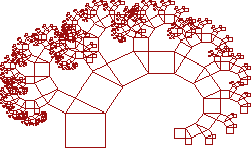
Может быть округление до 2 разрядов было слишком уж много? Снова применяем Броуновское движение, округленное на этот раз до 7 разрядов. Результат по-прежнему выглядит как рыболовный крючок, но на этот раз в форме логарифмической спирали (Рис. 9)
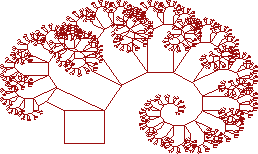
Так как левая сторона (содержащая все нечетные числа) не производит эффект крючка, случайные беспорядочности, произведенные Броуновским движением применяются дважды ко всем числам с левой стороны и только один раз к числам справа. Может быть этого будет достаточно чтобы исключить или уменьшить эффект логарифмической спирали. Итак, числа округляются до 24 разрядов. На этот раз, результат — приятно выглядящая компьютеризированная хаотическая эмуляция реального дерева (Рис. 10).
Из рассмотренных примеров детерминистских фракталов можно увидеть, что они не проявляют никакого хаотического поведения и что они на самом деле очень даже предсказуемы. Как известно, теория хаоса использует фрактал для того, чтобы воссоздать или найти закономерности с целью предсказания поведения многих систем в природе, таких как, например, проблема миграции птиц.
Теперь давайте посмотрим, как это в действительности происходит. Используя фрактал, называемый Деревом Пифагора, не рассматриваемого здесь (который, кстати, не изобретен Пифагором и никак не связан с теоремой Пифагора) и Броуновского движения (которое хаотично), давайте попытаемся сделать имитацию реального дерева. Упорядочение листьев и веток на дереве довольно сложно и случайно и, вероятно не является чем-то достаточно простым, что может эмулировать короткая программа из 12 строк.
Для начала нужно сгенерировать Дерево Пифагора (Рис. 6). Результат напоминает те старые детсадовские рисунки… Так что давайте сделаем ствол толще. На этой стадии Броуновское движение не используется. Вместо этого, каждый отрезок линии теперь стал линией симметрии прямоугольника, который становится стволом, и веток снаружи.

Но результат все еще выглядит слишком формальным и упорядоченным. Дерево еще не смотрится как живое. Попробуем применить некоторые из тех знаний в области детерминированных фракталов, которые мы только что приобрели.

Теперь можно использовать Броуновское движение для создания некоторой случайной беспорядочности, которая изменяет числа, округляя их до двух разрядов. В оригинале были использованы 39 разрядные десятичные числа. Результат (Рис. 8) не выглядит как дерево. Вместо этого, он выглядит как хитроумный рыболовный крючок!

Может быть округление до 2 разрядов было слишком уж много? Снова применяем Броуновское движение, округленное на этот раз до 7 разрядов. Результат по-прежнему выглядит как рыболовный крючок, но на этот раз в форме логарифмической спирали (Рис. 9)

Так как левая сторона (содержащая все нечетные числа) не производит эффект крючка, случайные беспорядочности, произведенные Броуновским движением применяются дважды ко всем числам с левой стороны и только один раз к числам справа. Может быть этого будет достаточно чтобы исключить или уменьшить эффект логарифмической спирали. Итак, числа округляются до 24 разрядов. На этот раз, результат — приятно выглядящая компьютеризированная хаотическая эмуляция реального дерева (Рис. 10).

|
|
ДВИЖЕНИЕ БИЛЛИАРДНОГО ШАРИКА |
ДВИЖЕНИЕ БИЛЛИАРДНОГО ШАРИКА
Любой, кто когда либо брал в руки кий для бильярда, знает, что ключ к игре — точность. Малейшая ошибка в угле начального удара может быстро привести к огромной ошибке в положении шарика всего после нескольких столкновений. Эта чувствительность к начальным условиям называемая хаосом возникает непреодолимым барьером для любого, кто надеется предсказать или управлять траекторией движения шарика больше чем после шести или семи столкновений. И не стоит думать, что проблема заключается в пыли на столе или в нетвердой руке. Фактически, если вы используете ваш компьютер для построения модели, содержащей бильярдный стол, не обладающий ни каким трением, нечеловеческим контролем точности позиционирования кия, вам все равно не удастся предсказывать траекторию шарика достаточно долго!

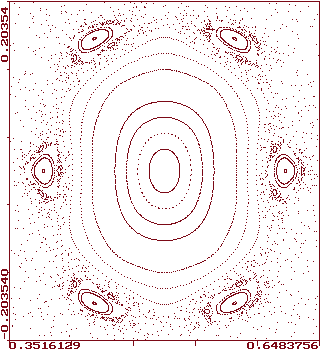
Насколько долго? Это зависит частично от точности вашего компьютера, но в большей степени от формы стола. Для совершенно круглого стола, можно просчитать приблизительно до 500 положений столкновений с ошибкой около 0.1 процента. Но стоит изменить форму стола так, чтобы она стала хотя бы немножко неправильной (овальной), и непредсказуемость траектории может превышать 90 градусов уже после 10 столкновений! Единственный путь получить картинку общего поведения бильярдного шарика, отскакивающего от чистого стола — это изобразить угол отскока или длину дуги соответствующую каждому удару. Здесь приведены два последовательных увеличения такой фазово-пространственной картины.
Каждая отдельная петля или область разброса точек представляет поведение шарика, происходящее от одного набора начальных условий. Область картинки, на которой отображаются результаты какого-то одного конкретного эксперимента, называется аттракторной областью для данного набора начальных условий. Как можно видеть форма стола, использованного для этих экспериментов является основной частью аттракторных областей, которые повторяются последовательно в уменьшающемся масштабе. Теоретически, такое самоподобие должно продолжаться вечно и если мы будем увеличивать рисунок все больше и больше, мы бы получали все те же формы. Это называется очень популярным сегодня словом фрактал
Любой, кто когда либо брал в руки кий для бильярда, знает, что ключ к игре — точность. Малейшая ошибка в угле начального удара может быстро привести к огромной ошибке в положении шарика всего после нескольких столкновений. Эта чувствительность к начальным условиям называемая хаосом возникает непреодолимым барьером для любого, кто надеется предсказать или управлять траекторией движения шарика больше чем после шести или семи столкновений. И не стоит думать, что проблема заключается в пыли на столе или в нетвердой руке. Фактически, если вы используете ваш компьютер для построения модели, содержащей бильярдный стол, не обладающий ни каким трением, нечеловеческим контролем точности позиционирования кия, вам все равно не удастся предсказывать траекторию шарика достаточно долго!


Насколько долго? Это зависит частично от точности вашего компьютера, но в большей степени от формы стола. Для совершенно круглого стола, можно просчитать приблизительно до 500 положений столкновений с ошибкой около 0.1 процента. Но стоит изменить форму стола так, чтобы она стала хотя бы немножко неправильной (овальной), и непредсказуемость траектории может превышать 90 градусов уже после 10 столкновений! Единственный путь получить картинку общего поведения бильярдного шарика, отскакивающего от чистого стола — это изобразить угол отскока или длину дуги соответствующую каждому удару. Здесь приведены два последовательных увеличения такой фазово-пространственной картины.
Каждая отдельная петля или область разброса точек представляет поведение шарика, происходящее от одного набора начальных условий. Область картинки, на которой отображаются результаты какого-то одного конкретного эксперимента, называется аттракторной областью для данного набора начальных условий. Как можно видеть форма стола, использованного для этих экспериментов является основной частью аттракторных областей, которые повторяются последовательно в уменьшающемся масштабе. Теоретически, такое самоподобие должно продолжаться вечно и если мы будем увеличивать рисунок все больше и больше, мы бы получали все те же формы. Это называется очень популярным сегодня словом фрактал
|
|
БРОУНОВСКОЕ ДВИЖЕНИЕ И ЕГО ПРИМЕНЕНИЯ |
БРОУНОВСКОЕ ДВИЖЕНИЕ И ЕГО ПРИМЕНЕНИЯ
Броуновское движение — это, например, случайное и хаотическое движение частичек пыли, взвешенных в воде. Этот тип движения, возможно, является аспектом фрактальной геометрии, имеющий с наибольшее практическое использование. Случайное Броуновское движение производит частотную диаграмму, которая может быть использована для предсказания вещей, включающих большие количества данных и статистики. Хорошим примером являются цены на шерсть, которые Мандельброт предсказал при помощи Броуновского движения.

Частотные диаграммы, созданные при построении графика на основе Броуновских чисел так же можно преобразовать в музыку. Конечно этот тип фрактальной музыки совсем не музыкален и может действительно утомить слушателя. Занося на график случайно Броуновские числа, можно получить Пылевой Фрактал наподобие того, что приведен здесь в качестве примера.
Кроме применения Броуновского движения для получения фракталов из фракталов, оно может использоваться и для создания ландшафтов. Во многих фантастических фильмах, как например Star Trek техника Броуновского движения была использована для создания инопланетных ландшафтов таких, как холмы и топологические картины высокогорных плато. Эти техники очень эффективны, и их можно найти в книге Мандельброта Фрактальная геометрия природы.
Мандельброт использовал Броуновские линии для создания фрактальных линий побережья и карт островов (которые на самом деле были просто в случайном порядке изображенные точки) с высоты птичьего полета.

Броуновское движение — это, например, случайное и хаотическое движение частичек пыли, взвешенных в воде. Этот тип движения, возможно, является аспектом фрактальной геометрии, имеющий с наибольшее практическое использование. Случайное Броуновское движение производит частотную диаграмму, которая может быть использована для предсказания вещей, включающих большие количества данных и статистики. Хорошим примером являются цены на шерсть, которые Мандельброт предсказал при помощи Броуновского движения.

Частотные диаграммы, созданные при построении графика на основе Броуновских чисел так же можно преобразовать в музыку. Конечно этот тип фрактальной музыки совсем не музыкален и может действительно утомить слушателя. Занося на график случайно Броуновские числа, можно получить Пылевой Фрактал наподобие того, что приведен здесь в качестве примера.
Кроме применения Броуновского движения для получения фракталов из фракталов, оно может использоваться и для создания ландшафтов. Во многих фантастических фильмах, как например Star Trek техника Броуновского движения была использована для создания инопланетных ландшафтов таких, как холмы и топологические картины высокогорных плато. Эти техники очень эффективны, и их можно найти в книге Мандельброта Фрактальная геометрия природы.
Мандельброт использовал Броуновские линии для создания фрактальных линий побережья и карт островов (которые на самом деле были просто в случайном порядке изображенные точки) с высоты птичьего полета.

|
|
ПРИМЕНЕНИЕ ТЕОРИИ ХАОСА В РЕАЛЬНОМ МИРЕ |
ПРИМЕНЕНИЕ ТЕОРИИ ХАОСА В РЕАЛЬНОМ МИРЕ
При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса?
Первое и самое важное — теория хаоса — это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание. Теория хаоса является очень хорошим средством взглянуть на события, происходящие в мире отлично от более традиционного четко детерминистического взгляда, который доминировал в науке со времен Ньютона. Зрители, которые посмотрели Парк Юрского периода, без сомнения боятся, что теория хаоса может очень сильно повлиять на человеческое восприятие мира, и, в действительности, теория хаоса полезна как средство интерпретации научных данных по-новому. Вместо традиционных X-Y графиков, ученые теперь могут интерпретировать фазово-пространственные диаграммы которые — вместо того, чтобы описывать точное положение какой-либо переменной в определенный момент времени — представляют общее поведение системы. Вместо того, чтобы смотреть на точные равенства, основанные на статистических данных, теперь мы можем взглянуть на динамические системы с поведением похожим по своей природе на статические данные — т.е. системы с похожими аттракторами. Теория хаоса обеспечивает прочный каркас для развития научных знаний.
Однако, согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.
Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.
В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.
Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.
И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.
При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса?
Первое и самое важное — теория хаоса — это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание. Теория хаоса является очень хорошим средством взглянуть на события, происходящие в мире отлично от более традиционного четко детерминистического взгляда, который доминировал в науке со времен Ньютона. Зрители, которые посмотрели Парк Юрского периода, без сомнения боятся, что теория хаоса может очень сильно повлиять на человеческое восприятие мира, и, в действительности, теория хаоса полезна как средство интерпретации научных данных по-новому. Вместо традиционных X-Y графиков, ученые теперь могут интерпретировать фазово-пространственные диаграммы которые — вместо того, чтобы описывать точное положение какой-либо переменной в определенный момент времени — представляют общее поведение системы. Вместо того, чтобы смотреть на точные равенства, основанные на статистических данных, теперь мы можем взглянуть на динамические системы с поведением похожим по своей природе на статические данные — т.е. системы с похожими аттракторами. Теория хаоса обеспечивает прочный каркас для развития научных знаний.
Однако, согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.
Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.
В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.
Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.
И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.
|
|
ЧТО ТАКОЕ ТЕОРИЯ ХАОСА? |
ЧТО ТАКОЕ ТЕОРИЯ ХАОСА?
Формально, теория хаоса определяется как учение о сложных нелинейных динамических системах. Под термином сложные это и понимается, а под термином нелинейные понимается рекурсия и алгоритмы из высшей математики, и, наконец, динамические — означает непостоянные и непериодические. Таким образом, теория хаоса - это учение о постоянно изменяющихся сложных системах, основанное не математических концепциях рекурсии, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему.
НЕПРАВИЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ ХАОСА
Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как Парк юрского периода, и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.
ТЕОРИЯ ХАОСА О БЕСПОРЯДКЕ
Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.
Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.
Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.

Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с колебаниями числа Авогадро (очень маленькое число порядка 1024), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии.
Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.к. он выражает общее поведение системы.
Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.
Формально, теория хаоса определяется как учение о сложных нелинейных динамических системах. Под термином сложные это и понимается, а под термином нелинейные понимается рекурсия и алгоритмы из высшей математики, и, наконец, динамические — означает непостоянные и непериодические. Таким образом, теория хаоса - это учение о постоянно изменяющихся сложных системах, основанное не математических концепциях рекурсии, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему.
НЕПРАВИЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ ХАОСА
Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как Парк юрского периода, и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.
ТЕОРИЯ ХАОСА О БЕСПОРЯДКЕ
Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.
Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.
Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.

Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с колебаниями числа Авогадро (очень маленькое число порядка 1024), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии.
Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.к. он выражает общее поведение системы.
Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.
|
|
Теория Хаоса |
ХАОСА ТЕОРИЯ, раздел математики, изучающий кажущееся случайным или очень сложное поведение детерминированных динамических систем. Динамическая система – это такая система, состояние которой меняется во времени в соответствии с фиксированными математическими правилами; последние обычно задаются уравнениями, связывающими будущее состояние системы с текущим. Такая система детерминирована, если эти правила не включают явным образом элемента случайности.
Вплоть до 1960-х годов многим казалось естественным полагать, что динамическая система, описываемая простыми детерминистическими уравнениями, должна вести себя относительно просто, хотя уже более столетия было известно, что это верно лишь в некоторых весьма специальных случаях, таких, как Солнечная система. Однако к 1980 математики и естествоиспытатели обнаружили, что хаос вездесущ.
Пример хаотического поведения из повседневной жизни – движение жидкости в миксере. Это устройство подчиняется простым механическим законам: его нож-смеситель вращается с постоянной скоростью, и взаимодействие жидкости с ножом внутри миксера можно описать простыми детерминистическими уравнениями. Однако возникающее при этом движение жидкости весьма сложно. Ее соседние области рассекаются ножом и разделяются, а отдаленные области могут сближаться. Короче говоря, жидкость перемешивается – для этого миксеры и предназначены.
Выражение «теория хаоса» используется преимущественно в популярной литературе. Специалисты же рассматривают эту дисциплину как раздел теории динамических систем.
Основные принципы. Для изучения хаоса используют общие математические принципы и компьютерное моделирование. Фундаментальной характеристикой всякой динамической системы является итерация, т.е. результат повторного (многократного) применения одного и того же математического правила к некоторому выбранному состоянию. Состояние обычно описывается числом или набором чисел, но это может быть также геометрическая фигура или конфигурация. Например, пусть правилом будет «разделить на два». Начав с исходного состояния, задаваемого числом 1, это правило дает итерации 1/2, 1/4, 1/8,..., образующие очевидную закономерную последовательность. Правило «возвести в квадрат и вычесть единицу», примененное к 0, дает последовательность –1, 0, –1, 0,..., которая циклически и неограниченно скачет между числами 0 и -1. Однако правило «возвести в квадрат, удвоить и затем вычесть единицу», если начать применять его, скажем, к значению 0,1, порождает последовательность чисел -0,98, 0,92, 0,69, -0,03,..., в которой не удается заметить никакой очевидной закономерности.
Основным понятием теории хаоса является аттрактор, т.е. то поведение, к которому в конце концов приходит или в пределе стремится система. Аттракторами для трех описанных выше систем являются: единственное число 0; пара чисел (0, -1); весь интервал чисел между –1 и 1. Динамика в этих трех случаях соответственно стационарная, периодическая и хаотическая. Хаотический аттрактор обладает скрытой структурой, которая часто становится явной после графического представления итераций. Состояние динамической системы – это набор чисел, которые можно интерпретировать как координаты изображающей его точки в некотором фазовом пространстве. Когда состояние системы меняется, эта точка движется. Для стационарного аттрактора движущаяся точка стремится к фиксированному положению, а для периодического аттрактора она циклически проходит через фиксированную последовательность положений. В случае хаотического аттрактора движущаяся точка образует более сложную конфигурацию с очень хитроумной, многослойной структурой. Такие конфигурации называют фракталами; этот термин был введен в 1970 Б.Мандельбротом. Его работы впоследствии стимулировали огромное количество исследований по фрактальной геометрии.
Важной чертой хаотической динамики является ее непредсказуемость. Представим себе две частички порошка, находящиеся рядом друг с другом в жидкости внутри миксера. После включения миксера эти две частички недолго останутся рядом; они быстро разойдутся в разные стороны и вскоре начнут двигаться независимо. Подобным же образом, если дважды запустить хаотическую систему из очень близких начальных состояний, ее поведение в этих двух случаях быстро станет совершенно непохожим. Это означает, что на больших временных интервалах хаотические системы непредсказуемы. Малейшая погрешность измерения начального состояния быстро растет, и предсказание будущего состояния становится все более неточным. Однако, в отличие от случайной системы, краткосрочное прогнозирование здесь возможно.
История вопроса. Понятие хаоса не было в явном виде сформулировано до 1960-х годов, но его истоки можно проследить начиная с последнего десятилетия 19 в., когда появилась удостоенная премии работа французского математика А.Пуанкаре о движении в Солнечной системе. Двумя столетиями раньше Ньютон установил закон всемирного тяготения, из которого вывел, что движение двух притягивающихся тел в отсутствие других сил описывается просто: каждое из них перемещается относительно их общего центра масс по одному из конических сечений – окружности, эллипсу, параболе, гиперболе или прямой. Для трех или большего числа тел, однако, нельзя найти подобного простого решения, и Пуанкаре показал, что эта трудность вызвана не недостатком человеческой изобретательности, а свойствами, внутренне присущими динамике многих тел. Он установил, что даже в ограниченной задаче трех тел, масса одного из которых пренебрежимо мала, возможно столь сложное движение, что его нельзя описать никакой математической формулой.
В 1926–1927 голландский инженер Б.Ван-дер-Пол сконструировал электронную схему, соответствующую математической модели сердечных сокращений. Он обнаружил, что при определенных условиях возникающие в схеме колебания были не периодическими, как при нормальном сердцебиении, а нерегулярными. Его работа получила серьезное математическое обоснование в годы Второй мировой войны, когда Дж.Литтлвуд и М.Картрайт исследовали принципы радиолокации. В начале 1960-х годов американский математик С.Смейл попытался построить исчерпывающую классификацию типичных разновидностей поведения динамических систем. Поначалу он предполагал, что можно обойтись различными комбинациями периодических движений, но вскоре понял, что возможно значительно более сложное поведение. В частности, он подробнее исследовал открытое Пуанкаре сложное движение в ограниченной задаче трех тел, упростив геометрию и получив при этом систему, известную ныне как «подкова Смейла». Он доказал, что такая система, несмотря на ее детерминированность, проявляет некоторые черты случайного поведения. Другие примеры подобных явлений были разработаны американской и российской школами в теории динамических систем, причем особенно важным оказался вклад В.И.Арнольда. Так начала возникать общая теория хаоса. Сам термин «хаос» ввели Дж.Йорке и Т.Ли в 1975 в краткой статье, посвященной обсуждению некоторых результатов исследований российской школы.
Исследования хаотических систем время от времени появлялись и в литературе по прикладным вопросам. Наиболее известная из таких моделей была введена метеорологом Э.Лоренцем в 1963. Лоренц построил модель конвекции в атмосфере, создав приближения очень сложных уравнений, описывающих это явление, значительно более простыми уравнениями с тремя неизвестными. Численно решая их на компьютере, он обнаружил, что решения колеблются нерегулярным, почти случайным образом. Лоренц также установил, что если слегка изменять начальные значения переменных, то отклонения будут усиливаться, пока новое решение не окажется совершенно непохожим на исходное. Описание им этого явления в последующих лекциях привело к популярному ныне выражению «эффект бабочки»: взмах крыла бабочки может изменить погоду.
Примеры приложений. Теория хаоса находит приложения в широком спектре наук. Одним из самых ранних стало ее применение к анализу турбулентности в жидкости. Движение жидкости бывает либо ламинарным (гладким и регулярным), либо турбулентным (сложным и нерегулярным). До появления теории хаоса существовали две конкурирующие теории турбулентности. Первая из них представляла турбулентность как накопление все новых и новых периодических движений; вторая объясняла неприменимость стандартной физической модели невозможностью описания жидкости как сплошной среды в молекулярных масштабах. В 1970 математики Д.Рюэль и Ф.Такенс предложили третью версию: турбулентность – это хаос в жидкости. Их предположение поначалу считалось весьма спорным, но с тех пор оно было подтверждено для нескольких случаев, в частности, для ранних стадий развития турбулентности в течении между двумя вращающимися цилиндрами. Развитая турбулентность по-прежнему остается загадочным явлением, но хаоса вряд ли удается избежать в любом возможном ее объяснении.
Ранняя работа Э.Лоренца в области метеорологии получила дальнейшее развитие, и теперь известно, что полные уравнения поведения атмосферы, используемые при прогнозировании погоды, могут вести себя хаотически. Это означает, что долгосрочные прогнозы погоды на основе данных о ее прошлом состоянии подвержены «эффекту бабочки», так что погода обычно не может быть предсказана более чем на четыре или пять дней вперед – независимо от мощности используемых компьютеров.
Движение в Солнечной системе тоже, как известно, хаотично, но здесь требуются десятки миллионов лет, прежде чем какое-то изменение станет непредсказуемым. Хаос проявляет себя многообразными способами. Например, спутник Сатурна Гиперион обращается по регулярной, предсказуемой орбите вокруг своей планеты, но при этом он хаотически кувыркается, изменяя направление оси собственного вращения. Теория хаоса объясняет это кувыркание как побочное действие приливных сил, создаваемых Сатурном. Теория хаоса объясняет также распределение тел в поясе астероидов между Марсом и Юпитером. Оно неравномерно: на одних расстояниях от Солнца существуют сгущения, на других – пустые промежутки. И сгущения, и пустые промежутки их гелиоцентрических орбит находятся на расстояниях, образующих «резонансы» с Юпитером, т.е. период обращения каждого астероида составляет некую простую дробь с периодом обращения Юпитера. Например, в резонансе 2:3 период обращения астероида равен 2/3 периода обращения Юпитера. Теория хаоса показывает, что одни резонансы порождают устойчивое поведение (сгущения), тогда как другие – неустойчивое (пустые промежутки). В частности, астероиды в резонансе 1:3 с Юпитером имеют неустойчивые орбиты и могут испытать возмущения, заставляющие их пересечь орбиту Марса, после чего они могут испытать дальнейшие возмущения и пересечь орбиту Земли. В 1995 Ж.Ласкар установил, что на временных масштабах десятков миллионов лет вся Солнечная система хаотична. Однако хаос не делает все черты движения в Солнечной системе непредсказуемыми. Например, форма планетной орбиты может быть предсказуемой, однако точное положение планеты на орбите остается непредсказуемым. Ласкар предсказал вероятное будущее Солнечной системы в целом на следующие несколько миллиардов лет. Согласно его вычислениям, ничего существенного не случится с орбитами внешних планет – Юпитера, Сатурна, Урана, Нептуна и Плутона. Орбиты Земли и Венеры тоже не претерпели бы существенных изменений, если бы не Марс, орбита которого изменится настолько, что он едва не столкнется с Землей. Меркурий тоже приблизится к Венере и будет либо выброшен из Солнечной системы, либо поменяется местами с Венерой.
Хаос имеет место также в биологии и экологии. В конце 19 в. было установлено, что популяции животных редко бывают стабильными; им свойственны нерегулярно чередующиеся периоды быстрого роста и почти полного вымирания. Теория хаоса показывает, что простые законы изменения численности популяций могут объяснить эти флуктуации без введения случайных внешних воздействий. Теория хаоса также объясняет динамику эпидемий, т.е. флуктуирующих популяций микроорганизмов в организмах людей.
Может создаться впечатление, что теория хаоса не должна иметь каких-либо полезных применений, поскольку хаотические системы непредсказуемы. Однако это неверно, во-первых, потому, что лишь некоторые аспекты хаотических систем непредсказуемы, и, во-вторых, потому, что полезность теории не ограничивается способностью прямого прогнозирования. В частности, теория хаоса предлагает новые методы анализа данных и обнаружения скрытых закономерностей там, где прежде систему считали случайной и никаких закономерностей в ее поведении не искали, полагая, что их просто не существует. Одним из приложений этого подхода служит машина FRACMAT, обеспечивающая дешевую и быструю процедуру контроля качества пружинной проволоки.
К числу наиболее перспективных применений теории хаоса принадлежит «хаотическое управление». В 1950 Дж.фон Нейман предположил, что неустойчивость погоды может в один прекрасный день обернуться благом, поскольку неустойчивость означает, что желаемый эффект может быть достигнут очень малым возмущением. В 1990 С.Гребоджи, Э.Отт и Дж.Йорке опубликовали теоретическую схему использования этого вида неустойчивости для управления хаотическими системами. Их схема представляет собой общую форму того метода, с помощью которого в 1985 инженеры НАСА послали космический зонд на встречу с кометой Джакобини – Циннера. Зонд пять раз облетел Луну, используя хаотичность взаимодействия трех тел, позволяющую совершать большие изменения траектории с малыми затратами топлива. Тот же метод был применен для синхронизации батареи лазеров; для управления нерегулярностями сердцебиения, что открывает возможность создать «интеллектуальный» стимулятор сердечного ритма; для управления биотоками мозга, что, в частности, может помочь контролировать эпилептические припадки; наконец, для ламинаризации турбулентного течения жидкости – метод, который способен уменьшить расход топлива самолетами.
Вплоть до 1960-х годов многим казалось естественным полагать, что динамическая система, описываемая простыми детерминистическими уравнениями, должна вести себя относительно просто, хотя уже более столетия было известно, что это верно лишь в некоторых весьма специальных случаях, таких, как Солнечная система. Однако к 1980 математики и естествоиспытатели обнаружили, что хаос вездесущ.
Пример хаотического поведения из повседневной жизни – движение жидкости в миксере. Это устройство подчиняется простым механическим законам: его нож-смеситель вращается с постоянной скоростью, и взаимодействие жидкости с ножом внутри миксера можно описать простыми детерминистическими уравнениями. Однако возникающее при этом движение жидкости весьма сложно. Ее соседние области рассекаются ножом и разделяются, а отдаленные области могут сближаться. Короче говоря, жидкость перемешивается – для этого миксеры и предназначены.
Выражение «теория хаоса» используется преимущественно в популярной литературе. Специалисты же рассматривают эту дисциплину как раздел теории динамических систем.
Основные принципы. Для изучения хаоса используют общие математические принципы и компьютерное моделирование. Фундаментальной характеристикой всякой динамической системы является итерация, т.е. результат повторного (многократного) применения одного и того же математического правила к некоторому выбранному состоянию. Состояние обычно описывается числом или набором чисел, но это может быть также геометрическая фигура или конфигурация. Например, пусть правилом будет «разделить на два». Начав с исходного состояния, задаваемого числом 1, это правило дает итерации 1/2, 1/4, 1/8,..., образующие очевидную закономерную последовательность. Правило «возвести в квадрат и вычесть единицу», примененное к 0, дает последовательность –1, 0, –1, 0,..., которая циклически и неограниченно скачет между числами 0 и -1. Однако правило «возвести в квадрат, удвоить и затем вычесть единицу», если начать применять его, скажем, к значению 0,1, порождает последовательность чисел -0,98, 0,92, 0,69, -0,03,..., в которой не удается заметить никакой очевидной закономерности.
Основным понятием теории хаоса является аттрактор, т.е. то поведение, к которому в конце концов приходит или в пределе стремится система. Аттракторами для трех описанных выше систем являются: единственное число 0; пара чисел (0, -1); весь интервал чисел между –1 и 1. Динамика в этих трех случаях соответственно стационарная, периодическая и хаотическая. Хаотический аттрактор обладает скрытой структурой, которая часто становится явной после графического представления итераций. Состояние динамической системы – это набор чисел, которые можно интерпретировать как координаты изображающей его точки в некотором фазовом пространстве. Когда состояние системы меняется, эта точка движется. Для стационарного аттрактора движущаяся точка стремится к фиксированному положению, а для периодического аттрактора она циклически проходит через фиксированную последовательность положений. В случае хаотического аттрактора движущаяся точка образует более сложную конфигурацию с очень хитроумной, многослойной структурой. Такие конфигурации называют фракталами; этот термин был введен в 1970 Б.Мандельбротом. Его работы впоследствии стимулировали огромное количество исследований по фрактальной геометрии.
Важной чертой хаотической динамики является ее непредсказуемость. Представим себе две частички порошка, находящиеся рядом друг с другом в жидкости внутри миксера. После включения миксера эти две частички недолго останутся рядом; они быстро разойдутся в разные стороны и вскоре начнут двигаться независимо. Подобным же образом, если дважды запустить хаотическую систему из очень близких начальных состояний, ее поведение в этих двух случаях быстро станет совершенно непохожим. Это означает, что на больших временных интервалах хаотические системы непредсказуемы. Малейшая погрешность измерения начального состояния быстро растет, и предсказание будущего состояния становится все более неточным. Однако, в отличие от случайной системы, краткосрочное прогнозирование здесь возможно.
История вопроса. Понятие хаоса не было в явном виде сформулировано до 1960-х годов, но его истоки можно проследить начиная с последнего десятилетия 19 в., когда появилась удостоенная премии работа французского математика А.Пуанкаре о движении в Солнечной системе. Двумя столетиями раньше Ньютон установил закон всемирного тяготения, из которого вывел, что движение двух притягивающихся тел в отсутствие других сил описывается просто: каждое из них перемещается относительно их общего центра масс по одному из конических сечений – окружности, эллипсу, параболе, гиперболе или прямой. Для трех или большего числа тел, однако, нельзя найти подобного простого решения, и Пуанкаре показал, что эта трудность вызвана не недостатком человеческой изобретательности, а свойствами, внутренне присущими динамике многих тел. Он установил, что даже в ограниченной задаче трех тел, масса одного из которых пренебрежимо мала, возможно столь сложное движение, что его нельзя описать никакой математической формулой.
В 1926–1927 голландский инженер Б.Ван-дер-Пол сконструировал электронную схему, соответствующую математической модели сердечных сокращений. Он обнаружил, что при определенных условиях возникающие в схеме колебания были не периодическими, как при нормальном сердцебиении, а нерегулярными. Его работа получила серьезное математическое обоснование в годы Второй мировой войны, когда Дж.Литтлвуд и М.Картрайт исследовали принципы радиолокации. В начале 1960-х годов американский математик С.Смейл попытался построить исчерпывающую классификацию типичных разновидностей поведения динамических систем. Поначалу он предполагал, что можно обойтись различными комбинациями периодических движений, но вскоре понял, что возможно значительно более сложное поведение. В частности, он подробнее исследовал открытое Пуанкаре сложное движение в ограниченной задаче трех тел, упростив геометрию и получив при этом систему, известную ныне как «подкова Смейла». Он доказал, что такая система, несмотря на ее детерминированность, проявляет некоторые черты случайного поведения. Другие примеры подобных явлений были разработаны американской и российской школами в теории динамических систем, причем особенно важным оказался вклад В.И.Арнольда. Так начала возникать общая теория хаоса. Сам термин «хаос» ввели Дж.Йорке и Т.Ли в 1975 в краткой статье, посвященной обсуждению некоторых результатов исследований российской школы.
Исследования хаотических систем время от времени появлялись и в литературе по прикладным вопросам. Наиболее известная из таких моделей была введена метеорологом Э.Лоренцем в 1963. Лоренц построил модель конвекции в атмосфере, создав приближения очень сложных уравнений, описывающих это явление, значительно более простыми уравнениями с тремя неизвестными. Численно решая их на компьютере, он обнаружил, что решения колеблются нерегулярным, почти случайным образом. Лоренц также установил, что если слегка изменять начальные значения переменных, то отклонения будут усиливаться, пока новое решение не окажется совершенно непохожим на исходное. Описание им этого явления в последующих лекциях привело к популярному ныне выражению «эффект бабочки»: взмах крыла бабочки может изменить погоду.
Примеры приложений. Теория хаоса находит приложения в широком спектре наук. Одним из самых ранних стало ее применение к анализу турбулентности в жидкости. Движение жидкости бывает либо ламинарным (гладким и регулярным), либо турбулентным (сложным и нерегулярным). До появления теории хаоса существовали две конкурирующие теории турбулентности. Первая из них представляла турбулентность как накопление все новых и новых периодических движений; вторая объясняла неприменимость стандартной физической модели невозможностью описания жидкости как сплошной среды в молекулярных масштабах. В 1970 математики Д.Рюэль и Ф.Такенс предложили третью версию: турбулентность – это хаос в жидкости. Их предположение поначалу считалось весьма спорным, но с тех пор оно было подтверждено для нескольких случаев, в частности, для ранних стадий развития турбулентности в течении между двумя вращающимися цилиндрами. Развитая турбулентность по-прежнему остается загадочным явлением, но хаоса вряд ли удается избежать в любом возможном ее объяснении.
Ранняя работа Э.Лоренца в области метеорологии получила дальнейшее развитие, и теперь известно, что полные уравнения поведения атмосферы, используемые при прогнозировании погоды, могут вести себя хаотически. Это означает, что долгосрочные прогнозы погоды на основе данных о ее прошлом состоянии подвержены «эффекту бабочки», так что погода обычно не может быть предсказана более чем на четыре или пять дней вперед – независимо от мощности используемых компьютеров.
Движение в Солнечной системе тоже, как известно, хаотично, но здесь требуются десятки миллионов лет, прежде чем какое-то изменение станет непредсказуемым. Хаос проявляет себя многообразными способами. Например, спутник Сатурна Гиперион обращается по регулярной, предсказуемой орбите вокруг своей планеты, но при этом он хаотически кувыркается, изменяя направление оси собственного вращения. Теория хаоса объясняет это кувыркание как побочное действие приливных сил, создаваемых Сатурном. Теория хаоса объясняет также распределение тел в поясе астероидов между Марсом и Юпитером. Оно неравномерно: на одних расстояниях от Солнца существуют сгущения, на других – пустые промежутки. И сгущения, и пустые промежутки их гелиоцентрических орбит находятся на расстояниях, образующих «резонансы» с Юпитером, т.е. период обращения каждого астероида составляет некую простую дробь с периодом обращения Юпитера. Например, в резонансе 2:3 период обращения астероида равен 2/3 периода обращения Юпитера. Теория хаоса показывает, что одни резонансы порождают устойчивое поведение (сгущения), тогда как другие – неустойчивое (пустые промежутки). В частности, астероиды в резонансе 1:3 с Юпитером имеют неустойчивые орбиты и могут испытать возмущения, заставляющие их пересечь орбиту Марса, после чего они могут испытать дальнейшие возмущения и пересечь орбиту Земли. В 1995 Ж.Ласкар установил, что на временных масштабах десятков миллионов лет вся Солнечная система хаотична. Однако хаос не делает все черты движения в Солнечной системе непредсказуемыми. Например, форма планетной орбиты может быть предсказуемой, однако точное положение планеты на орбите остается непредсказуемым. Ласкар предсказал вероятное будущее Солнечной системы в целом на следующие несколько миллиардов лет. Согласно его вычислениям, ничего существенного не случится с орбитами внешних планет – Юпитера, Сатурна, Урана, Нептуна и Плутона. Орбиты Земли и Венеры тоже не претерпели бы существенных изменений, если бы не Марс, орбита которого изменится настолько, что он едва не столкнется с Землей. Меркурий тоже приблизится к Венере и будет либо выброшен из Солнечной системы, либо поменяется местами с Венерой.
Хаос имеет место также в биологии и экологии. В конце 19 в. было установлено, что популяции животных редко бывают стабильными; им свойственны нерегулярно чередующиеся периоды быстрого роста и почти полного вымирания. Теория хаоса показывает, что простые законы изменения численности популяций могут объяснить эти флуктуации без введения случайных внешних воздействий. Теория хаоса также объясняет динамику эпидемий, т.е. флуктуирующих популяций микроорганизмов в организмах людей.
Может создаться впечатление, что теория хаоса не должна иметь каких-либо полезных применений, поскольку хаотические системы непредсказуемы. Однако это неверно, во-первых, потому, что лишь некоторые аспекты хаотических систем непредсказуемы, и, во-вторых, потому, что полезность теории не ограничивается способностью прямого прогнозирования. В частности, теория хаоса предлагает новые методы анализа данных и обнаружения скрытых закономерностей там, где прежде систему считали случайной и никаких закономерностей в ее поведении не искали, полагая, что их просто не существует. Одним из приложений этого подхода служит машина FRACMAT, обеспечивающая дешевую и быструю процедуру контроля качества пружинной проволоки.
К числу наиболее перспективных применений теории хаоса принадлежит «хаотическое управление». В 1950 Дж.фон Нейман предположил, что неустойчивость погоды может в один прекрасный день обернуться благом, поскольку неустойчивость означает, что желаемый эффект может быть достигнут очень малым возмущением. В 1990 С.Гребоджи, Э.Отт и Дж.Йорке опубликовали теоретическую схему использования этого вида неустойчивости для управления хаотическими системами. Их схема представляет собой общую форму того метода, с помощью которого в 1985 инженеры НАСА послали космический зонд на встречу с кометой Джакобини – Циннера. Зонд пять раз облетел Луну, используя хаотичность взаимодействия трех тел, позволяющую совершать большие изменения траектории с малыми затратами топлива. Тот же метод был применен для синхронизации батареи лазеров; для управления нерегулярностями сердцебиения, что открывает возможность создать «интеллектуальный» стимулятор сердечного ритма; для управления биотоками мозга, что, в частности, может помочь контролировать эпилептические припадки; наконец, для ламинаризации турбулентного течения жидкости – метод, который способен уменьшить расход топлива самолетами.
|
|
теория хаоса |
Теория хаоса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных, при определённых условиях, явлению, известному как хаос, которое характеризуется сильной чувствительностью поведения системы к начальным условиям. Результатом такой чувствительности является то, что поведение такой системы кажется случайным, даже если модель, описывающая систему является детерминированной. Примерами подобных систем являются атмосфера, турбулентные потоки, биологические популяции, общество как система коммуникаций и его подсистемы: экономические, политические и другие социальные системы.
Математические системы с хаотическим поведением являются детерминированными, то есть подчиняются некоторому строгому закону и, в каком-то смысле, являются упорядоченными. Такое использование слова «хаос», отличается от его обычного значения (см. хаос в мифологии). Существует, также, такая область физики, как теория квантового хаоса, изучающая недетерминированные системы, подчиняющиеся законам квантовой механики.
Математические системы с хаотическим поведением являются детерминированными, то есть подчиняются некоторому строгому закону и, в каком-то смысле, являются упорядоченными. Такое использование слова «хаос», отличается от его обычного значения (см. хаос в мифологии). Существует, также, такая область физики, как теория квантового хаоса, изучающая недетерминированные системы, подчиняющиеся законам квантовой механики.
|
|
Эффект бабочки |
Даже такая мелочь как взмах крыла бабочки может привести к тайфуну на другом конце планеты.
(Эффект бабочки, Теория Хаоса)

(Эффект бабочки, Теория Хаоса)

|
|
Рэй Бредбери. И грянул Гром |
И грянул гром
Объявление на стене расплылось, словно его затянуло пленкой скользящей теплой воды; Экельс почувствовал, как веки, смыкаясь, на долю секунды прикрыли зрачки, но и в мгновенном мраке горели буквы:
А/О САФАРИ ВО ВРЕМЕНИ
ОРГАНИЗУЕМ САФАРИ В ЛЮБОЙ ГОД ПРОШЛОГО
ВЫ ВЫБИРАЕТЕ ДОБЫЧУ
МЫ ДОСТАВЛЯЕМ ВАС НА МЕСТО
ВЫ УБИВАЕТЕ ЕЕ
В глотке Экельса скопилась теплая слизь; он судорожно глотнул. Мускулы вокруг рта растянули губы в улыбку, когда он медленно поднял руку, в которой покачивался чек на десять тысяч долларов, предназначенный для человека за конторкой.
- Вы гарантируете, что я вернусь из сафари живым?
- Мы ничего не гарантируем, - ответил служащий, - кроме динозавров. - Он повернулся. - Вот мистер Тревис, он будет вашим проводником в Прошлое. Он скажет вам, где и когда стрелять. Если скажет "не стрелять", значит - не стрелять. Не выполните его распоряжения, по возвращении заплатите штраф - еще десять тысяч, кроме того, ждите неприятностей от правительства.
В дальнем конце огромного помещения конторы Экельс видел нечто причудливое и неопределенное, извивающееся и гудящее, переплетение проводов и стальных кожухов, переливающийся яркий ореол - то оранжевый, то серебристый, то голубой. Гул был такой, словно само Время горело на могучем костре, словно все годы, все даты летописей, все дни свалили в одну кучу и подожгли.
Одно прикосновение руки - и тотчас это горение послушно даст задний ход. Экельс помнил каждое слово объявления. Из пепла и праха, из пыли и золы восстанут, будто золотистые саламандры, старые годы, зеленые годы, розы усладят воздух, седые волосы станут черными, исчезнут морщины и складки, все и вся повернет вспять и станет семенем, от смерти ринется к своему истоку, солнца будут всходить на западе и погружаться в зарево востока, луны будут убывать с другого конца, все и вся уподобится цыпленку, прячущемуся в яйцо, кроликам, ныряющим в шляпу фокусника, все и вся познает новую смерть, смерть семени, зеленую смерть, возвращения в пору, предшествующую зачатию. И это будет сделано одним лишь движением руки...
- Черт возьми, - выдохнул Экельс; на его худом лице мелькали блики света от Машины - Настоящая Машина времени! - Он покачал головой. - Подумать только. Закончись выборы вчера иначе, и я сегодня, быть может, пришел бы сюда спасаться бегством. Слава богу, что победил Кейт. В Соединенных Штатах будет хороший президент.
- Вот именно, - отозвался человек за конторкой. - Нам повезло. Если бы выбрали Дойчера, не миновать нам жесточайшей диктатуры. Этот тип против всего на свете - против мира, против веры, против человечности, против разума. Люди звонили нам и справлялись - шутя, конечно, а впрочем... Дескать, если Дойчер будет президентом, нельзя ли перебраться в 1492 год. Да только не наше это дело - побеги устраивать. Мы организуем сафари. Так или иначе, Кейт - президент, и у вас теперь одна забота...
- ...убить моего динозавра, - закончил фразу Экельс.
- Tyrannosaurus rex. Громогласный Ящер, отвратительнейшее чудовище в истории планеты. Подпишите вот это. Что бы с вами ни произошло, мы не отвечаем. У этих динозавров зверский аппетит.
Экельс вспыхнул от возмущения.
- Вы пытаетесь испугать меня?
- По чести говоря, да. Мы вовсе не желаем отправлять в прошлое таких, что при первом же выстреле ударяются в панику. В том году погибло шесть руководителей и дюжина охотников. Мы предоставляем вам случай испытать самое чертовское приключение, о каком только может мечтать настоящий охотник. Путешествие на шестьдесят миллионов лет назад и величайшая добыча всех времен! Вот ваш чек. Порвите его.
Мистер Экельс долго, смотрел на чек. Пальцы его дрожали.
- Ни пуха, ни пера, - сказал человек за конторкой. - Мистер Тревис, займитесь клиентом.
Неся ружья в руках, они молча прошли через комнату к Машине, к серебристому металлу и рокочущему свету.
Сперва день, затем ночь, опять день, опять ночь; потом день - ночь, день - ночь, день. Неделя, месяц, год, десятилетие! 2055 год. 2019, 1999! 1957! Мимо! Машина ревела.
Они надели кислородные шлемы, проверили наушники.
Экельс качался на мягком сиденье - бледный, зубы стиснуты Он ощутил судорожную дрожь в руках, посмотрел вниз и увидел, как его пальцы сжали новое ружье. В машине было еще четверо. Тревис - руководитель сафари, его помощник Лесперанс и два охотника - Биллингс и Кремер. Они сидели, глядя друг на друга, а мимо, точно вспышки молний, проносились годы.
- Это ружье может убить динозавра? - вымолвили губы Экельса.
- Если верно попадешь, - ответил в наушниках Тревис. - У некоторых динозавров два мозга: один в голове, другой ниже по позвоночнику. Таких мы не трогаем. Лучше не злоупотреблять своей счастливой звездой. Первые две пули в глаза, если сумеете, конечно. Ослепили, тогда бейте в мозг.
Машина взвыла. Время было словно кинолента, пущенная обратным ходом. Солнца летели вспять, за ними мчались десятки миллионов лун.
- Господи, - произнес Экельс. - Все охотники, когда-либо жившие на свете, позавидовали бы нам сегодня. Тут тебе сама Африка покажется Иллинойсом.
Машина замедлила ход, вой сменился ровным гулом. Машина остановилась.
Солнце остановилось на небе.
Мгла, окружавшая Машину, рассеялась, они были в древности, глубокой-глубокой древности, три охотника и два руководителя, у каждого на коленях ружье - голубой вороненый ствол.
- Христос еще не родился, - сказал Тревис. - Моисей не ходил еще на гору беседовать с богом. Пирамиды лежат в земле, камни для них еще не обтесаны и не сложены. Помните об этом. Александр, Цезарь, Наполеон, Гитлер - никого из них нет.
Они кивнули.
- Вот, - мистер Тревис указал пальцем, - вот джунгли за шестьдесят миллионов две тысячи пятьдесят пять лет до президента Кейта.
Он показал на металлическую тропу, которая через распаренное болото уходила в зеленые заросли, извиваясь между огромными папоротниками и пальмами.
- А это, - объяснил он, - Тропа, проложенная здесь для охотников Компанией. Она парит над землей на высоте шести дюймов. Не задевает ни одного дерева, ни одного цветка, ни одной травинки. Сделана из антигравитационного металла. Ее назначение - изолировать вас от этого мира прошлого, чтобы вы ничего не коснулись. Держитесь Тропы. Не сходите с нее. Повторяю: не сходите с нее. Ни при каких обстоятельствах! Если свалитесь с нее - штраф. И не стреляйте ничего без нашего разрешения.
- Почему? - спросил Экельс.
Они сидели среди древних зарослей. Ветер нес далекие крики птиц, нес запах смолы и древнего соленого моря, запах влажной травы и кроваво-красных цветов.
- Мы не хотим изменять Будущее. Здесь, в Прошлом, мы незваные гости. Правительство не одобряет наши экскурсии. Приходится платить немалые взятки, чтобы нас не лишили концессии Машина времени - дело щекотливое. Сами того не зная, мы можем убить какое-нибудь важное животное, пичугу, жука, раздавить цветок и уничтожить важное звено в развитии вида.
- Я что-то не понимаю, - сказал Экельс.
- Ну так слушайте, - продолжал Тревис. - Допустим, мы случайно убили здесь мышь. Это значит, что всех будущих потомков этой мыши уже не будет - верно?
- Да.
- Не будет потомков от потомков от всех ее потомков! Значит, неосторожно ступив ногой, вы уничтожаете не одну, и не десяток, и не тысячу, а миллион - миллиард мышей!
- Хорошо, они сдохли, - согласился Экельс. - Ну и что?
- Что? - Тревис презрительно фыркнул. - А как с лисами, для питания которых нужны были именно эти мыши? Не хватит десяти мышей - умрет одна лиса. Десятью лисами меньше - подохнет от голода лев. Одним львом меньше - погибнут всевозможные насекомые и стервятники, сгинет неисчислимое множество форм жизни. И вот итог: через пятьдесят девять миллионов лет пещерный человек, один из дюжины, населяющей весь мир, гонимый голодом, выходит на охоту за кабаном или саблезубым тигром. Но вы, друг мой, раздавив одну мышь, тем самым раздавили всех тигров в этих местах. И пещерный человек умирает от голода. А этот человек, заметьте себе, не просто один человек, нет! Это целый будущий народ. Из его чресел вышло бы десять сыновей. От них произошло бы сто - и так далее, и возникла бы целая цивилизация. Уничтожьте одного человека - и вы уничтожите целое племя, народ, историческую эпоху. Это все равно что убить одного из внуков Адама. Раздавите ногой мышь - это будет равносильно землетрясению, которое исказит облик всей земли, в корне изменит наши судьбы. Гибель одного пещерного человека - смерть миллиарда его потомков, задушенных во чреве. Может быть, Рим не появится на своих семи холмах. Европа навсегда останется глухим лесом, только в Азии расцветет пышная жизнь. Наступите на мышь - и вы сокрушите пирамиды. Наступите на мышь - и вы оставите на Вечности вмятину величиной с Великий Каньон. Не будет королевы Елизаветы, Вашингтон не перейдет Делавер. Соединенные Штаты вообще не появятся. Так что будьте осторожны. Держитесь тропы. Никогда не сходите с нее!
- Понимаю, - сказал Экельс. - Но тогда, выходит, опасно касаться даже травы?
- Совершенно верно. Нельзя предсказать, к чему приведет гибель того или иного растения. Малейшее отклонение сейчас неизмеримо возрастет за шестьдесят миллионов лет. Разумеется, не исключено, что наша теория ошибочна. Быть может, мы не в состоянии повлиять на Время. А если и в состоянии - то очень незначительно. Скажем, мертвая мышь ведет к небольшому отклонению в мире насекомых, дальше - к угнетению вида, еще дальше - к неурожаю, депрессии, голоду, наконец, к изменениям социальным. А может быть, итог будет совсем незаметным - легкое дуновение, шепот, волосок, пылинка в воздухе, такое, что сразу не увидишь. Кто знает? Кто возьмется предугадать? Мы не знаем - только гадаем. И покуда нам не известно совершенно точно, что наши вылазки во Времени для истории - гром или легкий шорох, надо быть чертовски осторожным. Эта Машина, эта Тропа, ваша одежда, вы сами, как вам известно, - все обеззаражено. И назначение этих кислородных шлемов - помешать нам внести в древний воздух наши бактерии.
- Но откуда мы знаем, каких зверей убивать?
- Они помечены красной краской, - ответил Тревис. - Сегодня, перед нашей отправкой, мы послали сюда на Машине Лесперанса. Он побывал как раз в этом времени и проследил за некоторыми животными.
- Изучал их?
- Вот именно, - отозвался Лесперанс. - Я прослеживаю всю их жизнь и отмечаю, какие особи живут долго. Таких очень мало. Сколько раз они спариваются. Редко... Жизнь коротка. Найдя зверя, которого подстерегает смерть под упавшим деревом или в асфальтовом озере, я отмечаю час, минуту, секунду, когда он гибнет. Затем стреляю красящей пулей. Она оставляет на коже красную метку. Когда экспедиция отбывает в Прошлое, я рассчитываю все так, чтобы мы явились минуты за две до того, как животное все равно погибнет. Так что мы убиваем только те особи, у которых нет будущего, которым и без того уже не спариться. Видите, насколько мы осторожны?
- Но если вы утром побывали здесь, - взволнованно заговорил Экельс, - то должны были встретить нас, нашу экспедицию! Как она прошла? Успешно? Все остались живы?
Тревис и Лесперанс переглянулись.
- Это был бы парадокс, - сказал Лесперанс. - Такой путаницы, чтобы человек встретил самого себя, Время не допускает. Если возникает такая опасность. Время делает шаг в сторону. Вроде того, как самолет проваливается в воздушную яму. Вы заметили, как Машину тряхнуло перед самой нашей остановкой? Это мы миновали самих себя по пути обратно в Будущее. Но мы не видели ничего. Поэтому невозможно сказать, удалась ли наша экспедиция, уложили ли мы зверя, вернулись ли мы - вернее, вы, мистер Экельс, - обратно живые.
Экельс бледно улыбнулся.
- Ну, все, - отрезал Тревис. - Встали!
Пора было выходить из Машины.
Джунгли были высокие, и джунгли были широкие, и джунгли были навеки всем миром. Воздух наполняли звуки, словно музыка, словно паруса бились в воздухе - это летели, будто исполинские летучие мыши из кошмара, из бреда, махая огромными, как пещерный свод, серыми крыльями, птеродактили. Экельс, стоя на узкой Тропе, шутя прицелился.
- Эй, бросьте! - скомандовал Тревис. - Даже в шутку не цельтесь, черт бы вас побрал! Вдруг выстрелит...
Экельс покраснел.
- Где же наш Tyrannosaurus rex?
Лесперанс взглянул на свои часы.
- На подходе. Мы встретимся ровно через шестьдесят секунд. И ради бога - не прозевайте красное пятно. Пока не скажем, не стрелять. И не сходите с Тропы. Не сходите с тропы!
Они шли навстречу утреннему ветерку.
- Странно, - пробормотал Экельс. - Перед нами - шестьдесят миллионов лет. Выборы прошли. Кейт стал президентом. Все празднуют победу. А мы - здесь, все эти миллионы лет словно ветром сдуло, их нет. Всего того, что заботило нас на протяжении нашей жизни, еще нет и в помине, даже в проекте.
- Приготовиться! - скомандовал Тревис. - Первый выстрел ваш, Экельс. Биллингс - второй номер. За ним - Кремер.
- Я охотился на тигров, кабанов, буйволов, слонов, но видит бог - это совсем другое дело, - произнес Экельс. - Я дрожу, как мальчишка.
- Тихо, - сказал Тревис.
Все остановились.
Тревис поднял руку.
- Впереди, - прошептал он. - В тумане. Он там. Встречайте Его Королевское Величество.
Безбрежные джунгли были полны щебета, шороха, бормотанья, вздохов.
Вдруг все смолкло, точно кто-то затворил дверь.
Тишина.
Раскат грома.
Из мглы ярдах в ста впереди появился Tyrannosaurus rex.
- Силы небесные, - пролепетал Экельс.
- Тсс!
Оно шло на огромных, лоснящихся, пружинящих, мягко ступающих ногах.
Оно за тридцать футов возвышалось над лесом - великий бог зла, прижавший хрупкие руки часовщика к маслянистой груди рептилии. Ноги - могучие поршни, тысяча фунтов белой кости, оплетенные тугими каналами мышц под блестящей морщинистой кожей, подобной кольчуге грозного воина. Каждое бедро - тонна мяса, слоновой кости и кольчужной стали. А из громадной вздымающейся грудной клетки торчали две тонкие руки, руки с пальцами, которые могли подобрать и исследовать человека, будто игрушку. Извивающаяся змеиная шея легко вздымала к небу тысячекилограммовый каменный монолит головы. Разверстая пасть обнажала частокол зубов-кинжалов. Вращались глаза - страусовые яйца, не выражая ничего, кроме голода. Оно сомкнуло челюсти в зловещем оскале. Оно побежало, и задние ноги смяли кусты и деревья, и когти вспороли сырую землю, оставляя следы шестидюймовой глубины. Оно бежало скользящим балетным шагом, неправдоподобно уверенно и легко для десятитонной махины. Оно настороженно вышло на залитую солнцем прогалину и пощупало воздух своими красивыми чешуйчатыми руками.
- Господи! - Губы Экельса дрожали. - Да оно, если вытянется, луну достать может.
- Тсс! - сердито зашипел Тревис. - Он еще не заметил нас.
- Его нельзя убить. - Экельс произнес это спокойно, словно заранее отметал все возражения. Он взвесил показания очевидцев и вынес окончательное решение. Ружье в его руках было словно пугач. - Идиоты, и что нас сюда принесло... Это же невозможно.
- Молчать! - рявкнул Тревис.
- Кошмар...
- Кру-гом! - скомандовал Тревис. - Спокойно возвращайтесь в Машину. Половина суммы будет вам возвращена.
- Я не ждал, что оно окажется таким огромным, - сказал Экельс. - Одним словом, просчитался. Нет, я участвовать не буду.
- Оно заметило нас!
- Вон красное пятно на груди!
Громогласный Ящер выпрямился. Его бронированная плоть сверкала, словно тысяча зеленых монет. Монеты покрывала жаркая слизь. В слизи копошились мелкие козявки, и все тело переливалось, будто по нему пробегали волны, даже когда чудовище стояло неподвижно. Оно глухо дохнуло. Над поляной повис запах сырого мяса.
- Помогите мне уйти, - сказал Экельс. - Раньше все было иначе. Я всегда знал, что останусь жив. Были надежные проводники, удачные сафари, никакой опасности. На сей раз я просчитался. Это мне не по силам. Признаюсь. Орешек мне не по зубам.
- Не бегите, - сказал Лесперанс. - Повернитесь кругом. Спрячьтесь в Машине.
- Да. - Казалось, Экельс окаменел. Он поглядел на свои ноги, словно пытался заставить их двигаться. Он застонал от бессилия.
- Экельс!
Он сделал шаг - другой, зажмурившись, волоча ноги.
- Не в ту сторону!
Едва он двинулся с места, как чудовище с ужасающим воем ринулось вперед. Сто ярдов оно покрыло за четыре секунды. Ружья взметнулись вверх и дали залп. Из пасти зверя вырвался ураган, обдав людей запахом слизи и крови. Чудовище взревело, его зубы сверкали на солнце.
Не оглядываясь, Экельс слепо шагнул к краю Тропы, сошел с нее и, сам того не сознавая, направился в джунгли; ружье бесполезно болталось в руках. Ступни тонули в зеленом мху, ноги влекли его прочь, он чувствовал себя одиноким и далеким от того, что происходило за его спиной.
Снова затрещали ружья. Выстрелы потонули в громовом реве ящера. Могучий хвост рептилии дернулся, точно кончик бича, и деревья взорвались облаками листьев и веток. Чудовище протянуло вниз свои руки ювелира - погладить людей, разорвать их пополам, раздавить, как ягоды, и сунуть в пасть, в ревущую глотку! Глыбы глаз очутились возле людей. Они увидели свое отражение. Они открыли огонь по металлическим векам и пылающим черным зрачкам.
Словно каменный идол, словно горный обвал, рухнул. Tyrannosaurus rex.
Рыча, он цеплялся за деревья и валил их. Зацепил и смял металлическую Тропу. Люди бросились назад, отступая. Десять тонн холодного мяса, как утес, грохнулись оземь. Ружья дали еще залп. Чудовище ударило бронированным хвостом, щелкнуло змеиными челюстями и затихло. Из горла фонтаном била кровь. Где-то внутри лопнул бурдюк с жидкостью, и зловонный поток захлестнул охотников. Они стояли неподвижно, облитые чем-то блестящим, красным.
Гром смолк.
В джунглях воцарилась тишина. После обвала - зеленый покой. После кошмара - утро.
Биллингс и Кремер сидели на Тропе; им было плохо. Тревис и Лесперанс стояли рядом, держа дымящиеся ружья и чертыхаясь.
Экельс, весь дрожа, лежал ничком в Машине Времени. Каким-то образом он выбрался обратно на Тропу и добрел до Машины.
Подошел Тревис, глянул на Экельса, достал из ящика марлю и вернулся к тем, что сидели на Тропе.
- Оботритесь.
Они стерли со шлемов кровь. И тоже принялись чертыхаться. Чудовище лежало неподвижно. Гора мяса, из недр которой доносилось бульканье, вздохи - это умирали клетки, органы переставали действовать, и соки последний раз текли по своим ходам, все отключалось, навсегда выходя из строя. Точно вы стояли возле разбитого паровоза или закончившего рабочий день парового катка - все клапаны открыты или плотно зажаты. Затрещали кости: вес мышц, ничем не управляемый - мертвый вес, - раздавил тонкие руки, притиснутые к земле. Колыхаясь, оно приняло покойное положение.
Вдруг снова грохот. Высоко над ними сломался исполинский сук. С гулом он обрушился на безжизненное чудовище, как бы окончательно утверждая его гибель.
- Так. - Лесперанс поглядел на часы. - Минута в минуту. Это тот самый сук, который должен был его убить. - Он обратился к двум охотникам. - Фотография трофея вам нужна?
- Что?
- Мы не можем увозить добычу в Будущее. Туша должна лежать здесь, на своем месте, чтобы ею могли питаться насекомые, птицы, бактерии. Равновесие нарушать нельзя. Поэтому добычу оставляют. Но мы можем сфотографировать вас возле нее.
Охотники сделали над собой усилие, пытаясь думать, но сдались, тряся головой.
Они послушно дали отвести себя в Машину. Устало опустились на сиденья. Тупо оглянулись на поверженное чудовище - немой курган. На остывающей броне уже копошились золотистые насекомые, сидели причудливые птицеящеры.
Внезапный шум заставил охотников оцепенеть: на полу Машины, дрожа, сидел Экельс.
- Простите меня, - сказал он.
- Встаньте! - рявкнул Тревис.
Экельс встал.
- Ступайте на Тропу, - скомандовал Тревис. Он поднял ружье. - Вы не вернетесь с Машиной. Вы останетесь здесь!
Лесперанс перехватил руку Тревиса.
- Постой...
- А ты не суйся! - Тревис стряхнул его руку. - Из-за этого подонка мы все чуть не погибли. Но главное даже не это. Нет, черт возьми, ты погляди на его башмаки! Гляди! Он соскочил с Тропы. Понимаешь, чем это нам грозит? Один бог знает, какой штраф нам прилепят! Десятки тысяч долларов! Мы гарантируем, что никто не сойдет с Тропы. Он сошел. Идиот чертов! Я обязан доложить правительству. И нас могут лишить концессии на эти сафари. А какие последствия будут для Времени, для Истории?!
- Успокойся, он набрал на подошвы немного грязи - только и всего.
- Откуда мы можем знать? - крикнул Тревис. - Мы ничего не знаем! Это же все сплошная загадка! Шагом марш, Экельс!
Экельс полез в карман.
- Я заплачу сколько угодно. Сто тысяч долларов! Тревис покосился на чековую книжку и плюнул.
- Ступайте! Чудовище лежит возле Тропы. Суньте ему руки по локоть в пасть. Потом можете вернуться к нам.
- Это несправедливо!
- Зверь мертв, ублюдок несчастный. Пули! Пули не должны оставаться здесь, в Прошлом. Они могут повлиять на развитие. Вот вам нож. Вырежьте их!
Джунгли опять пробудились к жизни и наполнились древними шорохами, птичьими голосами. Экельс медленно повернулся и остановил взгляд на доисторической падали, глыбе кошмаров и ужасов. Наконец, словно лунатик, побрел по Тропе.
Пять минут спустя он, дрожа всем телом, вернулся к Машине, его руки были по локоть красны от крови.
Он протянул вперед обе ладони. На них блестели стальные пули. Потом он упал. Он лежал там, где упал недвижимый.
- Напрасно ты его заставил это делать, - сказал Лесперанс.
- Напрасно! Об этом рано судить. - Тревис толкнул неподвижное тело. - Не помрет. Больше его не потянет за такой добычей. А теперь, - он сделал вялый жест рукой, - включай. Двигаемся домой.
1492. 1776. 1812
Они умыли лицо и руки. Они сняли заскорузлые от крови рубахи, брюки и надели все чистое. Экельс пришел в себя, но сидел молча. Тревис добрых десять минут в упор смотрел на него.
- Не глядите на меня, - вырвалось у Экельса. - Я ничего не сделал.
- Кто знает.
- Я только соскочил с Тропы и вымазал башмаки глиной. Чего вы от меня хотите? Чтобы я вас на коленях умолял?
- Это не исключено. Предупреждаю Вас, Экельс, может еще случиться, что я вас убью. Ружье заряжено.
- Я не виноват. Я ничего не сделал.
1999. 2000. 2055.
Машина остановилась.
- Выходите, - скомандовал Тревис.
Комната была такая же, как прежде. Хотя нет, не совсем такая же. Тот же человек сидел за той же конторкой. Нет, не совсем тот же человек, и конторка не та же.
Тревис быстро обвел помещение взглядом.
- Все в порядке? - буркнул он.
- Конечно. С благополучным возвращением!
Но настороженность не покидала Тревиса. Казалось, он проверяет каждый атом воздуха, придирчиво исследует свет солнца, падающий из высокого окна.
- О'кей, Экельс, выходите. И больше никогда не попадайтесь мне на глаза.
Экельс будто окаменел.
- Ну? - поторопил его Тревис. - Что вы там такое увидели?
Экельс медленно вдыхал воздух - с воздухом что-то произошло, какое-то химическое изменение, настолько незначительное, неуловимое, что лишь слабый голос подсознания говорил Экельсу о перемене. И краски - белая, серая, синяя, оранжевая, на стенах, мебели, в небе за окном - они... они... да: что с ними случилось? А тут еще это ощущение. По коже бегали мурашки. Руки дергались. Всеми порами тела он улавливал нечто странное, чужеродное. Будто где-то кто-то свистнул в свисток, который слышат только собаки. И его тело беззвучно откликнулось. За окном, за стенами этого помещения, за спиной человека (который был не тем человеком) у перегородки (которая была не той перегородкой) - целый мир улиц и людей. Но как отсюда определить, что это за мир теперь, что за люди? Он буквально чувствовал, как они движутся там, за стенами, - словно шахматные фигурки, влекомые сухим ветром...
Зато сразу бросалось в глаза объявление на стене, объявление, которое он уже читал сегодня, когда впервые вошел сюда.
Что-то в нем было не так.
А/О СОФАРИ ВОВРЕМЕНИ
АРГАНИЗУЕМ СОФАРИ ВЛЮБОЙ ГОД ПРОШЛОГО
ВЫ ВЫБЕРАЕТЕ ДАБЫЧУ
МЫ ДАСТАВЛЯЕМ ВАС НАМЕСТО
ВЫ УБЕВАЕТЕ ЕЕ
Экельс почувствовал, что опускается на стул. Он стал лихорадочно скрести грязь на башмаках. Его дрожащая рука подняла липкий ком.
- Нет, не может быть! Из-за такой малости... Нет!
На комке было отливающее зеленью, золотом и чернью пятно - бабочка, очень красивая... мертвая.
- Из-за такой малости! Из-за бабочки! - закричал Экельс.
Она упала на пол - изящное маленькое создание, способное нарушить равновесие, повалились маленькие костяшки домино... большие костяшки... огромные костяшки, соединенные цепью неисчислимых лет, составляющих Время. Мысли Экельса смещались. Не может быть, чтобы она что-то изменила. Мертвая бабочка - и такие последствия? Невозможно!
Его лицо похолодело Непослушными губами он вымолвил:
- Кто... кто вчера победил на выборах?
Человек за конторкой хихикнул.
- Шутите? Будто не знаете! Дойчер, разумеется! Кто же еще? Уж не этот ли хлюпик Кейт? Теперь у власти железный человек! - Служащий опешил. - Что это с вами?
Экельс застонал. Он упал на колени. Дрожащие пальцы протянулись к золотистой бабочке.
- Неужели нельзя, - молил он весь мир, себя, служащего, Машину, - вернуть ее туда, оживить ее? Неужели нельзя начать все сначала? Может быть...
Он лежал неподвижно. Лежал, закрыв глаза, дрожа, и ждал. Он отчетливо слышал тяжелое дыхание Тревиса, слышал, как Тревис поднимает ружье и нажимает курок.
И грянул гром.
1952
Объявление на стене расплылось, словно его затянуло пленкой скользящей теплой воды; Экельс почувствовал, как веки, смыкаясь, на долю секунды прикрыли зрачки, но и в мгновенном мраке горели буквы:
А/О САФАРИ ВО ВРЕМЕНИ
ОРГАНИЗУЕМ САФАРИ В ЛЮБОЙ ГОД ПРОШЛОГО
ВЫ ВЫБИРАЕТЕ ДОБЫЧУ
МЫ ДОСТАВЛЯЕМ ВАС НА МЕСТО
ВЫ УБИВАЕТЕ ЕЕ
В глотке Экельса скопилась теплая слизь; он судорожно глотнул. Мускулы вокруг рта растянули губы в улыбку, когда он медленно поднял руку, в которой покачивался чек на десять тысяч долларов, предназначенный для человека за конторкой.
- Вы гарантируете, что я вернусь из сафари живым?
- Мы ничего не гарантируем, - ответил служащий, - кроме динозавров. - Он повернулся. - Вот мистер Тревис, он будет вашим проводником в Прошлое. Он скажет вам, где и когда стрелять. Если скажет "не стрелять", значит - не стрелять. Не выполните его распоряжения, по возвращении заплатите штраф - еще десять тысяч, кроме того, ждите неприятностей от правительства.
В дальнем конце огромного помещения конторы Экельс видел нечто причудливое и неопределенное, извивающееся и гудящее, переплетение проводов и стальных кожухов, переливающийся яркий ореол - то оранжевый, то серебристый, то голубой. Гул был такой, словно само Время горело на могучем костре, словно все годы, все даты летописей, все дни свалили в одну кучу и подожгли.
Одно прикосновение руки - и тотчас это горение послушно даст задний ход. Экельс помнил каждое слово объявления. Из пепла и праха, из пыли и золы восстанут, будто золотистые саламандры, старые годы, зеленые годы, розы усладят воздух, седые волосы станут черными, исчезнут морщины и складки, все и вся повернет вспять и станет семенем, от смерти ринется к своему истоку, солнца будут всходить на западе и погружаться в зарево востока, луны будут убывать с другого конца, все и вся уподобится цыпленку, прячущемуся в яйцо, кроликам, ныряющим в шляпу фокусника, все и вся познает новую смерть, смерть семени, зеленую смерть, возвращения в пору, предшествующую зачатию. И это будет сделано одним лишь движением руки...
- Черт возьми, - выдохнул Экельс; на его худом лице мелькали блики света от Машины - Настоящая Машина времени! - Он покачал головой. - Подумать только. Закончись выборы вчера иначе, и я сегодня, быть может, пришел бы сюда спасаться бегством. Слава богу, что победил Кейт. В Соединенных Штатах будет хороший президент.
- Вот именно, - отозвался человек за конторкой. - Нам повезло. Если бы выбрали Дойчера, не миновать нам жесточайшей диктатуры. Этот тип против всего на свете - против мира, против веры, против человечности, против разума. Люди звонили нам и справлялись - шутя, конечно, а впрочем... Дескать, если Дойчер будет президентом, нельзя ли перебраться в 1492 год. Да только не наше это дело - побеги устраивать. Мы организуем сафари. Так или иначе, Кейт - президент, и у вас теперь одна забота...
- ...убить моего динозавра, - закончил фразу Экельс.
- Tyrannosaurus rex. Громогласный Ящер, отвратительнейшее чудовище в истории планеты. Подпишите вот это. Что бы с вами ни произошло, мы не отвечаем. У этих динозавров зверский аппетит.
Экельс вспыхнул от возмущения.
- Вы пытаетесь испугать меня?
- По чести говоря, да. Мы вовсе не желаем отправлять в прошлое таких, что при первом же выстреле ударяются в панику. В том году погибло шесть руководителей и дюжина охотников. Мы предоставляем вам случай испытать самое чертовское приключение, о каком только может мечтать настоящий охотник. Путешествие на шестьдесят миллионов лет назад и величайшая добыча всех времен! Вот ваш чек. Порвите его.
Мистер Экельс долго, смотрел на чек. Пальцы его дрожали.
- Ни пуха, ни пера, - сказал человек за конторкой. - Мистер Тревис, займитесь клиентом.
Неся ружья в руках, они молча прошли через комнату к Машине, к серебристому металлу и рокочущему свету.
Сперва день, затем ночь, опять день, опять ночь; потом день - ночь, день - ночь, день. Неделя, месяц, год, десятилетие! 2055 год. 2019, 1999! 1957! Мимо! Машина ревела.
Они надели кислородные шлемы, проверили наушники.
Экельс качался на мягком сиденье - бледный, зубы стиснуты Он ощутил судорожную дрожь в руках, посмотрел вниз и увидел, как его пальцы сжали новое ружье. В машине было еще четверо. Тревис - руководитель сафари, его помощник Лесперанс и два охотника - Биллингс и Кремер. Они сидели, глядя друг на друга, а мимо, точно вспышки молний, проносились годы.
- Это ружье может убить динозавра? - вымолвили губы Экельса.
- Если верно попадешь, - ответил в наушниках Тревис. - У некоторых динозавров два мозга: один в голове, другой ниже по позвоночнику. Таких мы не трогаем. Лучше не злоупотреблять своей счастливой звездой. Первые две пули в глаза, если сумеете, конечно. Ослепили, тогда бейте в мозг.
Машина взвыла. Время было словно кинолента, пущенная обратным ходом. Солнца летели вспять, за ними мчались десятки миллионов лун.
- Господи, - произнес Экельс. - Все охотники, когда-либо жившие на свете, позавидовали бы нам сегодня. Тут тебе сама Африка покажется Иллинойсом.
Машина замедлила ход, вой сменился ровным гулом. Машина остановилась.
Солнце остановилось на небе.
Мгла, окружавшая Машину, рассеялась, они были в древности, глубокой-глубокой древности, три охотника и два руководителя, у каждого на коленях ружье - голубой вороненый ствол.
- Христос еще не родился, - сказал Тревис. - Моисей не ходил еще на гору беседовать с богом. Пирамиды лежат в земле, камни для них еще не обтесаны и не сложены. Помните об этом. Александр, Цезарь, Наполеон, Гитлер - никого из них нет.
Они кивнули.
- Вот, - мистер Тревис указал пальцем, - вот джунгли за шестьдесят миллионов две тысячи пятьдесят пять лет до президента Кейта.
Он показал на металлическую тропу, которая через распаренное болото уходила в зеленые заросли, извиваясь между огромными папоротниками и пальмами.
- А это, - объяснил он, - Тропа, проложенная здесь для охотников Компанией. Она парит над землей на высоте шести дюймов. Не задевает ни одного дерева, ни одного цветка, ни одной травинки. Сделана из антигравитационного металла. Ее назначение - изолировать вас от этого мира прошлого, чтобы вы ничего не коснулись. Держитесь Тропы. Не сходите с нее. Повторяю: не сходите с нее. Ни при каких обстоятельствах! Если свалитесь с нее - штраф. И не стреляйте ничего без нашего разрешения.
- Почему? - спросил Экельс.
Они сидели среди древних зарослей. Ветер нес далекие крики птиц, нес запах смолы и древнего соленого моря, запах влажной травы и кроваво-красных цветов.
- Мы не хотим изменять Будущее. Здесь, в Прошлом, мы незваные гости. Правительство не одобряет наши экскурсии. Приходится платить немалые взятки, чтобы нас не лишили концессии Машина времени - дело щекотливое. Сами того не зная, мы можем убить какое-нибудь важное животное, пичугу, жука, раздавить цветок и уничтожить важное звено в развитии вида.
- Я что-то не понимаю, - сказал Экельс.
- Ну так слушайте, - продолжал Тревис. - Допустим, мы случайно убили здесь мышь. Это значит, что всех будущих потомков этой мыши уже не будет - верно?
- Да.
- Не будет потомков от потомков от всех ее потомков! Значит, неосторожно ступив ногой, вы уничтожаете не одну, и не десяток, и не тысячу, а миллион - миллиард мышей!
- Хорошо, они сдохли, - согласился Экельс. - Ну и что?
- Что? - Тревис презрительно фыркнул. - А как с лисами, для питания которых нужны были именно эти мыши? Не хватит десяти мышей - умрет одна лиса. Десятью лисами меньше - подохнет от голода лев. Одним львом меньше - погибнут всевозможные насекомые и стервятники, сгинет неисчислимое множество форм жизни. И вот итог: через пятьдесят девять миллионов лет пещерный человек, один из дюжины, населяющей весь мир, гонимый голодом, выходит на охоту за кабаном или саблезубым тигром. Но вы, друг мой, раздавив одну мышь, тем самым раздавили всех тигров в этих местах. И пещерный человек умирает от голода. А этот человек, заметьте себе, не просто один человек, нет! Это целый будущий народ. Из его чресел вышло бы десять сыновей. От них произошло бы сто - и так далее, и возникла бы целая цивилизация. Уничтожьте одного человека - и вы уничтожите целое племя, народ, историческую эпоху. Это все равно что убить одного из внуков Адама. Раздавите ногой мышь - это будет равносильно землетрясению, которое исказит облик всей земли, в корне изменит наши судьбы. Гибель одного пещерного человека - смерть миллиарда его потомков, задушенных во чреве. Может быть, Рим не появится на своих семи холмах. Европа навсегда останется глухим лесом, только в Азии расцветет пышная жизнь. Наступите на мышь - и вы сокрушите пирамиды. Наступите на мышь - и вы оставите на Вечности вмятину величиной с Великий Каньон. Не будет королевы Елизаветы, Вашингтон не перейдет Делавер. Соединенные Штаты вообще не появятся. Так что будьте осторожны. Держитесь тропы. Никогда не сходите с нее!
- Понимаю, - сказал Экельс. - Но тогда, выходит, опасно касаться даже травы?
- Совершенно верно. Нельзя предсказать, к чему приведет гибель того или иного растения. Малейшее отклонение сейчас неизмеримо возрастет за шестьдесят миллионов лет. Разумеется, не исключено, что наша теория ошибочна. Быть может, мы не в состоянии повлиять на Время. А если и в состоянии - то очень незначительно. Скажем, мертвая мышь ведет к небольшому отклонению в мире насекомых, дальше - к угнетению вида, еще дальше - к неурожаю, депрессии, голоду, наконец, к изменениям социальным. А может быть, итог будет совсем незаметным - легкое дуновение, шепот, волосок, пылинка в воздухе, такое, что сразу не увидишь. Кто знает? Кто возьмется предугадать? Мы не знаем - только гадаем. И покуда нам не известно совершенно точно, что наши вылазки во Времени для истории - гром или легкий шорох, надо быть чертовски осторожным. Эта Машина, эта Тропа, ваша одежда, вы сами, как вам известно, - все обеззаражено. И назначение этих кислородных шлемов - помешать нам внести в древний воздух наши бактерии.
- Но откуда мы знаем, каких зверей убивать?
- Они помечены красной краской, - ответил Тревис. - Сегодня, перед нашей отправкой, мы послали сюда на Машине Лесперанса. Он побывал как раз в этом времени и проследил за некоторыми животными.
- Изучал их?
- Вот именно, - отозвался Лесперанс. - Я прослеживаю всю их жизнь и отмечаю, какие особи живут долго. Таких очень мало. Сколько раз они спариваются. Редко... Жизнь коротка. Найдя зверя, которого подстерегает смерть под упавшим деревом или в асфальтовом озере, я отмечаю час, минуту, секунду, когда он гибнет. Затем стреляю красящей пулей. Она оставляет на коже красную метку. Когда экспедиция отбывает в Прошлое, я рассчитываю все так, чтобы мы явились минуты за две до того, как животное все равно погибнет. Так что мы убиваем только те особи, у которых нет будущего, которым и без того уже не спариться. Видите, насколько мы осторожны?
- Но если вы утром побывали здесь, - взволнованно заговорил Экельс, - то должны были встретить нас, нашу экспедицию! Как она прошла? Успешно? Все остались живы?
Тревис и Лесперанс переглянулись.
- Это был бы парадокс, - сказал Лесперанс. - Такой путаницы, чтобы человек встретил самого себя, Время не допускает. Если возникает такая опасность. Время делает шаг в сторону. Вроде того, как самолет проваливается в воздушную яму. Вы заметили, как Машину тряхнуло перед самой нашей остановкой? Это мы миновали самих себя по пути обратно в Будущее. Но мы не видели ничего. Поэтому невозможно сказать, удалась ли наша экспедиция, уложили ли мы зверя, вернулись ли мы - вернее, вы, мистер Экельс, - обратно живые.
Экельс бледно улыбнулся.
- Ну, все, - отрезал Тревис. - Встали!
Пора было выходить из Машины.
Джунгли были высокие, и джунгли были широкие, и джунгли были навеки всем миром. Воздух наполняли звуки, словно музыка, словно паруса бились в воздухе - это летели, будто исполинские летучие мыши из кошмара, из бреда, махая огромными, как пещерный свод, серыми крыльями, птеродактили. Экельс, стоя на узкой Тропе, шутя прицелился.
- Эй, бросьте! - скомандовал Тревис. - Даже в шутку не цельтесь, черт бы вас побрал! Вдруг выстрелит...
Экельс покраснел.
- Где же наш Tyrannosaurus rex?
Лесперанс взглянул на свои часы.
- На подходе. Мы встретимся ровно через шестьдесят секунд. И ради бога - не прозевайте красное пятно. Пока не скажем, не стрелять. И не сходите с Тропы. Не сходите с тропы!
Они шли навстречу утреннему ветерку.
- Странно, - пробормотал Экельс. - Перед нами - шестьдесят миллионов лет. Выборы прошли. Кейт стал президентом. Все празднуют победу. А мы - здесь, все эти миллионы лет словно ветром сдуло, их нет. Всего того, что заботило нас на протяжении нашей жизни, еще нет и в помине, даже в проекте.
- Приготовиться! - скомандовал Тревис. - Первый выстрел ваш, Экельс. Биллингс - второй номер. За ним - Кремер.
- Я охотился на тигров, кабанов, буйволов, слонов, но видит бог - это совсем другое дело, - произнес Экельс. - Я дрожу, как мальчишка.
- Тихо, - сказал Тревис.
Все остановились.
Тревис поднял руку.
- Впереди, - прошептал он. - В тумане. Он там. Встречайте Его Королевское Величество.
Безбрежные джунгли были полны щебета, шороха, бормотанья, вздохов.
Вдруг все смолкло, точно кто-то затворил дверь.
Тишина.
Раскат грома.
Из мглы ярдах в ста впереди появился Tyrannosaurus rex.
- Силы небесные, - пролепетал Экельс.
- Тсс!
Оно шло на огромных, лоснящихся, пружинящих, мягко ступающих ногах.
Оно за тридцать футов возвышалось над лесом - великий бог зла, прижавший хрупкие руки часовщика к маслянистой груди рептилии. Ноги - могучие поршни, тысяча фунтов белой кости, оплетенные тугими каналами мышц под блестящей морщинистой кожей, подобной кольчуге грозного воина. Каждое бедро - тонна мяса, слоновой кости и кольчужной стали. А из громадной вздымающейся грудной клетки торчали две тонкие руки, руки с пальцами, которые могли подобрать и исследовать человека, будто игрушку. Извивающаяся змеиная шея легко вздымала к небу тысячекилограммовый каменный монолит головы. Разверстая пасть обнажала частокол зубов-кинжалов. Вращались глаза - страусовые яйца, не выражая ничего, кроме голода. Оно сомкнуло челюсти в зловещем оскале. Оно побежало, и задние ноги смяли кусты и деревья, и когти вспороли сырую землю, оставляя следы шестидюймовой глубины. Оно бежало скользящим балетным шагом, неправдоподобно уверенно и легко для десятитонной махины. Оно настороженно вышло на залитую солнцем прогалину и пощупало воздух своими красивыми чешуйчатыми руками.
- Господи! - Губы Экельса дрожали. - Да оно, если вытянется, луну достать может.
- Тсс! - сердито зашипел Тревис. - Он еще не заметил нас.
- Его нельзя убить. - Экельс произнес это спокойно, словно заранее отметал все возражения. Он взвесил показания очевидцев и вынес окончательное решение. Ружье в его руках было словно пугач. - Идиоты, и что нас сюда принесло... Это же невозможно.
- Молчать! - рявкнул Тревис.
- Кошмар...
- Кру-гом! - скомандовал Тревис. - Спокойно возвращайтесь в Машину. Половина суммы будет вам возвращена.
- Я не ждал, что оно окажется таким огромным, - сказал Экельс. - Одним словом, просчитался. Нет, я участвовать не буду.
- Оно заметило нас!
- Вон красное пятно на груди!
Громогласный Ящер выпрямился. Его бронированная плоть сверкала, словно тысяча зеленых монет. Монеты покрывала жаркая слизь. В слизи копошились мелкие козявки, и все тело переливалось, будто по нему пробегали волны, даже когда чудовище стояло неподвижно. Оно глухо дохнуло. Над поляной повис запах сырого мяса.
- Помогите мне уйти, - сказал Экельс. - Раньше все было иначе. Я всегда знал, что останусь жив. Были надежные проводники, удачные сафари, никакой опасности. На сей раз я просчитался. Это мне не по силам. Признаюсь. Орешек мне не по зубам.
- Не бегите, - сказал Лесперанс. - Повернитесь кругом. Спрячьтесь в Машине.
- Да. - Казалось, Экельс окаменел. Он поглядел на свои ноги, словно пытался заставить их двигаться. Он застонал от бессилия.
- Экельс!
Он сделал шаг - другой, зажмурившись, волоча ноги.
- Не в ту сторону!
Едва он двинулся с места, как чудовище с ужасающим воем ринулось вперед. Сто ярдов оно покрыло за четыре секунды. Ружья взметнулись вверх и дали залп. Из пасти зверя вырвался ураган, обдав людей запахом слизи и крови. Чудовище взревело, его зубы сверкали на солнце.
Не оглядываясь, Экельс слепо шагнул к краю Тропы, сошел с нее и, сам того не сознавая, направился в джунгли; ружье бесполезно болталось в руках. Ступни тонули в зеленом мху, ноги влекли его прочь, он чувствовал себя одиноким и далеким от того, что происходило за его спиной.
Снова затрещали ружья. Выстрелы потонули в громовом реве ящера. Могучий хвост рептилии дернулся, точно кончик бича, и деревья взорвались облаками листьев и веток. Чудовище протянуло вниз свои руки ювелира - погладить людей, разорвать их пополам, раздавить, как ягоды, и сунуть в пасть, в ревущую глотку! Глыбы глаз очутились возле людей. Они увидели свое отражение. Они открыли огонь по металлическим векам и пылающим черным зрачкам.
Словно каменный идол, словно горный обвал, рухнул. Tyrannosaurus rex.
Рыча, он цеплялся за деревья и валил их. Зацепил и смял металлическую Тропу. Люди бросились назад, отступая. Десять тонн холодного мяса, как утес, грохнулись оземь. Ружья дали еще залп. Чудовище ударило бронированным хвостом, щелкнуло змеиными челюстями и затихло. Из горла фонтаном била кровь. Где-то внутри лопнул бурдюк с жидкостью, и зловонный поток захлестнул охотников. Они стояли неподвижно, облитые чем-то блестящим, красным.
Гром смолк.
В джунглях воцарилась тишина. После обвала - зеленый покой. После кошмара - утро.
Биллингс и Кремер сидели на Тропе; им было плохо. Тревис и Лесперанс стояли рядом, держа дымящиеся ружья и чертыхаясь.
Экельс, весь дрожа, лежал ничком в Машине Времени. Каким-то образом он выбрался обратно на Тропу и добрел до Машины.
Подошел Тревис, глянул на Экельса, достал из ящика марлю и вернулся к тем, что сидели на Тропе.
- Оботритесь.
Они стерли со шлемов кровь. И тоже принялись чертыхаться. Чудовище лежало неподвижно. Гора мяса, из недр которой доносилось бульканье, вздохи - это умирали клетки, органы переставали действовать, и соки последний раз текли по своим ходам, все отключалось, навсегда выходя из строя. Точно вы стояли возле разбитого паровоза или закончившего рабочий день парового катка - все клапаны открыты или плотно зажаты. Затрещали кости: вес мышц, ничем не управляемый - мертвый вес, - раздавил тонкие руки, притиснутые к земле. Колыхаясь, оно приняло покойное положение.
Вдруг снова грохот. Высоко над ними сломался исполинский сук. С гулом он обрушился на безжизненное чудовище, как бы окончательно утверждая его гибель.
- Так. - Лесперанс поглядел на часы. - Минута в минуту. Это тот самый сук, который должен был его убить. - Он обратился к двум охотникам. - Фотография трофея вам нужна?
- Что?
- Мы не можем увозить добычу в Будущее. Туша должна лежать здесь, на своем месте, чтобы ею могли питаться насекомые, птицы, бактерии. Равновесие нарушать нельзя. Поэтому добычу оставляют. Но мы можем сфотографировать вас возле нее.
Охотники сделали над собой усилие, пытаясь думать, но сдались, тряся головой.
Они послушно дали отвести себя в Машину. Устало опустились на сиденья. Тупо оглянулись на поверженное чудовище - немой курган. На остывающей броне уже копошились золотистые насекомые, сидели причудливые птицеящеры.
Внезапный шум заставил охотников оцепенеть: на полу Машины, дрожа, сидел Экельс.
- Простите меня, - сказал он.
- Встаньте! - рявкнул Тревис.
Экельс встал.
- Ступайте на Тропу, - скомандовал Тревис. Он поднял ружье. - Вы не вернетесь с Машиной. Вы останетесь здесь!
Лесперанс перехватил руку Тревиса.
- Постой...
- А ты не суйся! - Тревис стряхнул его руку. - Из-за этого подонка мы все чуть не погибли. Но главное даже не это. Нет, черт возьми, ты погляди на его башмаки! Гляди! Он соскочил с Тропы. Понимаешь, чем это нам грозит? Один бог знает, какой штраф нам прилепят! Десятки тысяч долларов! Мы гарантируем, что никто не сойдет с Тропы. Он сошел. Идиот чертов! Я обязан доложить правительству. И нас могут лишить концессии на эти сафари. А какие последствия будут для Времени, для Истории?!
- Успокойся, он набрал на подошвы немного грязи - только и всего.
- Откуда мы можем знать? - крикнул Тревис. - Мы ничего не знаем! Это же все сплошная загадка! Шагом марш, Экельс!
Экельс полез в карман.
- Я заплачу сколько угодно. Сто тысяч долларов! Тревис покосился на чековую книжку и плюнул.
- Ступайте! Чудовище лежит возле Тропы. Суньте ему руки по локоть в пасть. Потом можете вернуться к нам.
- Это несправедливо!
- Зверь мертв, ублюдок несчастный. Пули! Пули не должны оставаться здесь, в Прошлом. Они могут повлиять на развитие. Вот вам нож. Вырежьте их!
Джунгли опять пробудились к жизни и наполнились древними шорохами, птичьими голосами. Экельс медленно повернулся и остановил взгляд на доисторической падали, глыбе кошмаров и ужасов. Наконец, словно лунатик, побрел по Тропе.
Пять минут спустя он, дрожа всем телом, вернулся к Машине, его руки были по локоть красны от крови.
Он протянул вперед обе ладони. На них блестели стальные пули. Потом он упал. Он лежал там, где упал недвижимый.
- Напрасно ты его заставил это делать, - сказал Лесперанс.
- Напрасно! Об этом рано судить. - Тревис толкнул неподвижное тело. - Не помрет. Больше его не потянет за такой добычей. А теперь, - он сделал вялый жест рукой, - включай. Двигаемся домой.
1492. 1776. 1812
Они умыли лицо и руки. Они сняли заскорузлые от крови рубахи, брюки и надели все чистое. Экельс пришел в себя, но сидел молча. Тревис добрых десять минут в упор смотрел на него.
- Не глядите на меня, - вырвалось у Экельса. - Я ничего не сделал.
- Кто знает.
- Я только соскочил с Тропы и вымазал башмаки глиной. Чего вы от меня хотите? Чтобы я вас на коленях умолял?
- Это не исключено. Предупреждаю Вас, Экельс, может еще случиться, что я вас убью. Ружье заряжено.
- Я не виноват. Я ничего не сделал.
1999. 2000. 2055.
Машина остановилась.
- Выходите, - скомандовал Тревис.
Комната была такая же, как прежде. Хотя нет, не совсем такая же. Тот же человек сидел за той же конторкой. Нет, не совсем тот же человек, и конторка не та же.
Тревис быстро обвел помещение взглядом.
- Все в порядке? - буркнул он.
- Конечно. С благополучным возвращением!
Но настороженность не покидала Тревиса. Казалось, он проверяет каждый атом воздуха, придирчиво исследует свет солнца, падающий из высокого окна.
- О'кей, Экельс, выходите. И больше никогда не попадайтесь мне на глаза.
Экельс будто окаменел.
- Ну? - поторопил его Тревис. - Что вы там такое увидели?
Экельс медленно вдыхал воздух - с воздухом что-то произошло, какое-то химическое изменение, настолько незначительное, неуловимое, что лишь слабый голос подсознания говорил Экельсу о перемене. И краски - белая, серая, синяя, оранжевая, на стенах, мебели, в небе за окном - они... они... да: что с ними случилось? А тут еще это ощущение. По коже бегали мурашки. Руки дергались. Всеми порами тела он улавливал нечто странное, чужеродное. Будто где-то кто-то свистнул в свисток, который слышат только собаки. И его тело беззвучно откликнулось. За окном, за стенами этого помещения, за спиной человека (который был не тем человеком) у перегородки (которая была не той перегородкой) - целый мир улиц и людей. Но как отсюда определить, что это за мир теперь, что за люди? Он буквально чувствовал, как они движутся там, за стенами, - словно шахматные фигурки, влекомые сухим ветром...
Зато сразу бросалось в глаза объявление на стене, объявление, которое он уже читал сегодня, когда впервые вошел сюда.
Что-то в нем было не так.
А/О СОФАРИ ВОВРЕМЕНИ
АРГАНИЗУЕМ СОФАРИ ВЛЮБОЙ ГОД ПРОШЛОГО
ВЫ ВЫБЕРАЕТЕ ДАБЫЧУ
МЫ ДАСТАВЛЯЕМ ВАС НАМЕСТО
ВЫ УБЕВАЕТЕ ЕЕ
Экельс почувствовал, что опускается на стул. Он стал лихорадочно скрести грязь на башмаках. Его дрожащая рука подняла липкий ком.
- Нет, не может быть! Из-за такой малости... Нет!
На комке было отливающее зеленью, золотом и чернью пятно - бабочка, очень красивая... мертвая.
- Из-за такой малости! Из-за бабочки! - закричал Экельс.
Она упала на пол - изящное маленькое создание, способное нарушить равновесие, повалились маленькие костяшки домино... большие костяшки... огромные костяшки, соединенные цепью неисчислимых лет, составляющих Время. Мысли Экельса смещались. Не может быть, чтобы она что-то изменила. Мертвая бабочка - и такие последствия? Невозможно!
Его лицо похолодело Непослушными губами он вымолвил:
- Кто... кто вчера победил на выборах?
Человек за конторкой хихикнул.
- Шутите? Будто не знаете! Дойчер, разумеется! Кто же еще? Уж не этот ли хлюпик Кейт? Теперь у власти железный человек! - Служащий опешил. - Что это с вами?
Экельс застонал. Он упал на колени. Дрожащие пальцы протянулись к золотистой бабочке.
- Неужели нельзя, - молил он весь мир, себя, служащего, Машину, - вернуть ее туда, оживить ее? Неужели нельзя начать все сначала? Может быть...
Он лежал неподвижно. Лежал, закрыв глаза, дрожа, и ждал. Он отчетливо слышал тяжелое дыхание Тревиса, слышал, как Тревис поднимает ружье и нажимает курок.
И грянул гром.
1952
|
|
Дневник Chaos_Theory |
Все, что интересует меня. В данный момент времени или всегда.
Рассказы. Моя жизнь или чужая. Теория Хаоса, Эффект бабочки. Психология и журналистика. Это сейчас, а что потом?
Рассказы. Моя жизнь или чужая. Теория Хаоса, Эффект бабочки. Психология и журналистика. Это сейчас, а что потом?
|
|






