Введение

В технике явление формирования поверхности вращающейся жидкости в форме близкой к поверхности параболоида вращения используется в основном в сепарирующих центрифугах для разделения суспензий на фракции [1].

Меня заинтересовал так называемый жидкостной тахометр. Принцип работы прибора состоит в контроле за уровнем верхней кромки жидкости во вращающемся цилиндрическом стакане.
Уровень жидкости зависит от скорости вращения стакана и может контролироваться простой оптической следящей системой.

Рассмотрение математической модели такого прибора имеет не только познавательный, но и практический интерес с учётом её реализации средствами свободно распространяемого языка общего назначения Python.

Теория – просто и кратко

Вектора сил, действующих на частицу жидкости во вращающемся цилиндрическом стакане приведены на следующем рисунке.



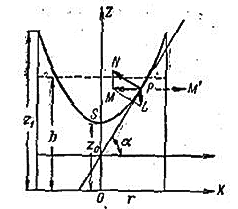
Рассмотрим сечение поверхности вращения координатной плоскостью ZX и найдём касательную в точке P (x, z) этого сечения. На частицу Q находящуюся в точке P действует сила тяжести mg изображённая в виде вектора PL.

Давление жидкости изображено в виде вектора PN направленного нормально к поверхности жидкости. Силы PM и PM’ для установившегося движения равны. Частица жидкости движется по окружности радиуса x её ускорение PM направлено к центру вращения и равно m*w**2 *x. Читать дальше ->

https://habrahabr.ru/post/339562/