Бродя по бескрайним просторам Youtube нашел интересный видеоролик, который посвящен решению следующего уравнения с параметром.

Найти все значения параметра а, при которых уравнение х² - (4а - 2)|х| + 3а² - 2а = 0 имеет ровно два корня.

Для этой задачи я нашел еще два решения, которые отличаются от того, которое привел автор упоминаемого ролика.

Решение I.

Так как левая часть уравнения четная функция, то уравнение х² - (4а - 2)|х| + 3а² - 2а = 0 может иметь два решения только тогда, когда уравнение t² - (4а - 2)t + 3а² - 2а = 0 имеет единственное положительное решение либо тогда, когда уравнение t² - (4а - 2)t + 3а² - 2а = 0 имеет два корня разных знаков.

Рассмотри первый случай (уравнение t² - (4а - 2)t + 3а² - 2а = 0 имеет единственное положительное решение). В этом случае дискриминант этого уравнения равен нулю.

D = (2a - 1)² - (3а² - 2а) = 4а² - 4a + 1 - а² + 2а = а² - 2a + 1 = (a - 1)² = 0, a = 1. Тогда наше уравнение примет вид х² - 2|х| + 1 = 0, (|х| - 1) = 0, |х| = 1, х = ±1. Действительно, наше уравнение имеет ровно два корня.

Во втором случае (уравнение t² - (4а - 2)t + 3а² - 2а = 0) необходимо и достаточно чтобы выполнялось неравенство 3а² - 2а < 0, a(3a - 2) < 0. последнее неравенство имеет решение (0; 2/3).

nnfr? уравнение х² - (4а - 2)|х| + 3а² - 2а = 0 имеет ровно два корня при а ∈ (0; 2/3) ∪ {1}.

Ответ: а ∈ (0; 2/3) ∪ {1}.

Решение II.

Решим уравнение х² - (4а - 2)|х| + 3а² - 2а = 0. Пусть |х| = t.

t² - (4а - 2)t + 3а² - 2а = 0

Нетрудно заметить, что свободный член этого уравнения равен 3а² - 2а = а(3а - 2). При этом а + (3а - 2) = 4а - 2 - второй коэффициент с противоположным знаком. Значит, t = a или t = 3a - 2. Поэтому наше уравнение равносильно совокупности



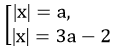
Понятно, что эта совокупность уравнений имеет ровно два решения лишь только в том случае, когда а = 3а - 2 и оба числа а и 3а - 2 положительны или а < 0 и 3а - 2 > 0 или а > 0 и 3а - 2 < 0. Во всех остальных случаях эта система либо не имеет решений, либо количество ее решений не равно двум.




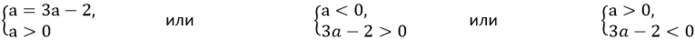
Первая система имеет решение а = 1. Вторая система не имеет решений, а решением третьей системы будет промежуток (0; 2/3). Поэтому решением совокупности будет множество (0; 2/3) ∪ {1}.

Ответ: а ∈ (0; 2/3) ∪ {1}.

Есть и третье решение нашего неравенства. Это решение я предлагаю посмотреть вот в этом видеоролике.



Это решение, которое предложил Никита мне понравилось. Оно наглядное. Однако есть один недостаток, решения предложенные мною требуют меньше времени. Но это только мое субъективное мнение.