-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Задача на отношение площадей трапеции (типа С4) |
C4.Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2: 3. Найти длину отрезка этой прямой, заключенного внутри трапеции.
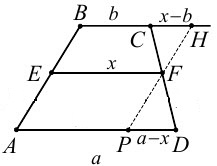
Решение. Неизвестно как относятся площади трапеций BCFE и AEFD - как 2:3 или как 3:2.
Поэтому эту задачу будем решать в общем виде.
Обозначим искомый отрезок ЕF через х. Пусть площади трапеций BCFE и AEFD относятся как m:n.
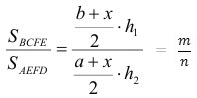 . Отсюда
. Отсюда 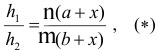
где h1 и h2 - высоты этих трапеций.
Через точку F проведем отрезок РН параллельно АВ (можно было бы этот отрезок провести через точку С или D). Тогда треугольники PFD и CHF подобны (докажите самостоятельно) и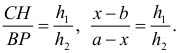
Используем соотношение (*):
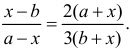
Решая полученное уравнение относительно переменной х, получаем m(х² - b²) = n(a² - x²), (m + n)x² = na² + mb²,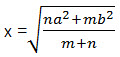 .
.
Если площади трапеций BCFE и AEFD относятся как 2:3, то m = 2, n = 3 и искомый ответ будет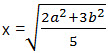 .
.
Если же площади трапеций BCFE и AEFD относятся как 3:2, то m = 3, n = 2 и искомый ответ будет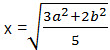
Ответ: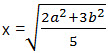 или
или 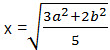 .
.

Решение. Неизвестно как относятся площади трапеций BCFE и AEFD - как 2:3 или как 3:2.
Поэтому эту задачу будем решать в общем виде.
Обозначим искомый отрезок ЕF через х. Пусть площади трапеций BCFE и AEFD относятся как m:n.
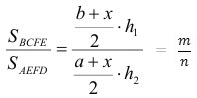 . Отсюда
. Отсюда 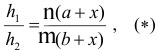
где h1 и h2 - высоты этих трапеций.
Через точку F проведем отрезок РН параллельно АВ (можно было бы этот отрезок провести через точку С или D). Тогда треугольники PFD и CHF подобны (докажите самостоятельно) и
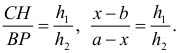
Используем соотношение (*):
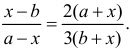
Решая полученное уравнение относительно переменной х, получаем m(х² - b²) = n(a² - x²), (m + n)x² = na² + mb²,
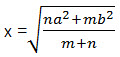 .
.Если площади трапеций BCFE и AEFD относятся как 2:3, то m = 2, n = 3 и искомый ответ будет
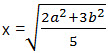 .
.Если же площади трапеций BCFE и AEFD относятся как 3:2, то m = 3, n = 2 и искомый ответ будет
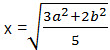
Ответ:
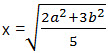 или
или 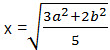 .
.
| Рубрики: | Решения тестов ЕГЭ Решения задач |
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |






