-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Целые числа в тестах ЕГЭ |
В этой заметке будет рассказано о решении тестового задания типа С5, связанного с целыми числами из варианта для подготовки 2012 года.
При каких значениях х оба числа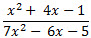 и
и 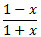 целые?
целые?
Решение. Пусть а =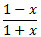 , b =
, b = 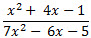 . Тогда
. Тогда
a(1 + x) = 1 - x,
x(a + 1) = 1 - a,
x =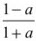 (a ≠ 1).
(a ≠ 1).
Тогда b =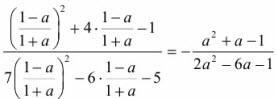 .
.
Переформулируем условие задачи "в терминах а и b".
Выясним при каких целых значениях а ≠ 1 рациональная дробь -b =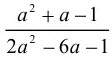 принимает только целые значения?
принимает только целые значения?
Очевидно, что модуль числителя последней дроби должен быть не меньше модуля знаменателя этой дроби.
∣a2 + a - 1∣ ≥ ∣2а2 - 6a - 1∣,
(a2 + a - 1)2 ≥ (2а2 - 6a - 1)2,
(a2 + a - 1)2 - (2а2 - 6a - 1)2 ≥ 0,
(a2 - 7a)(3a2 - 5a - 2) ≥ 0,
Разложив трехчлен 3a2 - 5a - 2 на множители получим
a(a - 7)(3a + 1)(a - 2) ≥ 0,
a ∈ [-1/3; 0} ∪ [2; 7]. Так как а - целое число, то а ∈ {0; 2; 3; 4; 5; 6; 7} .
При а = 0 b = -1 и x = 1
При а = 2 b = 1 и x = -1/3
При а = 3 b = -11 и x = -1/2
При а = 4 b = 19/20
При а = 5 b = 29/19
При а = 6 b = 41/35
При а = 7 b = 1 и x = -3/4
Ответ: 1; -1/3; -1/2; -3/4.
Это задание будет трудным только тем учащимся, которые не имеют соответствующего опыта решения подобных задач.
Такие задачи практически не встречаются в школьных учебниках. Как может рядовой учитель научит своих питомцев их решать, если у него нет соответствующего набора таких задач. Если приемы конструирования таких упражнений? Ответ на этот вопрос мне не известен. Однако, думаю, что такие приемы можно придумать.
При каких значениях х оба числа
Решение. Пусть а =
a(1 + x) = 1 - x,
x(a + 1) = 1 - a,
x =
Тогда b =
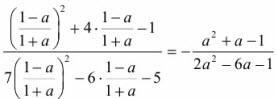 .
.Переформулируем условие задачи "в терминах а и b".
Выясним при каких целых значениях а ≠ 1 рациональная дробь -b =
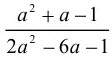 принимает только целые значения?
принимает только целые значения?Очевидно, что модуль числителя последней дроби должен быть не меньше модуля знаменателя этой дроби.
∣a2 + a - 1∣ ≥ ∣2а2 - 6a - 1∣,
(a2 + a - 1)2 ≥ (2а2 - 6a - 1)2,
(a2 + a - 1)2 - (2а2 - 6a - 1)2 ≥ 0,
(a2 - 7a)(3a2 - 5a - 2) ≥ 0,
Разложив трехчлен 3a2 - 5a - 2 на множители получим
a(a - 7)(3a + 1)(a - 2) ≥ 0,
a ∈ [-1/3; 0} ∪ [2; 7]. Так как а - целое число, то а ∈ {0; 2; 3; 4; 5; 6; 7} .
При а = 0 b = -1 и x = 1
При а = 2 b = 1 и x = -1/3
При а = 3 b = -11 и x = -1/2
При а = 4 b = 19/20
При а = 5 b = 29/19
При а = 6 b = 41/35
При а = 7 b = 1 и x = -3/4
Ответ: 1; -1/3; -1/2; -3/4.
Это задание будет трудным только тем учащимся, которые не имеют соответствующего опыта решения подобных задач.
Такие задачи практически не встречаются в школьных учебниках. Как может рядовой учитель научит своих питомцев их решать, если у него нет соответствующего набора таких задач. Если приемы конструирования таких упражнений? Ответ на этот вопрос мне не известен. Однако, думаю, что такие приемы можно придумать.
| Рубрики: | Решения тестов ЕГЭ Решения задач |
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |






