Анализируем карьеру игроков NHL с помощью Survival Regression и Python |
Привет, Хабр! Сегодня рассмотрим один из подходов к оценке временного риска, который основан на кривой выживаемости и одноименной регрессии, и применим его к анализу продолжительности карьеры игроков НХЛ.
Когда у данного пациента произойдет рецидив? Когда наш клиент уйдет? Ответы на подобные вопросы можно найти с помощью анализа выживания, который может быть использован во всех областях, где исследуется временной промежуток от «рождения» до «смерти» объекта, либо аналогичные события: период от поступления оборудования до его выхода из строя, от начала использования услуг компании и до отказа от них и т.д. Чаще всего данные модели используются в медицине, где необходимо оценить риск летального исхода у больного, чем и обусловлено название модели, однако они также применимы в сфере производства, банковском и страховом секторах.

Очевидно, что среди рассматриваемых объектов всегда будут те, для которых «смерть» (выход из строя, наступление страхового случая) еще не произошла, и не учитывать их — распространенная ошибка среди аналитиков, поскольку в этом случае они не включают в выборку наиболее актуальную информацию и могут искусственно занизить временной интервал. Для решения данной проблемы был разработан анализ выживаемости, который оценивает потенциальную «продолжительность жизни» наблюдений с еще не наступившей «смертью».
Выше мы говорили о применении данного подхода в медицине и экономике, однако сейчас рассмотрим менее тривиальный пример — продолжительность карьеры игроков НХЛ. Все мы знаем, что хоккей — очень динамичная и непредсказуемая игра, где ты можешь, как Горди Хоу (26 сезонов) долгие годы играть на высочайшем уровне, а можешь из-за неудачного столкновения завершить карьеру после пары сезонов. Поэтому выясним: сколько сезонов может ожидать провести в НХЛ хоккеист и какие факторы влияют на продолжительность карьеры?
Посмотрим на уже очищенные и готовые для анализа данные:
Были собраны данные по 688 хоккеистам НХЛ, выступавших с 1979 года и сыгравших не менее 20 матчей, их позиции на поле, количеству набранных очков, пользе команде (±), началу карьеры в НХЛ и ее продолжительности. Столбец observed показывает, завершил ли игрок карьеру, то есть игроки со значением 0 все еще выступают в лиге.
Посмотрим на распределение игроков по количеству сыгранных сезонов:
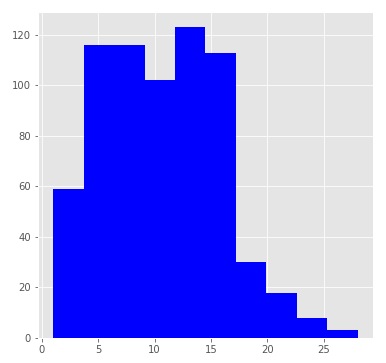
Распределение похоже на логнормальное с медианой в 11 сезонов. Данная статистика учитывает лишь сыгранное до 2017 года количество сезонов действующими игроками, поэтому медианная оценка явно занижена.
Чтобы получить более точное значение, оценим функцию выживаемости с помощью библиотеки lifelines:
Синтаксис библиотеки схож с scikit-learn и ее fit/predict: инициировав KaplanMeierFitter мы затем обучаем модель на данных. В качестве аргумента метод fit принимает временной интервал career_length и вектор observed.
Наконец, когда модель обучена, мы можем построить функцию выживаемости для игроков НХЛ:
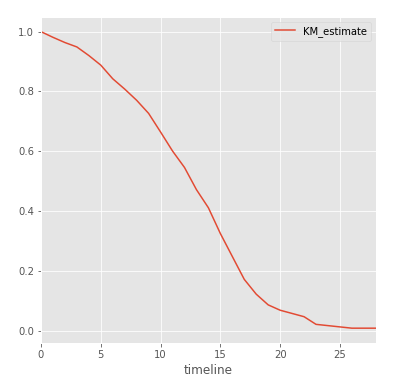
Каждая точка графика — вероятность того, что игрок сыграет больше t сезонов. Как видно, рубеж в 6 сезонов преодолевают 80% игроков, в то время как совсем небольшому числу игроков удается сыграть больше 17 сезонов в НХЛ. Теперь более строго:
Таким образом, 50% игроков НХЛ сыграют больше 13 сезонов, что на 2 сезона больше чем первоначальная оценка. Шансы хоккеистов сыграть больше 5 и 20 сезонов равны 88,8% и 6,9% соответственно. Отличный стимул для молодых игроков!
Мы также можем вывести функцию выживаемости, вместе с доверительными интервалами для вероятности:
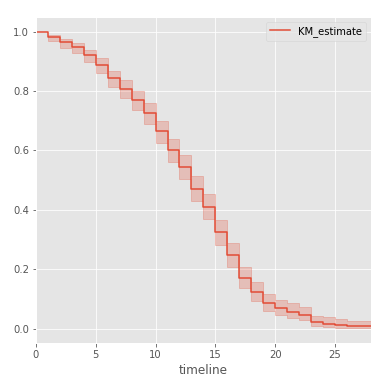
Аналогично построим функцию угрозы, используя процедуру Нельсона-Аалена:
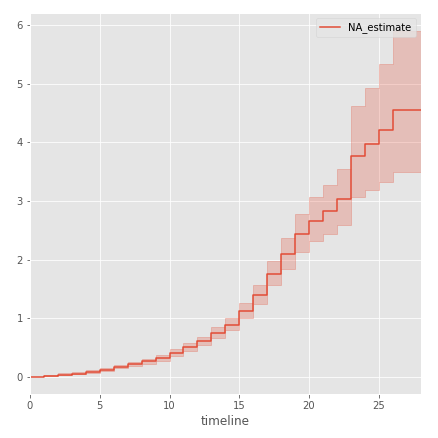
Как видно на графике, в течение первых 10 лет риск у игрока НХЛ завершить карьеру в конце сезона крайне мал, однако после 10 сезона резко данный риск резко возрастает. Иначе говоря, проведя 10 сезонов в НХЛ, игрок будет все чаще задумываться о том, чтобы завершить карьеру.
Теперь сравним продолжительность карьеры защитника и нападающего НХЛ. Изначально предполагаем, что нападающие в среднем играют намного дольше, чем защитники, поскольку они чаще всего более популярны среди болельщиков, поэтому чаще получают многолетние контракты. Также с возрастом игроки становятся медленными, что больнее всего бьет по защитникам, которым все сложнее справляться с юркими нападающими.
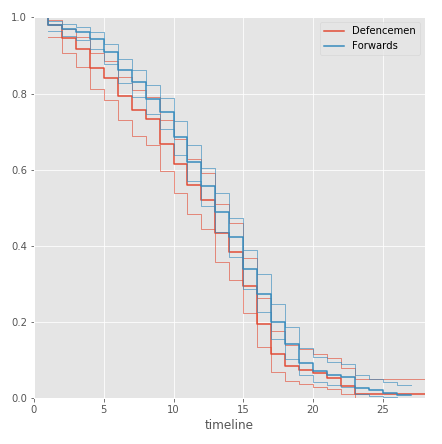
Похоже, что продолжительность карьеры защитников чуть короче, чем у нападающих. Чтобы удостовериться в верности вывода проведем статистический тест на основе критерия хи-квадрат:
Итак, на 10% уровне значимости отвергаем нулевую гипотезу: защитники действительно имеют больший шанс завершить карьеру раньше, чем нападающие, при этом, как видно по графику, ближе к концу карьеры разница увеличивается, что также подтверждает выдвинутый ранее тезис: старый защитник все меньше успевает за игрой и становится все менее востребован.
Зачастую у нас также имеются и другие факторы, влияющие на продолжительность «жизни», которые мы бы хотели учесть. Для этого была разработана модель регрессии выживаемости, которая, как и классическая линейная регрессия имеет зависимую переменную и набор факторов.
Рассмотрим один из популярных подходов к оценке параметров регрессии — аддитивную модель Аалена, который в качестве зависимой переменной выбрал не сами временные интервалы, а рассчитанные на их основе значения функции угрозы :
Перейдем к реализации модели. В качестве факторов модели примем количество очков, позицию игрока, дату начала карьеры и общую полезность команде (±):
Теперь, когда все готово, обучим регрессию выживаемости:
Попробуем оценить, сколько еще сезонов отыграют в НХЛ 2 игрока: Дерек Степан, нападающий, который начал свою карьеру в 2010 году и набрал 310 очков с показателем полезности +109 и сравним его с менее успешным игроком НХЛ — Класом Дальбеком, который попал в НХЛ в 2014 году, набрал 11 очков с показателем полезности -12.
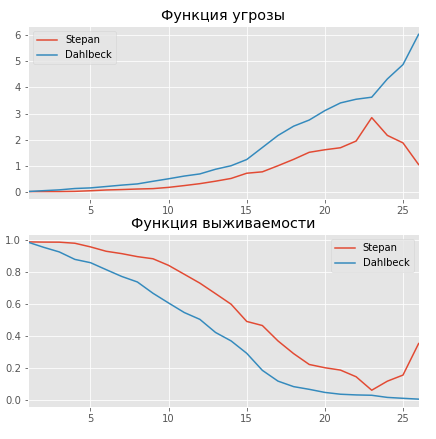
Как и ожидалось, у более успешного игрока ожидаемая продолжительность карьеры выше. Так, у Степана вероятность сыграть больше 11 сезонов — 80%, в то время как у Дальбека — всего 55%. Также по кривой угрозы видно, что начиная с 13 сезона резко возрастает риск завершить карьеру на следующий сезон, причем у Дальбека он растет быстрее, чем у Степана.
Чтобы более строго оценить качество регрессии используем встроенную в библиотеку lifelines процедуру кросс-валидации. При этом, работая с цензурированными данными, мы не можем использовать в качестве метрики качества среднеквадратическую ошибку и подобные критерии, поэтому в библиотеки используется concordance index или индекс согласия, который является обобщением AUC-метрики. Проведем 5-шаговую кросс-валидацию:
Средняя точность по всем итерациям равна 76,4% с отклонением в 2,7%, что говорит о достаточно неплохом качестве алгоритма.

Метки:
author a-pichugin
машинное обучение
data mining
big data
блог компании new professions lab
nhl
кривые дожития
survival analysis
Когда у данного пациента произойдет рецидив? Когда наш клиент уйдет? Ответы на подобные вопросы можно найти с помощью анализа выживания, который может быть использован во всех областях, где исследуется временной промежуток от «рождения» до «смерти» объекта, либо аналогичные события: период от поступления оборудования до его выхода из строя, от начала использования услуг компании и до отказа от них и т.д. Чаще всего данные модели используются в медицине, где необходимо оценить риск летального исхода у больного, чем и обусловлено название модели, однако они также применимы в сфере производства, банковском и страховом секторах.

Очевидно, что среди рассматриваемых объектов всегда будут те, для которых «смерть» (выход из строя, наступление страхового случая) еще не произошла, и не учитывать их — распространенная ошибка среди аналитиков, поскольку в этом случае они не включают в выборку наиболее актуальную информацию и могут искусственно занизить временной интервал. Для решения данной проблемы был разработан анализ выживаемости, который оценивает потенциальную «продолжительность жизни» наблюдений с еще не наступившей «смертью».
Анализ карьеры игроков NHL
Данные и построение кривой выживаемости
Выше мы говорили о применении данного подхода в медицине и экономике, однако сейчас рассмотрим менее тривиальный пример — продолжительность карьеры игроков НХЛ. Все мы знаем, что хоккей — очень динамичная и непредсказуемая игра, где ты можешь, как Горди Хоу (26 сезонов) долгие годы играть на высочайшем уровне, а можешь из-за неудачного столкновения завершить карьеру после пары сезонов. Поэтому выясним: сколько сезонов может ожидать провести в НХЛ хоккеист и какие факторы влияют на продолжительность карьеры?
Посмотрим на уже очищенные и готовые для анализа данные:
df.head(3)| Name | Position | Points | Balance | Career_start | Career_length | Observed |
|---|---|---|---|---|---|---|
| Olli Jokinen | F | 419 | -58 | 1997 | 18 | 1 |
| Kevyn Adams | F | 72 | -14 | 1997 | 11 | 1 |
| Matt Pettinger | F | 99 | -44 | 2000 | 10 | 1 |
Были собраны данные по 688 хоккеистам НХЛ, выступавших с 1979 года и сыгравших не менее 20 матчей, их позиции на поле, количеству набранных очков, пользе команде (±), началу карьеры в НХЛ и ее продолжительности. Столбец observed показывает, завершил ли игрок карьеру, то есть игроки со значением 0 все еще выступают в лиге.
Посмотрим на распределение игроков по количеству сыгранных сезонов:
Распределение похоже на логнормальное с медианой в 11 сезонов. Данная статистика учитывает лишь сыгранное до 2017 года количество сезонов действующими игроками, поэтому медианная оценка явно занижена.
Чтобы получить более точное значение, оценим функцию выживаемости с помощью библиотеки lifelines:
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(df.career_length, event_observed = df.observed)
Out:Синтаксис библиотеки схож с scikit-learn и ее fit/predict: инициировав KaplanMeierFitter мы затем обучаем модель на данных. В качестве аргумента метод fit принимает временной интервал career_length и вектор observed.
Наконец, когда модель обучена, мы можем построить функцию выживаемости для игроков НХЛ:
kmf.survival_function_.plot()Каждая точка графика — вероятность того, что игрок сыграет больше t сезонов. Как видно, рубеж в 6 сезонов преодолевают 80% игроков, в то время как совсем небольшому числу игроков удается сыграть больше 17 сезонов в НХЛ. Теперь более строго:
print(kmf.median_)
print(kmf.survival_function_.KM_estimate[20])
print(kmf.survival_function_.KM_estimate[5])Out:13.0
0.0685611305647
0.888063315225Таким образом, 50% игроков НХЛ сыграют больше 13 сезонов, что на 2 сезона больше чем первоначальная оценка. Шансы хоккеистов сыграть больше 5 и 20 сезонов равны 88,8% и 6,9% соответственно. Отличный стимул для молодых игроков!
Мы также можем вывести функцию выживаемости, вместе с доверительными интервалами для вероятности:
kmf.plot()Аналогично построим функцию угрозы, используя процедуру Нельсона-Аалена:
from lifelines import NelsonAalenFitter
naf = NelsonAalenFitter()
naf.fit(df.career_length,event_observed=df.observed)
naf.plot()Как видно на графике, в течение первых 10 лет риск у игрока НХЛ завершить карьеру в конце сезона крайне мал, однако после 10 сезона резко данный риск резко возрастает. Иначе говоря, проведя 10 сезонов в НХЛ, игрок будет все чаще задумываться о том, чтобы завершить карьеру.
Сравнение нападающих и защитников
Теперь сравним продолжительность карьеры защитника и нападающего НХЛ. Изначально предполагаем, что нападающие в среднем играют намного дольше, чем защитники, поскольку они чаще всего более популярны среди болельщиков, поэтому чаще получают многолетние контракты. Также с возрастом игроки становятся медленными, что больнее всего бьет по защитникам, которым все сложнее справляться с юркими нападающими.
ax = plt.subplot(111)
kmf.fit(df.career_length[df.Position == 'D'], event_observed=df.observed[df.Position == 'D'],
label="Defencemen")
kmf.plot(ax=ax, ci_force_lines=True)
kmf.fit(df.career_length[df.Position == 'F'], event_observed=df.observed[df.Position == 'F'],
label="Forwards")
kmf.plot(ax=ax, ci_force_lines=True)
plt.ylim(0,1);Похоже, что продолжительность карьеры защитников чуть короче, чем у нападающих. Чтобы удостовериться в верности вывода проведем статистический тест на основе критерия хи-квадрат:
from lifelines.statistics import logrank_test
dem = (df["Position"] == "F")
L = df.career_length
O = df.observed
results = logrank_test(L[dem], L[~dem], O[dem], O[~dem], alpha=.90 )
results.print_summary()Results
t 0: -1
test: logrank
alpha: 0.9
null distribution: chi squared
df: 1
__ p-value ___|__ test statistic __|____ test result ____|__ is significant __
0.05006 | 3.840 | Reject Null | True Итак, на 10% уровне значимости отвергаем нулевую гипотезу: защитники действительно имеют больший шанс завершить карьеру раньше, чем нападающие, при этом, как видно по графику, ближе к концу карьеры разница увеличивается, что также подтверждает выдвинутый ранее тезис: старый защитник все меньше успевает за игрой и становится все менее востребован.
Регрессия выживаемости
Зачастую у нас также имеются и другие факторы, влияющие на продолжительность «жизни», которые мы бы хотели учесть. Для этого была разработана модель регрессии выживаемости, которая, как и классическая линейная регрессия имеет зависимую переменную и набор факторов.
Рассмотрим один из популярных подходов к оценке параметров регрессии — аддитивную модель Аалена, который в качестве зависимой переменной выбрал не сами временные интервалы, а рассчитанные на их основе значения функции угрозы :
Перейдем к реализации модели. В качестве факторов модели примем количество очков, позицию игрока, дату начала карьеры и общую полезность команде (±):
from lifelines import AalenAdditiveFitter
import patsy # используем библиотеку patsy, чтобы создать design матрицу из факторов
# -1 добавляет столбец из единиц к матрице, чтобы обучить константу модели
X = patsy.dmatrix('Position + Points + career_start + Balance -1', df, return_type='dataframe')
aaf = AalenAdditiveFitter(coef_penalizer=1.0, fit_intercept=True) # добавляем penalizer, который делает регрессию более стабильной, в случае мультиколлинеарности или малой выборки)
Теперь, когда все готово, обучим регрессию выживаемости:
X['L'] = df['career_length']
X['O'] = df['observed'] # добавляем career_length и observed к матрице факторов
aaf.fit(X, 'L', event_col='O')Попробуем оценить, сколько еще сезонов отыграют в НХЛ 2 игрока: Дерек Степан, нападающий, который начал свою карьеру в 2010 году и набрал 310 очков с показателем полезности +109 и сравним его с менее успешным игроком НХЛ — Класом Дальбеком, который попал в НХЛ в 2014 году, набрал 11 очков с показателем полезности -12.
ix1 = (df['Position'] == 'F') & (df['Points'] == 360) & (df['career_start'] == 2010) & (df['Balance'] == +109)
ix2 = (df['Position'] == 'D') & (df['Points'] == 11) & (df['career_start'] == 2014) & (df['Balance'] == -12)
stepan = X.ix[ix1]
dahlbeck = X.ix[ix2]
ax = plt.subplot(2,1,1)
aaf.predict_cumulative_hazard(oshie).plot(ax=ax)
aaf.predict_cumulative_hazard(jones).plot(ax=ax)
plt.legend(['Stepan', 'Dahlbeck'])
plt.title('Функция угрозы')
ax = plt.subplot(2,1,2)
aaf.predict_survival_function(oshie).plot(ax=ax);
aaf.predict_survival_function(jones).plot(ax=ax);
plt.legend(['Stepan', 'Dahlbeck']);Как и ожидалось, у более успешного игрока ожидаемая продолжительность карьеры выше. Так, у Степана вероятность сыграть больше 11 сезонов — 80%, в то время как у Дальбека — всего 55%. Также по кривой угрозы видно, что начиная с 13 сезона резко возрастает риск завершить карьеру на следующий сезон, причем у Дальбека он растет быстрее, чем у Степана.
Кросс-валидация
Чтобы более строго оценить качество регрессии используем встроенную в библиотеку lifelines процедуру кросс-валидации. При этом, работая с цензурированными данными, мы не можем использовать в качестве метрики качества среднеквадратическую ошибку и подобные критерии, поэтому в библиотеки используется concordance index или индекс согласия, который является обобщением AUC-метрики. Проведем 5-шаговую кросс-валидацию:
from lifelines.utils import k_fold_cross_validation
score = k_fold_cross_validation(aaf, X, 'L', event_col='O', k=5)
print (np.mean(score))
print (np.std(score))Out:0.764216775131
0.0269169670161
Средняя точность по всем итерациям равна 76,4% с отклонением в 2,7%, что говорит о достаточно неплохом качестве алгоритма.
Ссылки
- Документация библиотеки lifelines
- J.Klein, M.Moeschberger. Survival Analysis. Techniques for censored and truncated data — книга с множеством примеров и датасетов, доступ к которым можно получить через пакет KMsurv в R.
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |






