И в теории, и в эксперименте треугольник Р1 Р2 Р3 является той поверхностью, на которой не появляются цвета (белый треугольник за призмой - примеч.перев.). Если мы поставим в точку Р3 контрольный экран, то тогда, начиная с этой точки на экране первый раз появится непрерывная окрашенная полоса (до точки Р3 цветная полоса разрывалась белой зоной - примеч. перев.). Эта цветная полоса не содержит зеленого цвета.
Для нашей экспериментальной проверки мы выбираем щель бленды шириной 1 см. Это означает, что появление сплошной окрашенной полосы (зоны) на расстоянии 61см за призмой было бы подтверждением теории школьной физики. Если же, напротив, появление сплошной окрашенной полосы произойдет только на расстоянии 121см, то это служило бы подтверждением гетеанистической теории.
Измерения расстояния Р2Р3 в эксперименте при ширине щели в 1 см дают расстояние в 115см. Следовательно, подтверждаются тезисы гетеанизма. Расхождение между расчетной и экспериментальной величиной должно быть точно описано при анализе погрешностей, допущенных при измерении.
Здесь мы могли бы констатировать, что результаты, полученные в эксперименте, подтверждают точку зрения Гёте.
7. Выводы по результатам проведенных экспериментов
В начале нашей работы мы показали, что появление зеленого цвета в дисперсионном спектре по разному объясняется с точки зрения школьной физики и с точки зрения гетеанизма. Мы называли это распутьем, перекрестком научных путей. Конкретные исследования подтвердили, что именно гетеанистические тезисы по поводу возникновения зеленого цвета в спектре соответствуют реальному положению вещей. Этот результат имеет исключительную важность.
Вначале мы утверждали, что для появления зеленого цвета (по Гёте) необходимо, чтобы коэффициент преломления для желтого был больше, чем коэффициент преломления для синего. По результатам экспериментов можно сделать конкретные выводы о соотношении коэффициентов преломления n:
nкрасный = nголубой
и
nжелтый = nфиолетовый
Итак, изменения коэффициента преломления в дисперсионном спектра происходит не непрерывно от красного к фиолетовому. Между желтым и голубым имеется скачок, причем в соответствие с теорией гетеанизма коэффициент преломления для зеленого вообще невозможно определить!
Как теоретические выкладки, так и экспериментальные результаты наглядно подтверждают тезисы гетеанизма. Они не дают никаких оснований для компромисов между противоположными теориями школьной физики и гетеанизма.
Результат наших исследований, проведенных до сих пор, непосредственно побуждает нас к дальнейшим действиям. Они могут быть направлены на разрешение следующих принципиальных вопросов:
- является ли зеленый в дисперсионном спектре квазимонохромным или это смешанный цвет?
- являются ли образующиеся в точках Р1 и Р2 краевые спектры спектрально чистыми, начиная с места их возникновения?
- содержатся ли спектральные цвета в белом свете хотя бы потенциально?
- может ли непрерывная спектральная полоса - при использовании в экспериментах параллельного света - появиться
исключительно в одном, заранее определенном месте?
- могут ли быть технически использованы результаты, достигнутые в соответствие с теорией гетеанизма?
Ответы на эти вопросы наверняка могли бы быть очень интересны при сравнительной оценке гетеанизма и школьной физики. Однако в рамках этой работы такое сравнение не представляется возможным. Тем не менее один из вышеназванных вопросов мы хотели бы рассмотреть боле подробно. Другие вопросы мы при дальнейшем изложении можем рассмотреть лишь с принципиальной стороны.
Читатель, желающий поближе ознакомиться с проблемами гетеанизма, мог бы запросить у автора до сих пор неопубликованные работы по заданным вопросам и другим базисным проблемам.
Наше проведенное до сих пор рассмотрение ограничивалось описанием и интерпретацией явлений, связанных с возникновением зеленого в дисперсионном спектре. До сих пор мы оставляли без внимания вынесенное в заголовок работы утверждение, что зеленый цвет представляет собой некое распутье, размежевание теорий. Прежде чем определить нашу позицию по этому поводу, нам хотелось бы еще раз более детально рассмотреть этот вопрос.
автор Natalie в Вс Апр 17, 2011 12:46 am
Описывая проблему, мы указывали на то, что в соответствие с теорией гетеанизма зеленый не может содержаться в белом свете. Но это значит, что появление зеленого в эксперименте не следует считать наружным выявлением того, что уже содержалось в свете, нет, здесь зеленый создается заново, продуцируется заново. В проводимых до сих пор исследованиях мы показали, что тезисы гетеанизма относительно положения точки Р3 находятся в полном согласии с результатами эксперимента. Повторим, что же это означает в смысле гетеанизма:
Там, где в дисперсионном спектре желтый и голубой накладываются друг на друга, возникает в качестве спектрального цвета зеленый. Возникновение зеленого предполагает, что коэффициент преломления для желтого больше, чем коэффициент преломления для синего.
Зеленый не содержится в белом свете, но продуцируется, создается заново.
Кроме того, на основании результатов нашего расчета и экспериментальной проверки мы можем сделать вывод относительно коэффициентов преломления в дисперсионном спектре; имеет место следующее:
nкрасный = nголубой
nжелтый = nфиолетовый
Этот вывод так необычен, что нам хотелось бы подкрепить его еще одним экспериментом, в основу которого положен рис.5
Рис.5 Дисперсионный спектр по Гёте на заслонке
В нашем модифицированном оборудовании для эксперимента мы заменяем бленду со щелью заслонкой, имеющей точно такую же ширину, какую имела до сих пор используемая щель на бленде. Здесь мы тоже рассчитываем по Гёте местоположение точки Р3 , где впервые должна появиться непрерывная цветовая полоса. Последовательность цветов в этом случае будет уже не красный-оранжеый-желтый-голубой-синий-фиолетовый, но голубой-синий-фиолетовый-красный-оранжевый-желтый. Там, где в опыте со щелью при наложении желтого и синего появлялся зеленый, теперь, при новых условиях опыта при наложении фиолетового и красного становится видимым цвет, который до сих пор еще не появлялся - пурпурный.
В случае правильности утверждения гетеанизма о том, что краевые спектры по своей геометрии полностью конгруэнтны, равны между собой, точка Р3 в модифицированных условиях опыта должна появиться в том же самом месте, как и прежде, то есть при расчете для обычного спектра. [N - Конгруэнция лучей - это такая совокупность линий в пространстве, для которой выполняется условие, что через любую точку пространства можно провести только одну линию из этой системы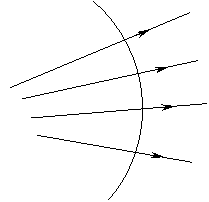 
ссылка ]
Эксперимент подтверждает это предположение! Сведения о том, что краевые спектры конгруэнтны по своей геометрии имеет весьма перспективные следствия; мы хотим подкрепить эти сведения результатами экспериментов других гетеанистов.
Группа норвежских гетеанистов (имеются в виду проводимые в пятидесятые годы 20 века исследования Андре Бьерке и его группы - примеч. перев.) написала тексты, по смыслу прямо противоположные теоремам и экспериментам Ньютона, приведенным в его книге "Оптика". Высказывания, полярно противоположные тем, что приведены в книге, были подтверждены экспериментально. Результаты своих исследований норвежские ученые обнародовали в одной полезной для чтения книге ( 2* ) В качестве примера мы хотим привести здесь вторую теорему Ньютона:
"Солнечный свет состоит из лучей с разными коэффициентами преломления".
Противоположный текст гласит:
"Тьма состоит из лучей с различными коэффициентами преломления".
Правильность утверждения в противоположном тексте мы уже показали в эксперименте, изображенном на рис.5
Сведения, приобретенные нами до сих пор дают нам право на вопрос: Если зеленый в спектре является продуцированным, своего рода продуктом, то как обстоит в этом смысле дело с другими спектральными цветами? Этот вопрос носит центральный характер и требует тщательного исследования. Чтобы не расширять чрезмерно объем настоящей работы, мы хотим с помощью трех экспериментов найти ответ, который мог бы стать удовлетворительным.
Мы начинаем с эксперимента, изображенного на рис.6 
Рис.6 Возникновение цветов от спектрального цвета
Прежде всего получим один спектр в соответствие с рис.3. При использовании призмы изготовленной из стекла сорта БК7 и ширине щели бленды b=1см, в соответствие с расчетом, произведенным в главе 4, мы получим на экране, расположенном на расстоянии около 120см от призмы, непрерывный спектр размером около 2см. В соответствие с рис.6 одну часть спектральной полосы через щель, проделанную в самом экране мы спроектируем на второй экран. Так первый экран будет выполнять функции второй бленды. По теории школьной физики, на втором экране можно увидеть те же спектральные цвета, которые оказались на первом экране (точнее, в том месте первого экрана, где была вырезана щель -примеч. перев.) Но, к нашему удивлению, здесь снова образуются два уже известных нам краевых спектра, и на соответствующем расстоянии мы получаем непрерывный спектр с зеленой зоной в центре. Снова в соответствие с нашим прежним расчетом возникает новый спектр, причем, если ширина щели в первом экране составляет 3мм, спектр будет расположен на расстоянии 35см от первого экрана.
Уже описанная нами функциональная связь ширины щели и расстояния до точки Р3 сохраняется в новой ситуации. Появление нового спектра при этом не зависит от того, в каком месте первой спектральной полосы часть этой цветной полосы мы пропустим сквозь первый экран.
Очевидно, что в каждой из этих ситуаций спектральные цвета возникают заново.
Особенно впечатляющим становятся эти явления, если мы немного модифицируем опыт. В этом случае мы пропускаем через первый экран очень узкий спектр центральной полосы. Непосредственно за экраном цветной свет попадает на дифракционную решетку, линии которой устанавливаются параллельно щели в экране. При любом положении щели мы получаем непрерывный дифракционный спектр. На дифракционной решетке спектральные цвета тоже, совершенно очевидно, возникают заново.
В следующем варианте этого эксперимента мы уже не пропускаем сквозь первый экран узкий сектор спектральных цветов, но поворачиваем щель на 90 градусов и пропускаем сквозь первый экран узкий вырез по всему спектру, чтобы он падал на дифракционную решетку, тоже повернутую на 90 град. См. схему :
Вопреки любой из известных теорий, на проходе появляется дифракционный спектр, повернутый на 90 град. по отношению к выходному спектру (то есть той части первого спектра на первом экране, которая была пропущена сквозь экран). Формат этой работы был бы излишне расширен, если бы мы стали подробно обсуждать эти явления.
В следующем эксперименте мы хотим показать, как явления свидетельствуют о том, что спектральные цвета не содержатся в белом цвете, но все снова и снова заново порождаются в каждом эксперименте. Для дальнейшего исследования вышеназванной проблематики мы приводим опыт , изображенный на рис.7
Рис.7 Появление цветов в случае полного внутреннего отражения .
К - временно вдвигаемый контрольный экран;
α1 - предельный угол полного внутреннего отражения;
краевые спектры, возникающие в призме, не показаны
Предлагаемый для обсуждения эксперимент является модификацией девятого опыта Ньютона. На отражательную призму падает под углом β пучок параллельного света, так что отражение происходит в области предельного угла полного внутреннего отражения α 1 . Исходя из положения школьной физики, гласящем, что красный преломляется сильнее, чем фиолетовый и, соответственно, коэффициент преломления для линии С' меньше, чем коэффициент преломления для линии h , в случае предельного угла полного внутреннего отражения должно было бы произойти следующее: фиолетовый еще отражается призмой, тогда как красный уже оставляет призму и выходит наружу. Наш опыт мы построили так, что красный и оранжевый становятся видимы на экране 1; в то время как остаток светового пучка отражается в призме и выходит из призмы 1 в точках С и С1. Этот остаток светового пучка мы направляем на вторую отражательную призму, причем так, что процесс, имевший место в призме 1 повторяется. Если в нашем распоряжении имеется достаточно сильный источник света, мы можем повторить этот процесс и в третий, и в четвертый раз. В каждом случае мы исключаем из светового пучка красный и оранжевый. Лишь оставшуюся часть светового пучка пропускаем мы, как и в предшествующих опытах, через призму. Если бы теория школьной физики была верна, то после многих проходов через отражательную призму, при каждом из которых красный удаляется из светового пучка, при завершающем проходе через призму (уже не отражающую, а преломляющую) в свете не должно было бы содержаться красного. Для школьной физики остается необъяснимым, а для гетеанизма - вполне ожидаемым и предсказуемым - появление за последней призмой ( в нашем случае на экране 3 ) сплошного спектра с красной составляющей, итак, все того же самого спектра, который не отличается от других спектров. Совершенно очевидно, что красный все снова и снова рождается заново.
Но не только появление красного противоречит здесь положениям школьной физики. Та часть светового пучка, которая отразилась в первой призме, должна была бы произвести цвет, дополнительный к красному. Свет, выходящий из первой призмы между точками С и С1, должен быть окрашен в голубой цвет. Вдвинув в это место контрольный экран К, мы увидим, что остаток пучка остался чисто белым. Явления на контрольном экране, помещенном за другой отражательной призмой, тоже в результате не показывают никакой окраски остаточного пучка.
Самым убедительным образом опыт подтверждает точку зрения гетеанизма о том, что спектральные цвета продуцируются, а не содержатся заранее – пусть даже потенциально - в белом свете.
Из множества дальнейших экспериментов в связи с поставленным вопросом мы хотим подробнее коснуться третьего примера. Основой для дискуссии является здесь опыт, построенный по рис.8
Рис 8. Появление цветов при опыте с двумя призмами в различных положениях.
Исходная ситуация состоит в том, что мы снова создаем дисперсионный спектр по рис.3. В том месте, где уже появился сплошной спектр, мы добавляем одну часть бленды, перекрывающей цвета от красного до зеленого. На место второй части бленды мы ставим на пути лучей вторую призму, причем так, чтобы вершина призмы и нижний край бленды образовали щель шириной около 3 мм.
На экране, помещенном за построенной таким образом щелью, мы можем наблюдать следующие явления: За щелью снова образуется уже ожидаемый сплошной спектр с зеленым в центре. Кроме того, часть спектральной полосы, проходящая сквозь вторую призму, способствует возникновению следующей спектральной полосы. В ней несомненно образуется и красный и зеленый, несмотря на то, что эти цветовые части были экранированы посредством верхней бленды и не должны были бы содержаться в остатке. Тут мы имеем новое экспериментальное доказательство верности тезиса гетеанизма, гласящего, что спектральные цвета каждый раз возникают заново.
Читателю, заинтересованному этим вопросом, мы сообщаем, что вариации опытов с двумя или несколькими призмами, расположенными в других местах дают ошеломляющие результаты, и все они подтверждают, что цвета не могут содержаться в белом свете. Для практического воспроизведения опыта мы хотели бы указать, что всегда в случае пропускания света сквозь щель, возникновение цветов выглядит особенно впечатляюще, если проходящий сквозь щель пучок света падает на дифракционную решетку. В качестве добавления к имеющемуся положению вещей мы должны указать и на следующее: на спектры, возникающие в цветном свете, в любом случае оказывает влияние тот цвет, который пропускается сквозь экран. Это происходит в соответствие с закономерностью взаимодействия дополнительных цветов, которую мы здесь хотим рассмотреть подробно. Принимая во внимание эту закономерность, мы во всех случаях найдем подтверждение нашему основному тезису.
После того как мы занимались до сих пор теоретической и практической стороной эксперимента, чтобы проверить, насколько соответствуют действительности кажущиеся столь необычными тезисы гетеанизма, мы хотим заняться столь же важным вопросом: в какой степени зеленый цвет в дисперсионном спектре может считаться "перекрестком естественнонаучных путей"?
