Мне попалась интересная задача.

Задача. Определите при каких значениях параметра а уравнение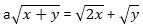 имеет единственное решение.
Решение. Понятно, что пара (0; 0) является решением данного уравнения при любом значении параметра а. Теперь нашу задачу можно переформулировать иначе.

При каких значениях параметра а уравнение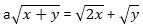 не имеет решений отличных от (0; 0).

Так как (x; y) отлично от (0; 0), то данное уравнение можно преобразовать к виду и нужно определить при каких значениях параметра а это уравнение не имеет решений.

Здесь есть прямой путь - использовать знание из теории функций с несколькими переменными и определить множество значений функции, расположенное в правой части последнего уравнения. но этот естественный путь для школьника не доступен. Однако рассказать ему об этом нужно.

Школьному учителю в данной ситуации остается только придумывать неестественные пути решения этой задачи. Например, такой способ.

Пусть , тогда , где 0 ≤ t ≤ 1 и получим уравнение . Это уравнение не имеет решений тогда и только тогда, когда а не принадлежит множествк значений функции из правой части уравнения.

Искомое множество значений функции находим методами теории функции одной переменной и получаем а ∈ (-∞ 1) ∪ (√3; +∞).

Задача для самостоятельного решения,/b>

Определите при каких значениях параметра а уравнение имеет единственное решение.