Сначала несколько слов об этой олимпиаде.

Всесибирская физико-математическая олимпиада школьников была организована в 1962 году по инициативе академика М.А. Лаврентьева.
Особенностью олимпиады является также то, что призеры олимпиады приглашаются в Летнюю физико-математическую школу, проводимую в Академгородке (г.Новосибирск), по результатам обучения в которой старшеклассники принимаются в физико-математическую школу, ныне Специализированный учебно-научный центр Новосибирского государственного университета.

По Решению Российского совета олимпиад школьников Всесибирская открытая олимпиада школьников включена в Перечень олимпиад школьников на 2010/2011 год по математике (2 уровень), физике(2 уровень), химии(3 уровень), биологии (3 уровень) и информатике (2 уровень). Это означает, что победители и призеры олимпиад имеют право на получение одной из следующих льгот при поступлении в вузы РФ:

быть приравненными к лицам, набравшим максимальное количество баллов по ЕГЭ по соответствующему предмету;
быть приравненными к лицам, успешно прошедшим дополнительные вступительные испытания;
быть зачисленными в образовательное учреждение без вступительных испытаний.

А теперь о задаче.

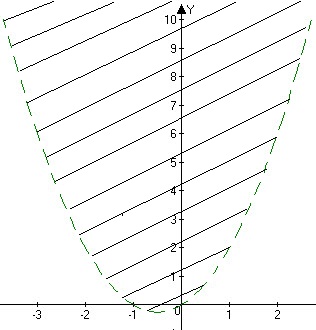
Найти все точки (х; y) координатной плоскости, через которые не проходит ни одна прямая семейства y = (2px + 1)x - p².

Решение. Пусть через точку (х; y) не проходит ни одна прямая из указанного семейства. Это означает, что уравнение y = (2px + 1)x - p² не имеет решений относительно р.

Уравнение y = (2px + 1)x - p² запишем как квадратное относительно р: p² - 2хр + y - x = 0.

Так как последнее уравнение не имеет решений относительно р, то его дискриминант равен нулю, т. е. D = x² - y + x < 0, y > x² + x .

Значит, условию задачи удовлетворяют все точки (х; y), для которых y >x² + x . Эти точки изображены на следующем рисунке.