-Рубрики
- 01 ЖИРНОСТЬ (317)
- ФОТОГРАФИЯ (48)
- Бабочки (1)
- кошки (60)
- Природа! (49)
- подводный мир (4)
- приколы с ..... (20)
- прочии (73)
- птицы (20)
- 006 Значение учение ВИКИПЕДИЯ (260)
- 001 Кулинарно (3)
- 02 Мифы и Легенды (50)
- -- боги --- (12)
- 03 ????? АААА ?????? (1566)
- Поэзия (551)
- СТИХИ (260)
- 04 ТРАНСПОРТ (212)
- 01.......авто экзотика (115)
- 06,,,,,,ПРОЧИЕ (32)
- 02........мото экзотика (24)
- 03........трицикл (8)
- 04 Машино-техника (17)
- 05 Велосипеды (19)
- 05 Биография Людей "" Х "" (306)
- Актёры и танцоры (42)
- военные .... (4)
- музыканты и певцы и дирижёры и т.д. (56)
- наше время (10)
- Политики и юристы (3)
- правители истории (2)
- Прочее (10)
- прошлое (24)
- Учёные и писатели и философ и теоретик (85)
- художники (16)
- 06 В-112 (1986)
- 01 Дневники (1386)
- ПОСВЯЩАЕТСЯ ДНЮ ПОБЕДЫ! (26)
- Про работу (1)
- 03 Без слов! (206)
- 05 Посты (75)
- 06 Что, где, как да? (32)
- 07 Новости или Чепуха или Мысли вслух (26)
- 08 Ведро с мусором (26)
- 09 ЧАС......... (9)
- 10 Прочие (69)
- 11 Пузыри.... (7)
- 12 Крушение (5)
- 13 Гони Инспектору Бабки и Двигай Дальше!! (17)
- 14 Про фильмы (67)
- 15 Комп - планшет и тд (4)
- 16 Знаки и Символы (2)
- 17 Слухи и сплетни (3)
- 18 Дням посвящается............ (10)
- 19 Знаменательные события (2)
- 07 ДЕТИ (117)
- для детей (92)
- прочие (13)
- 08 ЕДА! как прочитать об том как готовить (465)
- ТО ЧТО ОВОЩИ И ФРУКТЫ !! (3)
- 09 ЗВУЧАНИЕ***** (535)
- Адская белочка (3)
- аудио (215)
- видео (299)
- тексты песен (15)
- ядерная война (2)
- 10 ИСКУССТВО 2 (5949)
- 01 Фотограф (209)
- 04 ЯННА_КОТ (20)
- 12 Календарики (9)
- -- Viktoria_Krass -- (4)
- 08 Анимация (2)
- ФАНТАЗИЯ (1)
- 17 Мозаика (1)
- 01 Художники (4004)
- 02 Живопись (309)
- 03 Прочие (187)
- ---- САБРИНА ---- (28)
- 04 Фотографии (280)
- 04 Фентези (58)
- 05 Натюрморты (77)
- 06 Акварельки (97)
- 07 Памятник — скульптура (54)
- 08 Разно вольные рамки.. (16)
- 09 Иллюстратор (281)
- 10 Куклы (138)
- 11 Пейзажи (27)
- 12 Карикатуры (21)
- 13 Фарфор (61)
- 14 Бронза - Серебро (16)
- 15 Стеклянный мир (5)
- 16 Рисунок (34)
- 17 Резьба (11)
- 18 Гравюры (1)
- Просто приятное !! (58)
- 19 Татуировки (3)
- 20 Фигурки .. (1)
- 21 Сундучки -- Ларцы (2)
- 22 Шкатулки - коробочки (2)
- 23 еЁ РАБОТЫ (21)
- 25 Оружие (2)
- 26_Картинки (63)
- 27 Витражи (4)
- 28 Графика (2)
- 11 МИСТИКА (5)
- карты (1)
- 12 МИХАИЛ ЗАДОРНОВ (7)
- Записки Михаила Задорного (5)
- 13 МОДА ВСЕГДА ****? (95)
- РУКАДЕЛИЕ (40)
- Разное (9)
- 14 МУЛЬТ ЧТО ТО (5)
- 15 НАРОДНАЯ МЕДИЦИНА (10)
- 16 ШЕДЕВРЫ ЛИТЕРАТУРЫ (1447)
- 001 Цитаты из книг и ... (930)
- 006 Записки успешного человека (112)
- 002 Цитатные посты (132)
- 003 Прочие (127)
- 004 Черныши (10)
- 005 ЛЮДИ ИСТОРИИ (84)
- 17 ПО МИРУ! (296)
- города (44)
- МУЗЕИ (1)
- * ВОДА * (1)
- Аквопарк (1)
- ГОРЫ (1)
- дворцы (9)
- дома (27)
- замки (43)
- ЗВЕЗДЫ МИРА (1)
- КОРАБЛИКИ (1)
- мосты (15)
- отели (16)
- парки (9)
- призраки (1)
- прочие (39)
- руины (2)
- Соборы (2)
- сады (19)
- страны (20)
- усадьбы (3)
- церкви - храмы (37)
- чудеса света (6)
- 18 ПОЛЕЗНАЯ ИНФОРМАЦИЯ ДЛЯ (161)
- ДЛЯ РЕМОНТОВ и СТРОИТЕЛЬСТВА (84)
- Красота е.. (6)
- ОБУВИ (1)
- утварь для дома и ........ (44)
- 20 ИСТОРИЯ (3)
- Агата Кристи (1)
- 21 РАЗНЫЕ КНИГИ (67)
- Николай Задорнов (1)
- Прочие (10)
- 22 ЮВЕЛИРТОРГ ИЛИ КРАСИВОЕ НО ДОСТУПНОЕ! (75)
- безделушки знаменитых людей (6)
- ПРОЧИЕ (26)
- 19 ЮМОР ИЛИ @@@@@ (33)
- Юмор -Юмор в картинках. (5)
- 24 РЕЛИГИЯ ! (87)
- Молитва (59)
- Пророчества (2)
- Святые мученики (4)
-Помощь новичкам
Проверено анкет за неделю: 0
За неделю набрано баллов: 0 (85597 место)
За все время набрано баллов: 29 (20558 место)
-Музыка
- Максим Леонидов - Аптекарь, Судья, Бобер и Сова
- Слушали: 40 Комментарии: 1
- 05 - Михаил Задорнов - Жизнь В Америке.mp3
- Слушали: 140 Комментарии: 0
- 06 - Михаил Задорнов - За Рубежом[1]....mp3
- Слушали: 29 Комментарии: 0
- 03 - Михаил Задорнов - Буду Сказать Без Бумажки.mp3
- Слушали: 32 Комментарии: 0
- 02 - Михаил Задорнов - Бестолковый Словарь.mp3
- Слушали: 42 Комментарии: 0
-Поиск по дневнику
-Подписка по e-mail
-Друзья
-Постоянные читатели
-Сообщества
-Трансляции
-Статистика
Записей: 14231
Комментариев: 4520
Написано: 24624
Теорема Гёделя о неполноте |
Теорема Гёделя о неполноте
Теоре́ма Гёделя о неполноте́ и втора́я теоре́ма Гёделя[~ 1] — две теоремы математической логики о принципиальных ограничениях формальной арифметики и, как следствие, всякой формальной системы, в которой можно определить основные арифметические понятия: натуральные числа, 0, 1, сложение и умножение.
Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.
Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой арифметики.
Эти теоремы были доказаны Куртом Гёделем в 1930 году (опубликованы в 1931) и имеют непосредственное отношение ко второй проблеме из знаменитого списка Гильберта.
Содержание
[убрать]
Теорема Гёделя о неполноте[править | править вики-текст]
В первоначальной форме[править | править вики-текст]
В своей формулировке теоремы о неполноте Гёдель использовал понятие ω-непротиворечивой формальной системы — более сильное условие, чем просто непротиворечивость. Формальная система называется ω-непротиворечивой, если для всякой формулы A(x) этой системы невозможно одновременно вывести формулы А(0),А(1), А(2), … и ∃x ¬A(x) (другими словами, из того, что для каждого натурального числа n выводима формула A(n), следует невыводимость формулы ∃x ¬A(x)). Легко показать, что ω-непротиворечивость влечёт простую непротиворечивость (то есть, любая ω-непротиворечивая формальная система непротиворечива)[6].
В процессе доказательства теоремы строится такая формула A арифметической формальной системы S, что[6]:
- Если формальная система S непротиворечива, то формула A невыводима в S; если система S ω-непротиворечива, то формула ¬A невыводима в S. Таким образом, если система S ω-непротиворечива, то она неполна[~ 2] и A служит примером неразрешимой формулы.
Формулу A иногда называют гёделевой неразрешимой формулой[7].
Интерпретация неразрешимой формулы[править | править вики-текст]
В стандартной интерпретации[~ 3] формула A означает «не существует вывода формулы A», то есть утверждает свою собственную невыводимость в S. Следовательно, по теореме Гёделя, если только система S непротиворечива, то эта формула и в самом деле невыводима в S и потому истинна в стандартной интерпретации. Таким образом, для натуральных чисел формула A верна, но в S невыводима[8].
В форме Россера[править | править вики-текст]
В процессе доказательства теоремы строится такая формула B арифметической формальной системы S, что[9]:
- Если формальная система S непротиворечива, то в ней невыводимы обе формулы B и ¬B; иначе говоря, если система S непротиворечива, то она неполна[~ 2], и B служит примером неразрешимой формулы.
Формулу B иногда называют россеровой неразрешимой формулой[10]. Эта формула немного сложнее гёделевой.
Интерпретация неразрешимой формулы[править | править вики-текст]
В стандартной интерпретации[~ 3] формула B означает «если существует вывод формулы B, то существует вывод формулы ¬B». Согласно же теореме Гёделя в форме Россера, если формальная система S непротиворечива, то формула B в ней невыводима; поэтому, если система S непротиворечива, то формула B верна в стандартной интерпретации[11].
Обобщённые формулировки[править | править вики-текст]
Доказательство теоремы Гёделя обычно проводят для конкретной формальной системы (не обязательно одной и той же), соответственно утверждение теоремы оказывается доказанным только для одной этой системы. Исследование достаточных условий, которым должна удовлетворять формальная система для того, чтобы можно было провести доказательство её неполноты, приводит к обобщениям теоремы на широкий класс формальных систем. Пример обобщённой формулировки[12]:
- Всякая достаточно сильная рекурсивно аксиоматизируемая непротиворечивая теория первого порядка неполна.
В частности, теорема Гёделя справедлива для каждого непротиворечивого конечно аксиоматизируемого расширения арифметической формальной системы S.
Полиномиальная форма[править | править вики-текст]
После того, как Юрий Матиясевич доказал диофантовость любого эффективно перечислимого множества и были найдены примеры универсальных диофантовых уравнений, появилась возможность сформулировать теорему о неполноте в полиномиальной (или диофантовой) форме[13][14][15][16]:
-
Для каждой непротиворечивой теории T можно указать такое целое значение параметра K, что уравнение
-
- не имеет решений в неотрицательных целых числах, но этот факт не может быть доказан в теории T. Более того, для каждой непротиворечивой теории множество значений параметра K, обладающих таким свойством, бесконечно и алгоритмически неперечислимо.
Степень данного уравнения может быть понижена до 4 ценой увеличения количества переменных.
Набросок доказательства[править | править вики-текст]
В своей статье Гёдель даёт набросок основных идей доказательства[17], который приведён ниже с незначительными изменениями.
Каждому примитивному символу, выражению и последовательности выражений некоторой формальной системы[~ 4]S поставим в соответствие определённое натуральное число[~ 5]. Математические понятия и утверждения таким образом становятся понятиями и утверждениями о натуральных числах, и, следовательно, сами могут быть выражены в символизме системы S. Можно показать, в частности, что понятия «формула», «вывод», «выводимая формула» определимы внутри системы S, то есть можно восстановить, например, формулу F(v) в S с одной свободной натурально-числовой переменной v такую, что F(v), в интуитивной интерпретации, означает: v — выводимая формула. Теперь построим неразрешимое предложение системы S, то есть предложение A, для которого ни A, ни не-A невыводимы, следующим образом:
Формулу в S с точно одной свободной натурально-числовой переменной назовём класс-выражением. Упорядочим класс-выражения в последовательность каким-либо образом, обозначим n-е через R(n), и заметим, что понятие «класс-выражение», также как и отношение упорядочения R можно определить в системе S. Пусть α — произвольное класс-выражение; через [α;n] обозначим формулу, которая образуется из класс-выражения α заменой свободной переменной на символ натурального числа n. Тернарное отношение x = [y;z] тоже оказывается определимым в S. Теперь определим класс K натуральных чисел следующим образом:
- n∈K ≡ ¬Bew[R(n);n] (*)
(где Bew x означает: x — выводимая формула[~ 6]). Так как все определяющие понятия из этого определения можно выразить в S, то это же верно и для понятия K, которое из них построено, то есть имеется такое класс-выражениеC, что формула [C;n], интуитивно интерпретируемая, обозначает, что натуральное число n принадлежит K. Как класс-выражение, C идентично некоторому определённому R(q) в нашей нумерации, то есть
C = R(q)
выполняется для некоторого определённого натурального числа q. Теперь покажем, что предложение [R(q);q] неразрешимо в S. Так, если предложение [R(q);q] предполагается выводимым, тогда оно оказывается истинным, то есть, в соответствии со сказанным выше, q будет принадлежать K, то есть, в соответствии с (*), будет выполнено ¬Bew[R(q);q], что противоречит нашему предположению. С другой стороны, если предположить выводимым отрицание [R(q);q], то будет иметь место ¬q∈K, то есть Bew[R(q);q] будет истинным. Следовательно, [R(q);q] вместе со своим отрицанием будет выводимо, что снова невозможно.
Связь с парадоксами[править | править вики-текст]
В стандартной интерпретации[~ 3] гёделева неразрешимая формула A означает «не существует вывода формулыA», то есть утверждает свою собственную невыводимость в системе S. Таким образом, A является аналогомпарадокса лжеца. Рассуждения Гёделя в целом очень похожи на парадокс Ришара. Более того, для доказательства существования невыводимых утверждений может быть использован любой семантический парадокс[18].
Следует отметить, что выражаемое формулой A утверждение не содержит порочного круга, поскольку изначально утверждается только, что некоторая конкретная формула, явную запись которой получить несложно (хоть и громоздко), недоказуема. «Только впоследствии (и, так сказать, по воле случая) оказывается, что эта формула в точности та, которой выражено само это утверждение»[18].
Вторая теорема Гёделя[править | править вики-текст]
В формальной арифметике S можно построить такую формулу, которая в стандартной интерпретации[~ 3] является истинной в том и только в том случае, когда теория S непротиворечива. Для этой формулы справедливо утверждение второй теоремы Гёделя:
- Если формальная арифметика S непротиворечива, то в ней невыводима формула, содержательно утверждающая непротиворечивость S.
Иными словами, непротиворечивость формальной арифметики не может быть доказана средствами этой теории. Однако, могут существовать доказательства непротиворечивости формальной арифметики, использующие средства, невыразимые в ней.
Набросок доказательства[править | править вики-текст]
Сначала строится формула Con, содержательно выражающая невозможность вывода в теории S какой-либо формулы вместе с её отрицанием. Тогда утверждение первой теоремы Гёделя выражается формулой Con ⊃ G, гдеG — Гёделева неразрешимая формула. Все рассуждения для доказательства первой теоремы могут быть выражены и проведены средствами S, то есть в S выводима формула Con ⊃ G. Отсюда, если в S выводима Con, то в ней выводима и G. Однако, согласно первой теореме Гёделя, если S непротиворечива, то G в ней невыводима. Следовательно, если S непротиворечива, то в ней невыводима и формула Con.
Исторические сведения[править | править вики-текст]
23 октября 1930 года результаты Гёделя были представлены Венской академии наук Хансом Ханом. Основная статья была получена для публикации 17 ноября 1930 года и опубликована в начале 1931 года[19].
Примечания[править | править вики-текст]
|
ХУДОЖНИЦА БРОНВИН ХИЛЛ |
АВСТРАЛИЙСКАЯ ХУДОЖНИЦА. BRONWYN HILL




















|
---- С Масленицей !! ---- |
УРА !
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

|
100 книг по опросу |
|
Художник Дмитрий Михайлович Авласевич |
Художник Дмитрий Михайлович Авласевич
http://vdohnovenie2.ru/gorodskie-dozhdi-xudozhnik-d-m-avlasevich/











|
Процитировано 1 раз
Понравилось: 1 пользователю
35 лучших вдохновляющих книг |
|
Процитировано 2 раз
Понравилось: 2 пользователям
Геката |
| Геката | |
|---|---|
 Геката |
|
| Мифология: | Древнегреческая |
| В иных культурах: | Тривия |
| Дети: | 3 дочери от Гермеса |
| Иллюстрации на Викискладе? | |
Гека́та (др.-греч. Ἑκάτη) — древнегреческая богиня лунного света, преисподней и всего таинственного[1]. Она была также богиней ведьм, ядовитых растений, и многих других колдовских атрибутов. Геката была дочерью титана Перса (Perses), и ей по-прежнему поклоняются некоторые греческие политеисты. Возможно, само понятие сглаза пошло от неё, и святыни в её честь были возведены, чтобы умерить гнев злых демонов и духов в греческих мифах.[источник?]
Есть предположение, что культ Гекаты существовал сначала уфракийцев и от них уже перешёл к грекам.
В поэмах Гомера имя Гекаты не встречается; в «Теогонии» же Гесиодаона упоминается как дочь титана Перса[2] и Астерии; другие авторы называют её дочерью Зевса и Деметры или Зевса и Геры. Согласно Гесиоду, она получила свою долю власти ещё от титанов, Зевс оставил ей её[3].
По одной из версий, Гекатой стала похищенная Ифигения[4]. Ферекид называл её дочерью Аристея[5]. Гекатой иногда называют Артемиду[6].
У Диодора отец Гекаты отождествляется с братом Ээта, сыномГелиоса. По его изложению, она отравила своего отца Перса и стала царицей Тавриды. Вышла замуж за Ээта и родила Кирку, Медею иЭгиалея[7].
Орфей установил таинства Гекаты на Эгине, где её почитали больше всего[8]. Её храм был в Аргосе[9], таинства в честь Гекаты проводились в Зеринфе[10], где в её пещере приносили в жертву собак[11]. У Пиндара Геката именуется «обутою в красное»[12].
Ей посвящён I орфический гимн. Скульптор Алкамен впервые создал Гекату в виде трех соединённых статуй в Афинах[8]. Геката изображалась иногда в виде одной женской фигуры с двумя факелами в руках, иногда же в виде трёх связанных спинами фигур; этим как бы поясняется, что власть её распространялась на небо, землю и ад[источник не указан 1630 дней].
Геката дарует мудрость в народных собраниях, счастье на войне, богатую добычу на охоте и т. д. Как богиня преисподней, она считалась также богиней всего таинственного; греки представляли её себе порхающей с душами умерших на перекрестках. Поэтому культ Гекаты иногда связывают с перекрестками. Она помогает волшебницам, которые, как например Цирцея иМедея, учатся у неё своему искусству.
Геката родила Гермесу трех дочерей[13].
В некоторых источниках Кратейя (или Кратеида) как мать Скиллы либо именуется дочерью Гекаты, либо отождествляется с нею. Кратейя — это имя Ночной Гекаты[14]; либо имя Луны[15]. У Алексида была комедия «Кратейя, или Торговка снадобьями»[16].
В честь Гекаты назван астероид (100) Геката, открытый в 1868 году. В названии отражено и имя богини, и порядковый номер астероида, так как «гекатон» означает по-гречески сотню.
|
Сыктывкарская художница-кукольница |
|
Куклы-игрушки, как живые |
|
Понравилось: 1 пользователю
ЭТА КОШКА ПРЕДЛАГАЕТ ЗАЙТИ К НЕЙ |
|
|
Художник Джозеф Райт (Joseph Wright) - 1734 г - 1797 г. |
|
ХУДОЖНИК SIMONA JANKAUSKAITE \СИМОНА ЯНКАУСКАЙТЕ |
|
Процитировано 1 раз
Понравилось: 1 пользователю
Художник Анатолий Петкевич |
|
ОСЕНЬ |

Убегает осень по тропинкам,
как царевна в платье золотом.
Бледных туч заутренняя дымка
дождевым исстегана кнутом.
Облысели сонные долины.
пожелтели тихие луга.
У зарделись кудри у рябины,
как огни в унылых берегах...
Темный лес вздыхает виновато.
Осень правит девичьи дела:
примеряет бархатное злато
и смеется, глядя в зеркала.
Дышит небо призрачной тоскою.
Серебрятся ивы у пруда.
и листву, не знавшую покоя,
унесла журчащая вода...
Колдовством венчает листопады
до утра глазастая луна,
и земля, объятая прохладой,
красотою грустною полна...
Алена Васильченко

|
10 книг от депрессии |
|
Процитировано 5 раз
Понравилось: 2 пользователям
.. Стихи .. |
|
Понравилось: 2 пользователям
.. СТИХ .. |
А мужчины ведь тоже умеют любить...
И не спать по ночам и курить в нетерпенье,
И ворчать, придираясь опять к мелочам,
И рыдать перед кем-то, вставая с коленей.
А мужчины ведь тоже умеют любить...
Забывая себя и страдая от скуки,
И им также любимыми хочется быть,
В тишине целовать чьи-то нежные руки.
А мужчины ведь тоже умеют любить...
И мечтать в полутьме, улыбаясь незримо,
И наверное могут и верность хранить,
Для своей единственной милой.
А мужчины ведь тоже умеют любить...
Становясь на глазах, кто добрее, кто строже,
А мужчины ведь тоже умеют любить...
Как не каждая женщина сможет...
Мария Курзина
|
Понравилось: 1 пользователю
.. Стихи .. |
|
Понравилось: 1 пользователю
Художник Gordon King (114 работ) |
|
Мильва (наст. имя Мария Ильва Биолкати, итал. Maria Ilva |
Мильва
| Мильва | |||||
 Мильва |
|||||
| Основная информация | |||||
|---|---|---|---|---|---|
| Имя при рождении |
Maria Ilva Biolcati |
||||
| Дата рождения | |||||
| Место рождения | |||||
| Годы активности |
1959 — наст. время |
||||
| Страна | |||||
| Профессии | |||||
| Жанры | |||||
| Псевдонимы |
La Rossa, Grande Milva |
||||
| Награды |
|
||||
| milvalarossa.it | |||||
|
|
|||||
Мильва (наст. имя Мария Ильва Биолкати, итал. Maria Ilva Biolcati; род. 17 июля 1939 года, в Горо, провинция Феррара) — популярная итальянская певица, актриса и телевизионная ведущая.
Содержание
[убрать]
Биография[править | править вики-текст]
Она родилась в Горо, провинции Феррара в Италии.
В 1959 г. Мильва победила в конкурсе новых вокалистов и была названа абсолютной победительницей из более чем 7000 участников. В 1960 г. она записала свой первый 7" сингл с Cetra Records: песню «Milord» Эдит Пиаф. Её настоящий дебют состоялся в 1961 на сцене музыкального фестиваля в Сан-Ремо.
В 1965 знакомство с итальянским режиссёр Джорджо Стрелерпривело к изменениям в её карьере: Стрелер помог ей развить сценические навыки и петь в итальянских театрах (в особенности в Piccolo Teatro в Милане), и она начала исполнять качественно другой репертуар (песни итальянского движения сопротивления, песни из пьес Бертольта Брехта) и т. д. В последующие годы она исполняла главную роль в «Трёхгрошовой опере» Джорджо Стрелера, которая демонстрировалась в нескольких городахЗападной Европы. Альбомы Мильвы были сертифицированы какзолотые и платиновые в Западной Германии. В 2006 году она была награждена Орденом «За заслуги перед Федеративной Республикой Германия» первой степени. Высшие награды государства певица также получила на своей родине в Италии (Орден «За заслуги перед Итальянской Республикой», 2007) и во Франции (Орден почетного легиона, 2009)
За 55-летнюю карьеру (на 2014 год), длящуюся без творческих пауз, Мильва выпустила 65 студийных и 13 «живых» альбомов, выпустила в общей сложности более 1000 песен на итальянском, французском, немецком, английском, испанском, японском, греческом, неаполитанском и корейском языках[1].
Интересные факты[править | править вики-текст]
|
В этом разделе не хватает ссылок на источники информации.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 20 сентября 2011. |
- Творчество Мильвы чрезвычайно широко и многопланово: в репертуаре певицы более 1000 песен на 9 языках (итальянском, немецком, французском, английском, испанском, греческом, японском, корейском и неаполитанском диалекте итальянского), помимо эстрадной песни Мильва поёт оперные партии, диско, рок, считается одной из лучших европейских исполнительниц танго.
- Творчество певицы имеет много пересечений с русской культурой: в репертуаре певицы есть собственные трактовки таких песен, как «Катюша» («Fischia il vento»), «Lungo la strada» (в итальянском прокате второе название у песни — «Poljushko pole»), «Cavalli bradi» (переложение известной песни Владимира Высоцкого«Кони привередливые» в память о певце), «Сизокрылый птах» (популярный в СССР в исполнении Софии Ротару на украинском языке. В репертуаре С. Ротару есть эта же песня, исполненная на языке оригинала — итальянском («L’immensita»). Инструментальная версия песни Мильвы «Little man» даже вошло в музыкальное сопровождение культового мультфильма «Ну, погоди!». Кроме песен, Мильва в своих концертах нередко читает стихи Марины Цветаевой. В 1986 году Мильва приезжала в СССР для участия в программе «Цветы и песни Сан-Ремо в Москве» и вместе с Аллой Пугачёвой и Олегом Шацковым выступила соведущей этого концерта. Также в нем выступила и племянница Мильвы — Лена Биолкати, как победитель фестиваля Сан-Ремо-86;
- Мильва исполняла «Аллилую» в сопровождении симфонического оркестра на присуждении Нобелевской премиив Осло;
- У певицы в Италии несколько сценических «титулов»: Пантера из Горо (по названию местечка, где родилась певица, и по накалу темперамента и харизматичной внешности), Росса (Rossa — в переводе с итальянского «рыжая») — не только по названию цвета волос певицы (ставшего неотъемлемой частью имиджа Мильвы), но и как подчеркивание яркой индивидуальности певицы (в репертуаре Мильвы даже появилась одноименная песня, давшая название одному из альбомов — «La rossa») и наиболее почетное и лаконичное — Grande Milva (Великая Мильва);
- В 1961 году Мильва выступает в парижской «Олимпии» с программой из песен Э.Пиаф. Примечательно то, что при живой Пиаф на такой смелый шаг не решался ни один исполнитель. Мильва и в дальнейшем будет отдавать дань уважения великой певице — в 1993 году Мильва совершает большое турне, исполняя исключительно песни Эдит Пиаф;
- В репертуаре Мильвы классические арии Баха, Генделя, Шумана, произведения Штокхаузена. Певица участвует в театральных постановках в качестве актрисы и певицы: хореографическая драма «Голубой ангел» по романуГенриха Манна, в 2002 году в «Штатсопер» (Гамбург) с участием певицы семь раз прошла «Истинная история»Лучано Берио по либретто Итало Кальвино, «Трехгрошевая опера» по пьесе Бертольда Брехта (наЭдинбургском фестивале Мильву признали «лучшей из живущих ныне исполнительниц Брехта»), опереттаШтрауса «Летучая мышь» (Мильва исполняет мужскую роль графа Орловского) и др. Также Мильва частый гость сборных оперных концертов: в Арена ди Вероне выступает на одной сцене с Хосе Каррерасом и Ренато Брузоном (англ.)русск., в 2008 году в Дрездене состоялся фестиваль под названием «Diva maxima», посвященный трём выдающимся певицам, любимым в Германии, — Мильве, Монсерратт Кабалье и немецкой диве Ангелике Милстер (нем.)русск..
Дискография[править | править вики-текст]
Альбомы[править | править вики-текст]
|
|
Фотореализм — направление в живописи |
Фотореализм
- Это статья о направлении живописи. Также фотореализмом называют направление компьютерной графики, стремящееся к тому, чтобы конечное изображение было неотличимо от фотографии.
Фотореализм — направление в живописи, возникшее в США в конце1960-х, а затем, распространившееся в 1970-х годах в Европе. Термин, тем не менее, преимущественно применяется по отношению к работам американских фотореалистов конца 1960-х — начала 1970-х годов.
Содержание
[убрать]
Стиль и история[править | править вики-текст]
Слово «фотореализм» было придумано Луи Мейзелем (Louis K. Meisel) в 1968 году, а впервые опубликовано — в 1970 году в каталоге Музея Уитни для выставки «Двадцать два реалиста»[1] Луи Мейзель, двумя годами позже составил определение фотореализма из пяти пунктов по просьбе Стюарта М. Спейсера (Stuart M. Speiser), который владел большой коллекцией работ фотореалистов, которая позже демонстрировались на передвижной выставке «Фотореализм 1973: коллекция Стюарта М. Спейсера» («Photo-Realism 1973: The Stuart M. Speiser Collection.») [1]Определение было следующим:
1. Фотореалист использует камеру и фотографию для сбора информации
2. Фотореалист использует механические и электромеханические средства для переноса информации на холст
3. Фотореалист должен иметь техническую возможность сделать финальный результат выглядящим фотографически
4. Художник должен иметь выставленную работу как фотореалист от 1972 года для того, чтобы считаться значительным фотореалистом
5. Художник должен посвятить как минимум пять лет созданию и показу работ в стиле фотореализма[2]
Фотореалистичная живопись невозможна без фотографии. В фотореализме изменение и движение должно быть заморожено во времени, которое скрупулёзно должно было быть представлено художником.[2] Фотореалисты собирали свои образы и информацию при помощи камеры и фотографий. Обычно снимки делались на слайд, а затем переносились на холст. Это делалось при помощи проецирования слайда или с использованием сетки.[3]Результат был копией фотографии, но обычно гораздо больше оригинала.
Художники[править | править вики-текст]
Первое поколение американских фотореалистов включало таких художников как Ричард Эстес (Richard Estes), Ральф Гоингз (Ralph Goings), Чак Клоуз (Chuck Close), Чарлз Белл (Charles Bell), Джон Баедер (John Baeder), Одри Флэк(Audrey Flack), Дон Эдди (Don Eddy), Роберт Бештле (Robert Bechtle), Том Блэквэлл (Tom Blackwell), и Ричард МакЛин (Richard McLean). Дуэйн Хансон (Duane Hanson) и Джон ДеАндреа (John DeAndrea) были скульпторами, чье творчество связывают с фотореализмом, благодаря раскрашенной очень натуралистичной скульптуре, изображающей обычных людей.
Фотореализм на рубеже тысячелетий[править | править вики-текст]
Подъем фотореализма был в середине 1970-х, но в начале 1990-х интерес к жанру возродился. Этот возобновленный интерес связан как с художниками «первого поколения» фотореалистов, так и с более молодыми. С новыми технологиями возможности художников расширились. Многие известные молодые фотореалисты европейцы: Рафаэлла Спенс (Raphaella Spence) — англичанка, живущая в Италии, Бертран Мениель (Bertrand Meniel) во Франции, Роберто Бернарди (Roberto Bernardi) и Чиара Албертони (Chiara Albertoni) в Италии, Бернардо Торренс (Bernardo Torrens) в Испании, Тони Брунелли (Tony Brunelli) в Нью-Йорке и Клайв Хэд (Clive Head) в Великобритании. Среди азиатских фотореалистов известен иранец Иман Малеки.
Источники[править | править вики-текст]
- Photorealism by Louis K. Meisel. Abradale/Abrams, New York, NY, (1989).
- Photorealism Since 1980 by Louis K. Meisel. Harry N. Abrams, New York, NY, (1993).
- Photorealism at the Millennium by Louis K. Meisel and Linda Chase. Harry N. Abrams, New York, NY, (2002).
- Charles Bell: The Complete Works, 1970—1990 by Henry Geldzahler, Louis K. Meisel,Abrams New York, NY(1991).
- Richard Estes: The Complete Paintings, 1966—1985 by Louis K. Meisel, John Perreault, Abrams New York, NY (1986).
- Richard Estes by John Wilmerding. Rizzoli, New York, NY, (2006).
- Robert Bechtle: A Retrospective by Michael Auping, Janet Bishop, Charles Ray, and Jonathan Weinberg. University of California Press, Berkeley, CA, (2005).
- Ralph Goings: Essay/Interview by Linda Chase. Harry N. Abrams, New York, NY, (1988).
|
Художник - иллюстратор Бруно Вагнер (Bruno Wagner) |
Художник - иллюстратор Бруно Вагнер (Bruno Wagner) так же известен почитателям его таланта под ником Yayashin. Этот талантливый художник-иллюстратор появился на свет в 1979.Его родина город Страсбург в северо-восточной Франции. Рассматривая его картины на фэнтези темы, трудно поверить, что они созданы при помощи цифровой графики. Авторские работы художника Бруно Вагнера (Bruno Wagner) больше похожи на живопись, выполненную классическими методами при помощи кисти .Такой удивительный эффект достигнут при помощи многолетнего упорного труда Бруно Вагнера( Bruno Wagner).Некоторые свои картины художник сначала рисует масляными или акриловыми красками на холсте, а потом переносит изображение на экран монитора, а некоторые работы полностью создает ,с помощью различных компьютерных программ ,только в цифровой графике. Основными действующими лицами его произведений являются демонессы , прекрасные женщины из призрачного мира, мифические существа, различные химеры и прочие фантастические образы. Художник-иллюстратор Бруно Вагнер (Bruno Wagner) так же известен в качестве иллюстратора литературных произведений на фэнтези и фантастические темы. Многие из книжных обложек на книжных полках могут похвастаться тем ,что их иллюстрировал талантливый художник –иллюстратор Бруно Вагнер (Bruno Wagner).
http://vision7.ru/publ/miry_fentezi/khudozhnik_ill...vagner_bruno_wagner/8-1-0-3704
























|
Процитировано 1 раз
Понравилось: 2 пользователям
Изомальтит (палатинит) — O-α-D-глюкопиранозил-D-маннит |
Изомальтит
| Изомальтит | |
 |
|
| Общие | |
|---|---|
|
Систематическое наименование |
Изомальт
|
| Хим. формула | C12H24O11 |
| Физические свойства | |
| Молярная масса | 344,31236 г/моль |
| Классификация | |
| Рег. номер CAS | 64519-82-0 |
| PubChem | 88735 |
| SMILES | |
| ChemSpider | 80068 |
| Приводятся данные для стандартных условий (25 °C, 100 кПа), если не указано иного. | |
Изомальтит (палатинит) — O-α-D-глюкопиранозил-D-маннит, бесцветные, сладкие на вкус кристаллы, растворимые в воде.
Изомальтит синтезируют из сахарозы, изомеризуя её на первой стадии в изомальтулозу с её последующим каталитическим гидрированием над никелем Ренея. Гидрирование ведет к восстановлению карбонильной группы фруктозного остатка изомальтулозы, при этом образуются два изомерных глюкопиранозилальдита — мальтит и изомальтит.
По сладости изомальтит близок к сахарозе (0,5 сладости сахарозы), но плохо всасывается в кишечном тракте, используется как подсластитель исахарозаменитель при производстве продуктов для диабетиков. Изомальт встречается в природе в сахарном тростнике, сахарной свёкле и мёде. В пищевой промышленности известен и зарегистрирован в качестве пищевой добавки Е953.
Содержание
[убрать]
Свойства изомальта[править | править вики-текст]
Среди наиболее важных свойств изомальта можно назвать следующие[1]:
- 1 грамм изомальта содержит 2,4 ккал = 10 кДж. Это говорит о том, что изомальт относительно низкокалорийный продукт.
- Обладает низким гликемическим индексом (рекомендуется для больных сахарным диабетом)
- Является пробиотическим (Пробиотическими — «поддерживающими жизнь» являются продовольственные продукты, содержащие живые микроорганизмы, которые улучшают равновесие между поддерживающими здоровье и вредными для него микроорганизмами в кишечном тракте. Они оказывают позитивное воздействие на весь организм человека. Пробиотические продукты создают самые благоприятные условия для развития микрофлоры, улучшающей здоровье.). Создаёт чувство сытости.
- Позволяет избежать резких колебаний сахара в крови и адаптировать подачу энергии в организм.
- Повышая саливацию, он снижает кислотность и увеличивает содержание кальция в поверхностной части зуба, что способствует восстановлению зубной эмали. Если пищевой продукт не снижает рН ротовой полости ниже 5,7 в течение 30 мин. после его приёма, то он может, согласно положению FDA, применяться с обозначением «не вызывает кариеса». Такое обозначение имеют продукты, содержащие изомальт.
- Вызывает прилив сил, действует длительное время, обеспечивая равномерную энергоподпитку.
- Стимулирует активную работу кишечника.
- Обладает слабительными свойствами.[2]
- В многочисленных исследованиях доказано, что приём изомальта незначительно влияет на уровень глюкозы иинсулина у здоровых людей и больных диабетом 1-го и 2-го типа (G. Siebert и соавт., 1975; W. Bachmann и соавт., 1984; D. Thiebaud и соавт., 1984; М. Drost и соавт., 1980).
Этот сахарозаменитель был впервые получен в 1956 г. в Stodola как побочный продукт в процессе производства декстранов из сахарозы.
После того как в 1990 году изомальт был признан безопасным продуктом и получил разрешение на использование в США, его стали использовать при приготовлении различных продуктов по всему миру.
Объединённый комитет экспертов по пищевым добавкам ВОЗ также признал его безвредность и одобрил его ежедневное употребление без ограничений.[источник не указан 1655 дней] В сутки изомальта в чистом виде рекомендуют употреблять не более 30 грамм (по данным сайта diabet.ru).
Применение изомальта[править | править вики-текст]
Изомальт придаёт продуктам объём, обеспечивает требуемую структуру, среднюю сладость. Поэтому его часто используют при приготовлении кондитерских изделий:
- шоколада,
- грильяжа,
- мягкой и твёрдой карамели,
- драже,
- мороженого,
- конфитюров,
- жевательной резинки,
- других пищевых продуктов.
Применение изомальта в кондитерской отрасли даёт существенные технологические преимущества. Данные изделия не размягчаются и не липнут к рукам, что позволяет упаковывать их в общую коробку без дополнительной обёртки. Поскольку изомальт не вызывает кариеса зубов, в отличие от других подсластителей, и его температура плавления около 145 °C, его можно использовать при термообработке и в экструзионных процессах, в том числе в фармацевтической промышленности.
Заменитель сахара, который производится обычно из свекловичного сахара, имеет такой же вкус как сахар. Получают из 100 % растительного сырья, без добавления искусственных сахарозаменителей, консервантов, ароматизаторов, красителей и улучшителей вкуса. Является безвредным для зубов, так как не является источником питания для бактерий, которые вырабатывают вредную кислоту во рту.
- Безопасные дозы до 50 г/день для взрослых и 25 г/день для детей.
- Низкокалорийный и диетический продукт (1 г изомальта содержит всего 2,4 ккал = 10 кДж). Гликемический индекс — 2.
- Внешне выглядит, как мелкоперемолотый сахар.
- Не вызывает быстрого увеличения содержания глюкозы в крови (как при приеме сахара), что позволяет применять его в продуктах для диабетиков.
- Организм усваивает изомальт в значительно меньших количествах и более медленно по сравнению с сахаром. Соответственно, уровень сахара и инсулина не изменяются так быстро, как это происходит при приеме сахара.
- Относится к классу пребиотиков, обладает свойствами растительной клетчатки и работает как балластное вещество, создавая чувство сытости и заполнения желудка.
- Действует на пищеварительную систему подобно диетической клетчатке, стимулируя активную работу кишечника, но при избыточном количестве стимулируя также диарею и метеоризм
- Получил одобрение Объединённого комитета по пищевым добавкам (JECFA), Всемирной организации здравоохранения (WHO) и Научного комитета по пищевым продуктам Европейского Сообщества (EEC Scientific Committee of Food).
См. также[править | править вики-текст]
|
30 цитат Бернарда Шоу против нытья и лени |
|
Процитировано 1 раз
Понравилось: 2 пользователям
инстограмм |
 |
|
| Тип |
фото- и видео-приложение |
|---|---|
| Автор |
Дан и Арм |
| Разработчик |
Instagram, Inc. |
| Написана на |
Python |
| Операционная система |
iOS 6.0 или новее, |
| Языки интерфейса |
Русский, Английский, Голландский, Испанский, Итальянский, Корейский, Немецкий, Упрощенный китайский, Французский, Африкаанс (Бурский), Греческий, Датский, Индонезийский, Малайский, Норвежский (букмол), Польский, Португальский, Тагальский, Тайский, Традиционный Китайский, Турецкий, Финский, Чешский, Шведский, Японский |
| Первый выпуск |
6 октября 2010 года |
| Последняя версия |
Android: 6.12.1[1] (18 декабря 2014 года) |
| Лицензия | |
| Сайт | |
| Instagram на Викискладе | |
Instagram — бесплатное приложение обмена фотографиями ивидеозаписями, позволяющее снимать фотографии и видео, применять к ним фильтры, а также распространять их через свой сервис и ряд другихсоциальных сетей[4]. Instagram делает фотографии квадратной формы — как камеры моментальной фотографии Polaroid, Kodak Instamatic исреднеформатные камеры 6×6 (большинство же мобильных фотоприложений использует соотношение сторон 3:2).
Приложение совместимо с устройствами iPhone, iPad и iPod Touch на iOS4.3 и выше, а также с телефонами на Android 2.2 и выше с поддержкойOpenGL ES 2. Распространяется оно через App Store и Google Playсоответственно[5]. 21 ноября 2013 года появился Instagram Beta дляWindows Phone[6].
В апреле 2012 года Instagram был приобретён компанией Facebook. Цена покупки составила 300 млн долларов денежными средствами и 23 млн акций компании, что в общей сложности составило $1 млрд[7].
Содержание
[убрать]
История[править | править вики-текст]
Разработка Instagram началась в Сан-Франциско, когда Кевин Систром и Майк Кригер решили переориентировать свой проект Burbn на мобильные фотографии[8][9]. Приложение появилось в магазине приложений App Store компании Apple 6 октября 2010 года[10].
Вскоре после выпуска приложения к команде присоединился Джош Ридель в качестве менеджера сообщества. В ноябре 2010 года к команде присоединился Шейн Суини в качестве инженера, а в августе 2011 года — Джессика Золлман как ИТ-евангелист сообщества[11][12][13].
В январе 2011 года в приложение были добавлены хэштеги для того, чтобы было легче находить пользователей и фотографии[14].
В сентябре 2011 года была выпущена версия приложения 2.0, в которой появились живые фильтры, мгновенное изменение наклона, четыре новых фильтра, фотографии высокого разрешения, опциональные границы, поворот одним кликом и обновлённая иконка[15].
В апреле 2012 года была выпущена версия приложения для платформыAndroid[16], которое за сутки было скачано более миллиона раз[17].
9 апреля 2012 года Facebook объявил о покупке мобильного фотоприложения Instagram за $1 млрд. Владельцам фотосервиса Facebook перечислит 300 миллионов долларов и передаст около 23 миллионов своих акций. Кроме того, социальная сеть обязалась в случае срыва сделки выплатить Instagram неустойку в 200 миллионов долларов[18]. В связи с покупкой 25 июня вышло обновление 2.5.0, в результате которого в Instagram появилась более тесная интеграция с Facebook.
В августе 2012 года каждую секунду в Instagram ставилось 575 лайков и добавлялся 81 комментарий. На Instagram пользователи проводили в среднем 257 минут в месяц, что на полтора часа больше, чем на Твиттер.[19]
В конце 2012 года Instagram анонсировал изменение правил пользовательского соглашения. Среди нововведений должен был появиться пункт, что Instagram получает права на использование фотографий, загруженных его пользователями, в том числе в рекламных целях.[20] Это вызвало резкую критику в обществе, как среди участников Instagram, так и со стороны юристов по авторскому праву. Многие участники Instagram удалили свои учётные записи. По данным аналитической службы AppData, Instagram, возможно, потерял до 25 % пользователей — его ежедневная посещаемость снизилась с 16 млн до 12 млн человек.[21] Столкнувшись с критикой и протестами, руководство сервиса переформулировало спорный пункт пользовательского соглашения, заявив, что их намерения были неправильно поняты[22].
В апреле 2013 года Instagram сообщил о начале внедрения своей новой разработки, которая позволит пользователям отмечать на фотоснимках себя, своих друзей, интересные места, а также известные бренды. Также будет предоставлена возможность настраивать систему уведомлений о новых отметках и в том числе делать их приватными[23].
В июне 2013 года Instagram анонсировал возможность записи видео длиной в 15 секунд.
8 августа 2013 года появилась интеграция с социальной сетью «ВКонтакте»[24].
21 ноября 2013 года была выпущена версия Instagram для Windows Phone 8.
Масштабы[править | править вики-текст]
К декабрю 2010 года у Instagram был один миллион зарегистрированных пользователей[25]. В июне 2011 года — уже пять миллионов[26]. К сентябрю это число удвоилось[27], а к марту 2012 года количество пользователей достигло почти 30 миллионов[28]. К концу февраля 2013 года Instagram объявил о 100 миллионах активных пользователей[29]. А в конце марта 2014 года Марк Цукерберг заявил о регистрации 200-миллионного пользователя[30].
В июле 2011 года Instagram объявил о 100 миллионах загруженных фотографий. В августе того же года их число достигло 150 миллионов[31][32]. К ноябрю 2013 пользователи загрузили уже 16 миллиардов снимков[33].
Финансирование[править | править вики-текст]
5 марта 2010 года, во время работы над приложением Burbn, Систром закрыл раунд финансирования в размере 500 000 долларов от Baseline Ventures и Andreessen Horowitz[34].
2 февраля 2011 года было объявлено, что Instagram привлёк 7 миллионов долларов от различных инвесторов, в том числе от Benchmark Capital, Джека Дорси, Криса Сакка (через фонд LOWERCASE Capital) и Адама Д’Анджело[35].
Награды[править | править вики-текст]
- В январе 2011 года Instagram занял второе место в номинации «Лучшее мобильное приложение» в конкурсе 2010 TechCrunch Crunchies[36].
- В мае 2011 года журнал Fast Company поставил CEO Кевина Систрома на 66-е место в списке «100 самых креативных людей в бизнесе в 2011 году»[37].
- В июне 2011 года журнал Inc включил сооснователей Систрома и Кригера в список «30 тех, кому нет 30»[38].
- В сентябре 2011 года Instagram выиграл в номинации «Лучшее местное приложение» в конкурсе SF Weekly Web Awards[39].
- В 2011 году Систром и Кригер появились на обложке сентябрьского выпуска журнала 7x7[40].
- В декабре 2011 года Apple выбрала Instagram «приложением года для iPhone»[41].
Instagram устройства и сервисы[править | править вики-текст]
Популярность приложения спровоцировала появление множества разработок, так или иначе связанных с Instagram. В качестве отдельного направления таких разработок можно выделить проекты разнообразных устройств, предназначенных для работы с Instagram.
Первым из таких устройств является Instagram Socialmatic Camera — камера, дизайн которой выполнен в стиле иконки Instagram. Камера позволяет сразу обработать фотографию и отправить её в Instagram, а также моментально распечатать фотографию. Таким образом, разработчики устройства хотят перенести Instagram в реальный мир, предлагая пользователям делиться фотографиями не только в социальной сети, но и в жизни[42]. Первые модели продукта ADR студии и Polaroid, которые можно будет купить уже в этом году, будут иметь два объектива, сенсорный дисплей, мини-принтер с 4-мя картриджами, оптический зум, 3G модуль, а также оснащеныWiFi и Bluetooth.[43]
Вторым устройством является специальная цифровая фоторамка Instacube, которая также выполнена в стилистике иконки Instagram и умеет показывать на своем экране фотографии из ленты выбранного Instagram аккаунта.
Также появляются сервисы, позволяющие напечатать фотографии пользователей Instagram на различных предметах — магниты, подушки, футболки, холсты и др.
|
Теллурические токи (также земные токи) |
Земные токи
Теллурические токи (также земные токи) — электрические токи, которые текут у поверхности земной коры[1]. Впервые обнаружены в проволоке, соединяющей две более или менее удаленные друга от друга точки земной поверхности. В условиях современных лабораторий земные токи обнаруживает потенциометр путём наблюдения разности потенциалов между двумя электродами, помещенными в разные точки земного грунта. В современной науке земные токи объясняются вращением Земли, при котором происходит трение между земной поверхностью и слоями атмосферы. Происхождение земных токов приписывали также движению Земли в электрическом или магнитном поле
Обнаружение[править | править вики-текст]
Фокс и Беккерель (1830), исходя из теории магнетизма Ампера, искали и нашли подобные токи в земной поверхности. Позже, когда телеграфы покрыли поверхность земли сетью проводов с концами, погруженными в землю, земные токи, нередко вызывавшие в этих проводах сильные электрические возмущения, начали подвергаться более тщательному изучению. Исследование земных токов производилось Барловым (1849) и Эри (1860—90) в Англии, Гейсигом в Германии, Пальмиери в Италии, Блавье (1884) и Маскаром (1890, в обсерватории Сен-Мор около Парижа), П. Бахметьевым в Болгарии (1892—1893) и после 1882 г. производились в г. Павловске Г. Вильдом.
Значение и гипотезы[править | править вики-текст]
Для наблюдения земных токов соединяют концы изолированной проволоки с двумя металлическими пластинами, закопанными в землю на расстоянии 1 км или более друг от друга. В проволоку вводится гальванометр, показания которого наблюдают через известные промежутки времени. Познания о земных токах долгое время оставались весьма скудными. Более или менее несомненны лишь следующие факты:
- напряжение тока между точками, удаленными на 1 км, колеблется обыкновенно от 0 до 0,06 вольта;
- направление токов непрерывно меняется, наиболее часто от SW к NE;
- суточный ход токов представляет довольно ясно выраженный Мах. и Min., проявляющиеся в разных местах в разное время;
- токи находятся в несомненной, но неясной связи с изменениями магнитного состояния Земли и с явлением атмосферного электричества;
- сильные токи вообще не совпадают по времени с сильными магнитными и электрическими возмущениями.
Большинство ученых приводит явления токов в связь с магнитными свойствами Земли. Из них одни видят в токах причину, другие следствие магнитности Земли. Некоторые (Прис, Вильд) указывают на связь токов с явлением солнечных пятен, другие (Бахметьев) видят в них термоэлектрические явления и приводят их в связь с ходом суточной температуры, третьи (Ландезеер) приписывают их электризации ветром поверхности Земли и т. д.
Литература[править | править вики-текст]
- Дари, «Электричество в природе» (пер. Д. Голова),
- П. Бахметьев «Происхождение земных токов» (журнал «Электричество», 1894, стр. 88 и 118).
См. также[править | править вики-текст]
|
Малкольм Икс афроамериканский исламский духовный лидер и борец за права человека. |
Малкольм Икс
| Малкольм Икс | |
| Malcolm X | |
 Малкольм Икс в марте 1964 года |
|
| Имя при рождении: |
Малкольм Литтл |
|---|---|
| Дата рождения: | |
| Место рождения: | |
| Дата смерти: |
21 февраля 1965 (39 лет) |
| Место смерти: | |
| Гражданство: | |
| Вероисповедание: |
ислам суннитского толка |
| Основные идеи: | |
| Род деятельности: | |
| Супруга: |
Бетти Шабазз |
| Дети: |
Атталла, Кубила, Ильяса, Гамила Лумумба, Малика, Маллак |
| Автограф | |
| Малкольм Икс на Викискладе | |
Малкольм Икс (англ. Malcolm X), или эль-Хадж Малик эш-Шабазз[прим. 1] (араб. الحاجّ مالك الشباز; урождённый Малкольм Литтл(англ. Malcolm Little); 19 мая 1925, Омаха, Небраска, США — 21 февраля1965, Нью-Йорк, США) — афроамериканский исламский духовный лидер и борец за права человека. Среди сторонников Икс известен как защитник прав чернокожего населения США, резкий критик американцев европейского происхождения, виновных, по его мнению, в преступлениях против афроамериканцев. Противники Икса обвиняли его в апологии расизма и насилия. Икс был назван одним из наиболее влиятельных афроамериканцев в истории.
В шесть лет Икс лишился отца, который, по слухам, был убит белыми расистами. Семь лет спустя мать Малкольма была помещена в психиатрическую больницу, после чего мальчик оказался в приёмной семье. В двадцать лет он был осуждён за кражу, взлом и проникновение. Находясь в тюрьме, он присоединился к религиозной и националистической афроамериканской организации «Нация ислама», и после освобождения в 1952 году Икс быстро стал одним из её лидеров. На протяжении двенадцати лет он являлся лицом этой группы, отношение к которой было довольно противоречивым. В соответствии с доктриной организации Икс распространял точку зрения опревосходстве чёрных, призывал к разделению американцев европейского и африканского происхождения и насмехался над интеграционными чаяниями активистов движения за гражданские права чернокожих.
В марте 1964 года Икс разочаровался в деятельности «Нации ислама» и её главы Элайджи Мухаммада и в результате отрёкся от организации и её учений. Вскоре он обратился к исламу суннитского толка и отправился в путешествие по Африке и Ближнему Востоку. Вернувшись в Штаты, Икс приступил к формированию Организации афроамериканского единства и «Корпорации „Исламская мечеть“». По-прежнему разделяя панафриканские взгляды и поддерживая права чёрных на самоопределение и самооборону, Икс отказался от своих расистских взглядов, сказав: «Я многое натворил, будучи [чёрным] мусульманином, и теперь я сожалею. Тогда я был зомби… мне указали некоторое направление и приказали маршировать»[1][прим. 2]. В феврале 1965 года Икс был убит одним из членов «Нации ислама».
Содержание
[убрать]
|
Богиня " Артемида " |
Артемида
| Артемида | |
|---|---|
 Артемида Богиня охоты, покровительница всего живого |
|
| Мифология: | Древнегреческая |
| В иных культурах: | Анаит, Диана, Артио |
| Отец: | Зевс |
| Мать: | титанида Лето |
| Дети: | бездетна |
| Иллюстрации на Викискладе? | |
Артеми́да (др.-греч. Ἄρτεμις) — в древнегреческой мифологиидевственная, всегда юная богиня охоты, богиня плодородия, богиня женского целомудрия, покровительница всего живого на Земле, дающая счастье в браке и помощь при родах[1], позднее богиня Луны(её брат Аполлон был олицетворением Солнца). У Гомера — образ девичьей стройности, покровительница охоты[2]. У римлян отождествлялась с Дианой.
Культовыми животными Артемиды стали лань и медведица.
Содержание
[убрать]
Мифология и культ[править | править вики-текст]
Этимология имени Артемида (др.-греч. Ἄρτεμις) неясна, возможные варианты: «медвежья богиня», «владычица», «убийца»[3]. Микенск. a-ti-mi-te[4].
Дочь Зевса и богини Лето, сестра-близнец Аполлона (Hes. Theog. 918)[5], внучка титанов Кея и Фебы. Родилась на острове Делос.
Её прислужницами были 60 океанид и 20 амнисийских нимф[6]. Получила в подарок от Пана 12 псов[7]. Согласно Каллимаху, охотясь на зайцев, радуется виду их крови[8].
Классическая Артемида — вечная дева; сопровождающие её нимфы также дают обет безбрачия, те же, кто не соблюдает его — строго караются (как, например, Каллисто). Перед свадьбой богине приносились искупительные жертвы. Во многих мифах она представляется мстительной и жестокой: убивает Актеона, детей Ниобы, приказываетАгамемнону принести ей в жертву его дочь Ифигению. Губительные функции Артемиды связаны с её архаическим прошлым — владычицы зверей на Крите. В древнейшей своей ипостаси не только охотница, но и медведица[3].
Такая Артемида, которой приносятся человеческие жертвы, во многом близка древним богиням-матерям, подобнымКибеле и Иштар; отсюда, возможно, и оргиастические элементы культа, прославляющего плодородие богини. С ней нередко отождествлялись Илифия, пособница рожениц, Геката — богиня мрака и покровительница чародеев,Селена — олицетворение Луны; Артемида (в своей древней ипостаси), как и многие подобные ей богини, защищает женщин и детей, облегчает страдания умирающих, она ассоциируется одновременно и с рождением, и со смертью.
Любопытны и не совсем понятны связи Артемиды с медведями. В Брауроне, у восточного побережья Аттики, находился раскопанный сейчас храм Артемиды Брауронии. С одной стороны, в этот храм посвящались одежды умерших при родах женщин: это связано с функцией Артемиды как родовспомогательницы и не заключает в себе каких-либо неожиданностей. Но с этим же храмом был связан странный обычай: афинские девочки в возрасте от пяти до десяти лет поселялись на некоторое время в этом храме, назывались ἄρκτοι, «медведицами», и во время справлявшегося раз в четыре года праздника Брауроний осуществляли, одетые в выкрашенные шафраном одежды, какие-то церемонии в честь Артемиды. С этим обычаем сопоставляют аркадский миф о спутнице АртемидыКаллисто, превращенной ею в медведицу, и видят здесь следы древнего териоморфного, то есть «звериного» облика самой Артемиды[9].
Согласно Котте, Артемид было три[10]: дочь Зевса и Персефоны, родила крылатого Эрота от Гермеса; дочь Зевса третьего и Лето; дочь Уписа и Главки, которую называют Упис.
По египетскому преданию, которое сообщил эллинам Эсхил, Артемида — дочь Деметры[11]. Когда боги бежали в Египет, она превратилась в кошку[12].
Культ Артемиды был распространён повсеместно, но особенно славился её храм в Эфесе в Малой Азии, где почиталось изображение Артемиды «многогрудой». Эфесский храм, где находилась прославленная многогрудая статуя богини-покровительницы деторождения. Первый храм Артемиды сжёг в 356 до н. э., желая «прославиться»,Герострат. Построенный на его месте второй храм был одним из семи чудес света. Артемида Эфесская являлась покровительницей амазонок.
Эпитеты[править | править вики-текст]
- Агротера. «Охотница», «Ловчая». Эпитет Артемиды, её храм в Аттике[13]. Либо некая богиня[14].
- Алфеея.
- Апанхомена. («Удавленница»). Эпитет Артемиды в Кафии (Аркадия), с которым связана легенда[15]. Согласно Каллимаху, аркадцы молятся Артемиде Удавившейся[16].
- Арикийская.
- Ариста. Эпитет Артемиды, о эпитете есть другой рассказ, который Павсаний обходит молчанием[17].
- Астратея.
- Браврония. Эпитет Артемиды, от аттического дема Браврон[18]. Праздники связаны с переодеванием в медведиц[19].
- Бромия. Эпитет Артемиды[20].
- Гегемона. «Водительница». Эпитет Артемиды[21]. В Тегее с ним связана легенда[22].
- Геката. Так называют Артемиду[23].
- Гекаэрга. Также это эпитет Артемиды[24].
- Гиакинфотрофос. Эпитет Артемиды в Книде[25].
- Дафния. Эпитет Артемиды[26].
- Делия. Эпитет Артемиды[27]. Имя возлюбленной Тибулла.
- Евклея.
- Евринома. По фигалейцам, эпитет Артемиды[28].
- Каллиста. Эпитет Артемиды[17]. Первым его использовал поэт Памф, заимствовав у аркадян. Храм Артемиды Каллисты стоял рядом с могилой Каллисто[29].
- Кариатида. Эпитет Артемиды. Кариаты — жрецы Артемиды[30]. Кастор и Полидевк обучили спартанцев в местечке Карии особому виду пляски[31]. en:Caryatis
- Кинфия. Эпитет Артемиды. От горы Кинф на Делосе[32]. Имя возлюбленной Проперция.
- Колоенская. Эпитет Артемиды. Святилище у озера Колоя в Лидии[33].
- Кордака. Эпитет Артемиды в Элиде[34].
- Лафрия (Λαφρία). Эпитет Артемиды у калидонян и мессенцев по имени героя Лафрия, установившего культ Артемиды в Калидоне (см. Мифы Фокиды)[35], также в Патрах[36].
- Левкофрина. «Белобровая». Эпитет Артемиды, почитаемой магнетами[37].
- Лигодесма. «Обвязанная ивами». Эпитет Артемиды Орфии в Спарте[38].
- Лохия. «Родовспомогательница». Эпитет Артемиды[39].
- Мелисса (Μέλισσα, «пчела»). В Эфесе эпитет Артемиды, названной дочерью Деметры. Учреждение культа описано в трагедии Эсхила «Жрицы» (фр.86-87 Радт). Мелиссами называли жриц Деметры[40].
- Мунихия. Эпитет Артемиды[41]. Её святилище в городке Пигелы в Ионии, основанном Агамемноном[42]. КсоанАртемиды Мунихии в Сикионе соорудили Скиллид и Дипен[43].
- Орфия. (Ортия.) Эпитет Артемиды[44], её алтарь в Спарте.
- Орфосия. (Ортосия.) Эпитет Артемиды[45]. Так называют амазонку Антиопу[46].
- Пайдотрофа. «Детокормилица». Эпитет Артемиды. Храм в Короне (Мессения)[47].
- Подагра. По Сосибию, в Лаконике есть жертвенник Артемиды Подагры[16].
- Селасфора. («Светоносная»). Эпитет Артемиды[48].
- Тавриона[49]. См. Тавропола.
- Тавропола. Эпитет Артемиды[50]. Изображение Артемиды Таврической в Бравроне[18]. Обряды Артемиды Таврополы были и в Каппадокии[51]. Эпитет Гекаты[52]. Согласно Питоклу, фокейцы устраивают ей человеческие всесожжения[53].
- Улия.
- Феба.[54] Имя Артемиды[55].
- Ферея. Эпитет Артемиды[56]. Связан с Ферами, статуя в Аргосе[57].
- Хесийская. Эпитет Артемиды на Самосе[58].
- Хитона. Эпитет Артемиды[59].
- Эфопия. Эпитет Артемиды, её святилище в Митилене[60]. В «Эфиопиде» (синопсис) упомянуто, что на Лесбосе Ахилл приносит жертвы Аполлону, Артемиде и Лето.
Спутницы[править | править вики-текст]
- Гиала. Спутница Артемиды[61].
- Нефела. Спутница Артемиды[61].
- Опис. Нимфа, спутница Артемиды[62].
- Ортигия. Кормилица Артемиды и Аполлона[63]. Её именем назван парк у храма Артемиды в Эфесе, там стояла её статуя с детьми в руках[42].
- Псека. Спутница Артемиды[64].
- Ранида. Спутница Артемиды[61].
- Фиала. Спутница Артемиды[64].
Другие спутницы Артемиды:
- Амнисиады.
- Антиклея.
- Бритомартида.
- Дафна.
- Еврибия (амазонка).
- Крокала.
- Полифонта.
- Прокрида.
- Сиринга.
- Тайгета.
- Феба (амазонка).
- Филоноя (дочь Тиндарея).
|
Понравилось: 1 пользователю
МЕНЕ ПОНРАВИЛОСЬ , А ВАМ ... |
|
Авилова, Лидия Алексеевна |
Авилова, Лидия Алексеевна
| Лидия Авилова | |
 Лидия Алексеевна Авилова |
|
| Имя при рождении: |
Лидия Алексеевна Страхова |
|---|---|
| Дата рождения: | |
| Место рождения: | |
| Дата смерти: |
27 сентября 1943 (79 лет) |
| Место смерти: | |
Ли́дия Алексе́евна Ави́лова (урождённая Стра́хова;3 [15] июня 1864[1], село Клекотки, Тульская губерния — 27 сентября1943, Москва) — русская писательница и мемуаристка.
Её произведения печатались в «Живописном Обозрении», «Севере», «Новом Слове», «Русском Богатстве», «Вестник Европы», «Ниве» и других журналах, книги выходили в издательстве «Посредник».
Содержание
[убрать]
Биография[править | править вики-текст]
Родилась в небогатом дворянском имении Клекотки Епифанского уездаТульской губернии (ныне Скопинский район Рязанской области.
1882 — окончила гимназию в Москве.
1887 — вступила в брак и перебралась из Москвы в Петербург, где и началась её литературная жизнь. В доме Сергея Николаевича Худекова, мужа сестры, редактора и издателя «Петербургской газеты», познакомилась со многими известными литераторами, в том числе знала А. П. Чехова, Л. Н. Толстого, А. М. Горького, И. А. Бунина и других.
1890 — её рассказы начали выходить в петербургских газетах и журналах.
1896 — опубликован первый сборник Лидии Алексеевны: «Счастливец и другие рассказы».
1898 — «Русское богатство» напечатал первую повесть Авиловой «Наследники».
1906 — с семьёй вернулась в Москву, где продолжила плодотворно трудиться:
- «Власть и другие рассказы» (1906),
- «Сын. Рассказ» (1910),
- «Первое горе и другие рассказы» (1913),
- «Образ человеческий» (1914),
- «Пышная жизнь. Камардин» (1918).
1914 — стала членом «Общества любителей российской словесности».
1918 — принята в члены Всероссийского союза писателей.
1922 — писательница выехала в Чехословакию к больной дочери. Прожив два года в атмосфере русской эмиграции, в 1924 году вернулась в Россию.
1929 — избрана почётным членом «Общества А. П. Чехова и его эпохи».
Похоронена в Москве, на Ваганьковском кладбище. Её могила потеряна, родственниками установлен памятный знак на участке 7А Ваганьковского кладбища[2]
Авилова и А. П. Чехов[править | править вики-текст]
Наибольшую известность имеет последняя литературная работа писательницы — мемуары «А. П. Чехов в моей жизни», где она рассказывает о переписке и личных встречах с А. П. Чеховым, и всё произведение выстроено под девизом: «роман, о котором никогда никто не знал, хотя он длился целых десять лет» (да и первоначальное название говорит само за себя — «Роман моей жизни»). Эти мемуары вызвали известные споры: некоторые сочли записки Авиловой полностью достоверными, другие подошли к ним критически, считая взгляд писательницы слишком субъективным, а некоторые эпизоды крайне сомнительными.
Известно, что Лидия Алексеевна познакомилась с А. П. Чеховым в 1889 году, с 1892 года вела с ним переписку. Антон Павлович рецензировал её рукописи, содействовал в их публикации, давал профессиональные советы, отмечая излишнюю сентиментальность стиля Авиловой.
Сочинения[править | править вики-текст]
- Авилова Л. А. Счастливец и др. рассказы", СПб., 1896
- Авилова Л. А. Рассказы. Воспоминания. — М.: Сов. Россия, 1984. — 335 с.
- Авилова Л. А. Пышная жизнь: Рассказ // Только час: Проза русских писательниц конца XIX-начала XX века / Сост. В. Учёнова. — М., 1988. — С. 493—504.
См. также[править | править вики-текст]
Примечания[править | править вики-текст]
Литература[править | править вики-текст]
- Авилова Л. А. [30.V.(11.VI)1864-23.IX.1943] // Краткая лит. энциклопедия. — М., 1962. — Т.1. — С. 57.
- Авилова Л. А. [урожд. Страхова] // Русские писатели 1800—1917: Биогр. словарь. — М., 1989. — Т.1. — С. 19—20.
- Невинская И. Н. Авилова Лидия Алексеевна // Русские детские писатели ХХ века: Биобиблиографический словарь. — М.: Флинта; Наука, 1997. — С. 7—8. — ISBN 5-02-011304-2.
- Авилова // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
|
Lidija Percan (Лидия Перцан) |

Lidija Percan - часто называют золотым голосом Истрии, королевой песни Истрии, Истрийской птичкой ...
Lidija Percan родилась под знаком Рыб в Хорватии, в небольшом городке Rakalj, что расположен на юге полуострова Истрия. Выросла в традиционной атмосфере Истрии и в детстве пела в местной приходской церкви. Карьера в шоу-бизнесе началась, когда она переехала в Пуле, где выступая на местных летних террасах, быстро стала любимицей слушателей. Осознавая, что музыкальное мастерство необходимо совершенствовать, совместно со своей подругой Radojka Šverko (хорватское меццо-сопрано) начала брать уроки вокального мастерства у оперной певицы Marije Bunčuga, которая видела в обеих ученицах потенциальных оперных певиц.
Наиболее важной югославской звукозаписывающей компанией в то время была Jugoton, которая дала ей шанс сделать запись, и вот тогда Lidija Percan стала признанной на национальном уровне.
За время своей творческой карьеры Lidija Percan прочно сотрудничала со многими известными композиторами и авторами песен, такими как Nello Milotti, Stipica Kalogjera, Đorđe Novković, Boško Obradović, Đelo Jusić и т.д.
Певица отметила свое 45-летие на Хорватской музыкальной сцене.
Известный поэт Истрии писал: Lidija Percan - это голос, который заставил нас любить петь.
С ЭТО ГО САЙТА http://www.leonidzl.com/forum/viewtopic.php?f=8&t=4356&p=13292#p13292
|
35 лучших вдохновляющих книг |
35 лучших вдохновляющих книг:
1. Ричард Бах - Чайка по имени Джонатан Ливингстон
2. Антуан де Сент-Экзюпери - Маленький принц
3. Януш Леон Вишневский - Одиночество в сети
4. Бодо Шефер - Законы Победителей
5. Пауло Коэльо - Алхимик
6. Ронда Берн - Тайна
7. Михаил Булгаков - Мастер и Маргарита
8. Эрих Мария Ремарк - Три товарища
9. Джон Грэй - Мужчины с Марса, Женщины с Венеры
10. Дуглас Адамс - Автостопом по галактике
11. Крайон - Путешествие домой
12. Робин Шарма - Монах, который продал свой «Феррари»
13. Владимир Чеповой, Анна Ясная - Перекресток
14. Малкольм Гладуэлл - Переломный момент
15. Роберт Пирсиг - Дзен и искусство ухода за мотоциклом
16. Дональд Трамп - Никогда не сдавайся
17. Ричард Брэнсон — К черту все, берись и делай!
18. М.Веллер — Приключения майора Звягина
19. Владимир Довгань - Я был нищим, стал богатым
20. Одри Ниффенеггер - Жена путешественника во времени
21. Элизабет Гилберт - Есть. Молиться. Любить.
22. Наоми Вульф - Миф о красоте
23. Анна Гавальда - 35 кило надежды
24. Лобсанг Рампа - Ты вечен
25. Роберт Кийосаки - Квадрант денежного потока
26. Стивен Кови - 7 навыков высокоэффективных людей
27. Тимоти Феррис - 4-х часовая рабочая неделя
28. Питер Мейл - Год в Провансе
29. Леви - Искусство быть собой
30. Герман Гессе - Степной волк
31. Карлос Кастанеда - Колесо времени
32. Джек Лондон - Мартин Иден
33. Ричард Ф. Фейнман - Вы, конечно, шутите, мистер Фейнман!
34. Мария Климова - Разговоры в песочнице, или Истории из жизни мам
35. Мусса Лисси - Все, все, все в твоих руках/
|
ХУДОЖНИК JIMMY LAWLOR |
ХУДОЖНИК JIMMY LAWLOR
ВСЁ ЗДЕСЬ http://vdohnovenie2.ru/polet-v-beskrajnosti-shirot-xudozhnik-jimmy-lawlor/
|
Художник Nenad Mirkovich |
Nenad Mirkovich родился в Белграде в 1951 году. Живописью он стал заниматься еще в детстве.
Работа в качестве художника и иллюстратора журнала в Югославии помогла ему развить его разнообразные стили в живописи.
С 1985 года Nenad Mirkovich живет в Хьюстоне, штат Техас.
Люди всех возрастов и различного образа жизни обязательно найдут в творчестве этого талантливого художника картины и образы созвучные их вкусу и настроению.
ВСЁ С ЭТОГО САЙТА http://www.crown6.org/publ/3-1-0-4153











































|
Процитировано 1 раз
С НАСТУПАЮЩИМ 2015 ГОДОМ !!!! |
УРА !!! ТОВАРИЩИ !!!
1.

2.

3.

4.

5.

|
Процитировано 1 раз
Понравилось: 1 пользователю
художник-живописец Сергей Ефошкин |
Сергей Ефошкин – художник-живописец, член Союза Художников России и Международной ассоциации Изобразительных искусств живет и работает в Москве. Окончил Московский Государственный Художественный институт им. В.И.Сурикова Академии художеств. А уже с 1988 года сам стал преподавателем в Российской Академии живописи, ваяния и зодчества. |
ВЕСЬ МАТЕРИАЛ ОТСЮДА http://www.danilovmaster.ru/reproductions_efoshkin.html
























































































|
Тест Тьюринга — эмпирический тест |
Тест Тьюринга
Тест Тьюринга — эмпирический тест, идея которого была предложена Аланом Тьюрингом в статье «Вычислительные машины и разум», опубликованной в 1950 году в философском журнале «Mind». Тьюринг задался целью определить, может ли машина мыслить.
Стандартная интерпретация этого теста звучит следующим образом: «Человек взаимодействует с одним компьютером и одним человеком. На основании ответов на вопросы он должен определить, с кем он разговаривает: с человеком или компьютерной программой. Задача компьютерной программы — ввести человека в заблуждение, заставив сделать неверный выбор».
Все участники теста не видят друг друга. Если судья не может сказать определенно, кто из собеседников является человеком, то считается, что машина прошла тест. Чтобы протестировать именно интеллект машины, а не её возможность распознавать устную речь, беседа ведется в режиме «только текст», например, с помощью клавиатуры и экрана (компьютера-посредника). Переписка должна производиться через контролируемые промежутки времени, чтобы судья не мог делать заключения, исходя из скорости ответов. Во времена Тьюринга компьютеры реагировали медленнее человека. Сейчас это правило тоже необходимо, потому что они реагируют гораздо быстрее, чем человек.
Содержание
[убрать]
История[править | править вики-текст]
Философские предпосылки[править | править вики-текст]
Хотя исследования в области искусственного интеллекта начались в 1956 году, их философские корни уходят глубоко в прошлое. Вопрос, сможет машина думать или нет, имеет долгую историю. Он тесно связан с различиями между дуалистическим и материалистическим взглядами. С точки зрения дуализма, мысль не является материальной (или, по крайней мере, не имеет материальных свойств), и поэтому разум нельзя объяснить только с помощью физических понятий. С другой стороны, материализм гласит, что разум можно объяснить физически, таким образом, оставляя возможность существования разумов, созданных искусственно.
В 1936 году философ Альфред Айер рассмотрел обычный для философии вопрос касательно других разумов: как узнать, что другие люди имеют тот же сознательный опыт, что и мы? В своей книге «Язык, истина и логика» Айер предложил алгоритм распознавания осознающего человека и не осознающей машины: «Единственным основанием, на котором я могу утверждать, что объект, который кажется разумным, на самом деле не разумное существо, а просто глупая машина, является то, что он не может пройти один из эмпирических тестов, согласно которым определяется наличие или отсутствие сознания». Это высказывание очень похоже на тест Тьюринга, однако точно не известно, была ли известна Тьюрингу популярная философская классика Айера.
Несмотря на то, что прошло больше 50 лет, тест Тьюринга не потерял своей значимости. Но в настоящее время исследователи искусственного интеллекта практически не занимаются решением задачи прохождения теста Тьюринга, считая, что гораздо важнее изучить основополагающие принципы интеллекта, чем продублировать одного из носителей естественного интеллекта. В частности, проблему «искусственного полета» удалось успешно решить лишь после того, как братья Райт и другие исследователи перестали имитировать птиц и приступили к изучению аэродинамики. В научных и технических работах по воздухоплаванию цель этой области знаний не определяется как «создание машин, которые в своем полете настолько напоминают голубей, что даже могут обмануть настоящих птиц».[1]
Алан Тьюринг[править | править вики-текст]
К 1956 году британские учёные уже на протяжении 10 лет исследовали «машинный интеллект». Этот вопрос был обычным предметом для обсуждения среди членов «Ratio Club» — неформальной группы британских кибернетиков и исследователей в области электроники, в которой состоял и Алан Тьюринг, в честь которого был назван тест.
Тьюринг в особенности занимался проблемой машинного интеллекта, по меньшей мере, с 1941 года. Одно из самых первых его упоминаний о «компьютерном интеллекте» было сделано в 1947 году. В докладе «Интеллектуальные машины» Тьюринг исследовал вопрос, может ли машина обнаруживать разумное поведение, и в рамках этого исследования предложил то, что может считаться предтечей его дальнейших исследований: «Нетрудно разработать машину, которая будет неплохо играть в шахматы. Теперь возьмем трех человек — субъектов эксперимента. А, В и С. Пусть А и С неважно играют в шахматы, а В — оператор машины. […] Используются две комнаты, а также некоторый механизм для передачи сообщений о ходах. Участник С играет или с А, или с машиной. Участник С может затрудниться ответить, с кем он играет».
Таким образом, к моменту публикации в 1950 году статьи «Вычислительные машины и разум», Тьюринг уже на протяжении многих лет рассматривал возможность существования искусственного интеллекта. Тем не менее, данная статья стала первой статьёй Тьюринга, в которой рассматривалось исключительно это понятие.
Тьюринг начинает свою статью утверждением: «Я предлагаю рассмотреть вопрос „Могут ли машины думать?“». Он подчёркивает, что традиционный подход к этому вопросу состоит в том, чтобы сначала определить понятия «машина» и «интеллект». Тьюринг, однако, выбрал другой путь; вместо этого он заменил исходный вопрос другим, «который тесно связан с исходным и формулируется относительно недвусмысленно». По существу, он предлагает заменить вопрос «Думают ли машины?» вопросом «Могут ли машины делать то, что можем делать мы (как мыслящие создания)?». Преимуществом нового вопроса, как утверждает Тьюринг, является то, что он проводит «чёткую границу между физическими и интеллектуальными возможностями человека».
Чтобы продемонстрировать этот подход, Тьюринг предлагает тест, придуманный по аналогии с игрой для вечеринок «Imitation game» — имитационная игра. В этой игре мужчина и женщина направляются в разные комнаты, а гости пытаются различить их, задавая им серию письменных вопросов и читая напечатанные на машинке ответы на них. По правилам игры и мужчина, и женщина пытаются убедить гостей, что все наоборот. Тьюринг предлагает переделать игру следующим образом: "Теперь зададим вопрос, что случится, если в этой игре роль А будет исполнять машина? Будет ли задающий вопросы ошибаться так же часто, как если бы он играл с мужчиной и женщиной? Эти вопросы заменяют собой исходный «Может ли машина думать?».
В том же докладе Тьюринг позднее предлагает «эквивалентную» альтернативную формулировку, включающую судью, который беседует только с компьютером и человеком. Наряду с тем, что ни одна из этих формулировок точно не соответствует той версии теста Тьюринга, которая наиболее известна сегодня, в 1952 учёный предложил третью. В этой версии теста, которую Тьюринг обсудил в эфире радио Би-Би-Си, жюри задает вопросы компьютеру, а роль компьютера состоит в том, чтобы заставить значительную часть членов жюри поверить, что он на самом деле человек.
В статье Тьюринга учтены 9 предполагаемых вопросов, которые включают все основные возражения против искусственного интеллекта, поднятые после того, как статья была впервые опубликована.
Элиза и PARRY[править | править вики-текст]
Блей Витби указывает на четыре основные поворотные точки в истории теста Тьюринга — публикация статьи «Вычислительные машины и разум» в 1950, сообщение о создании Джозефом Уайзенбаумом программы Элиза(ELIZA) в 1966, создание Кеннетом Колби программы PARRY, которая была впервые описана в 1972 году, и Коллоквиум Тьюринга в 1990.
Принцип работы Элизы заключается в исследовании введенных пользователем комментариев на наличие ключевых слов. Если найдено ключевое слово, то применяется правило, по которому комментарий пользователя преобразуется и возвращается предложение-результат. Если же ключевое слово не найдено, Элиза либо возвращает пользователю общий ответ, либо повторяет один из предыдущих комментариев. Вдобавок Уайзенбаум запрограммировал Элизу на имитацию поведения психотерапевта, работающего по клиент-центрированной методике. Это позволяет Элизе «притвориться, что она не знает почти ничего о реальном мире». Применяя эти способы, программа Уайзенбаума могла вводить в заблуждение некоторых людей, которые думали, что они разговаривают с реально существующим человеком, а некоторых было «очень трудно убедить, что Элиза […] не человек». На этом основании некоторые утверждают, что Элиза — одна из программ (возможно первая), которые смогли пройти тест Тьюринга. Однако это утверждение очень спорно, так как людей, «задающих вопросы», инструктировали так, чтобы они думали, что с ними будет разговаривать настоящий психотерапевт, и не подозревали о том, что они могут разговаривать с компьютером.
Работа Колби — PARRY — была описана, как «Элиза с мнениями»: программа пыталась моделировать поведение параноидального шизофреника, используя схожий (если не более продвинутый) с Элизой подход, примененный Уайзенбаумом. Для того чтобы проверить программу, PARRY тестировали в начале 70-х, используя модификацию теста Тьюринга. Команда опытных психиатров анализировала группу, составленную из настоящих пациентов и компьютеров под управлением PARRY, используя телетайп. Другой команде из 33 психиатров позже показали стенограммы бесед. Затем обе команды попросили определить, кто из «пациентов» — человек, а кто — компьютерная программа. Психиатры лишь в 48 % случаев смогли вынести верное решение. Эта цифра согласуется с вероятностью случайного выбора. Эти эксперименты не являлись тестами Тьюринга в полном смысле, так как для вынесения решения данный тест требует, чтобы вопросы можно было задавать в интерактивном режиме, вместо чтения стенограммы прошедшей беседы.
Почти все разработанные программы и близко не подошли к прохождению теста. Хотя такие программы, как Элиза(ELIZA), иногда заставляли людей верить, что они говорят с человеком, как, например, в неформальном эксперименте, названном AOLiza, но эти случаи нельзя считать корректным прохождением теста Тьюринга по целому ряду причин:
- Человек в таких беседах не имел никаких оснований считать, что он говорит с программой, в то время как в настоящем тесте Тьюринга человек активно пытается определить, с кем он беседует.
- Документированные случаи обычно относятся к таким чатам, как IRC, где многие беседы отрывочны и бессмысленны.
- Многие пользователи Интернета используют английский как второй или третий язык, так что бессмысленный ответ программы легко может быть списан на языковой барьер.
- Многие просто ничего не знают об Элизе и ей подобных программах, и поэтому не сочтут собеседника программой даже в случае совершенно нечеловеческих ошибок, которые эти программы допускают.
Китайская комната[править | править вики-текст]
В 1980 году в статье «Разум, мозг и программы» Джон Сёрль выдвинул аргумент против теста Тьюринга, известный как мысленный эксперимент «Китайская комната». Сёрль настаивал, что программы (такие как Элиза) смогли пройти тест Тьюринга, просто манипулируя символами, значения которых они не понимали. А без понимания их нельзя считать «разумными» в том же смысле, что и людей. «Таким образом, — заключает Сёрль, — тест Тьюринга не является доказательством того, что машина может думать, а это противоречит изначальному предположению Тьюринга».
Такие аргументы, как предложенный Сёрлем, а также другие, основанные на философии разума, породили намного более бурные дискуссии о природе разума, возможности существования разумных машин и значимости теста Тьюринга, продолжавшиеся в течение 80-х и 90-х годов.
Коллоквиум Тьюринга[править | править вики-текст]
В 1990 году состоялась сороковая годовщина публикации статьи Тьюринга «Вычислительные машины и разум», что возобновило интерес к тесту. В этом году произошли два важных события.
Одно из них — коллоквиум Тьюринга, который проходил в апреле в Университете Сассекса. В его рамках встретились академики и исследователи из разнообразных областей науки, чтобы обсудить тест Тьюринга с позиций его прошлого, настоящего и будущего. Вторым событием стало учреждение ежегодного соревнования на получение премии Лёбнера.
Премия Лёбнера[править | править вики-текст]
Ежегодный конкурс «AI Loebner» на получение премии Лёбнера является платформой для практического проведения тестов Тьюринга. Первый конкурс прошел в ноябре 1991 года. Приз гарантирован Хью Лёбнером (Hugh Loebner). Кембриджский центр исследований поведения, расположенный в Массачусетсе (США), предоставлял призы до 2003 года включительно. По словам Лёбнера, соревнование было организовано с целью продвижения вперед в области исследований, связанных с искусственным интеллектом, отчасти потому, что «никто не предпринял мер, чтобы это осуществить».
Серебряная (текстовая) и золотая (аудио и зрительная) медали никогда ещё не вручались. Тем не менее, ежегодно из всех представленных на конкурс компьютерных систем судьи награждают бронзовой медалью ту, которая, по их мнению, продемонстрирует «наиболее человеческое» поведение в разговоре. Не так давно программа «Искусственное лингвистическое интернет-компьютерное существо» (Artificial Linguistic Internet Computer Entity —A.L.I.C.E.) трижды завоевала бронзовую медаль (в 2000, 2001 и 2004). Способная к обучению программаJabberwacky (англ.) побеждала в 2005 и 2006. Её создатели предложили персонализированную версию: возможность пройти имитационный тест, пытаясь более точно сымитировать человека, с которым машина тесно пообщалась перед тестом.
Конкурс проверяет способность разговаривать; победителями становятся обычно чат-боты или «Искусственные разговорные существа» (Artificial Conversational Entities (ACE)s). Правилами первых конкурсов предусматривалось ограничение. Согласно этому ограничению каждая беседа с программой или скрытым человеком могла быть только на одну тему. Начиная с конкурса 1995 года это правило отменено. Продолжительность разговора между судьей и участником была различной в разные годы. В 2003 году, когда конкурс проходил в Университете Суррея, каждый судья мог разговаривать с каждым участником (машиной или человеком) ровно 5 минут. С 2004 по 2007 это время составляло уже более 20 минут. В 2008 максимальное время разговора составляло 5 минут на пару, потому что организатор Кевин Ворвик (Kevin Warwick) и координатор Хьюма Ша (Huma Shah) полагали, что ACE не имели технических возможностей поддерживать более продолжительную беседу. Как ни странно, победитель 2008 года,Elbot (англ.), не притворялся человеком, но всё-таки сумел обмануть трёх судей. В конкурсе проведенном в 2010 году, было увеличено время до 25 минут при общении между системой и исследователем, по требованию спонсора. Что только подтверждает, программы подросли в имитации человеку и только лишь при длительной беседе появляются минусы, позволяющие вычислять собеседника. А вот конкурс проведенный 15 мая 2012 года, состоялся впервые в мире с прямой трансляцией беседы, что только поднимает интерес к данному конкурсу.
Появление конкурса на получение премии Лёбнера привело к возобновлению дискуссий о целесообразности теста Тьюринга, о значении его прохождения. В статье «Искусственная тупость» газеты The Economist отмечается, что первая программа-победитель конкурса смогла выиграть отчасти потому, что она «имитировала человеческие опечатки». (Тьюринг предложил, чтобы программы добавляли ошибки в вывод, чтобы быть более хорошими «игроками».) Существовало мнение, что попытки пройти тест Тьюринга просто препятствуют более плодотворным исследованиям.
Во время первых конкурсов была выявлена вторая проблема: участие недостаточно компетентных судей, которые поддавались умело организованным манипуляциям, а не тому, что можно считать интеллектом.
Тем не менее, с 2004 года в качестве собеседников в конкурсе принимают участие философы, компьютерные специалисты и журналисты.
Стоит заметить, что полного диалога с машиной пока не существует. А то, что есть, больше напоминает общение в кругу друзей, когда отвечаешь на вопрос одного, а следом задаёт вопрос другой или как бы на твой вопрос отвечает кто-то совершенно посторонний. На этом и можно ловить машинную программу, если проверять её по тесту Тьюринга. Можно отметить, что судейство на конкурсе премии Лёбнера — очень забавное занятие, позволяющее с интересом скоротать время.
Судейство на конкурсе очень строгое. Эксперты заранее готовятся к турниру и подбирают весьма заковыристые вопросы, чтобы понять, с кем же они общаются. Их разговор с программами напоминает допрос следователя. Судьи любят, например, повторять некоторые вопросы через определенное время, так как слабые боты не умеют следить за историей диалога и их можно поймать на однообразных ответах[2].
Коллоквиум по разговорным системам, 2005[править | править вики-текст]
В ноябре 2005 года в Университете Суррея проходила однодневная встреча разработчиков ACE , которую посетили победители практических тестов Тьюринга, проходивших в рамках конкурса на получение премии Лёбнера: Робби Гарнер (Robby Garner), Ричард Уоллес (Richard Wallace), Ролл Карпентер (Rollo Carpenter). В числе приглашенных докладчиков были Дэвид Хэмилл (David Hamill), Хью Лёбнер и Хьюма Ша.
Симпозиум общества AISB по тесту Тьюринга, 2008[править
|
ОТВЕТ НУЖЕН СОХРАНЯТЬ ТАМ |
-
это находится в Рязанской области , Шиловский район, п. Дубровка, примерно 1 км от турбазы "Приокская
|
Хроники Акаши |
Хроники Акаши
|
В этой статье не хватает ссылок на источники информации.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 28 ноября 2011. |
Хроники Ака́ши, также акаши́ческие записи[1] — теософский эзотерический, а также антропософский термин, описывающий мистическое знание, закодированное в нефизической сфере бытия. Мистиками считается, что Хроники содержат в себе весь совокупный и коллективный человеческий опыт и историю возникновения Вселенной. Для определения Хроник Акаши используются образные аналогии с «библиотекой», «вселенским компьютером» или «Разумом Бога». Мистиками считается, что содержащаяся в них информация постоянно обновляется с ходом происходящих в мире событий, однако наряду с данными об истории и фактической реальности там могут быть получены и сведения о возможных будущих событиях, а также вневременные «вечные истины». В связи с этим концепция Хроник Акаши мистиками применяется для объяснения феномена ясновидения, а также предлагается в качестве источника вообще всех человеческих открытий, изобретений и произведений как в научной, так и в художественной области творчества. Мистиками предполагается также, что наиболее общим способом контакта с Хрониками для получения нужной информации является метод астральной проекции.
Впервые концепция Хроник Акаши появляется в теософских движениях XIX века, а в XX веке с развитием движениянью-эйдж становится одним из доминирующих понятий философии этого движения. Также с конца XX века в этом же значении часто употребляется описательный наукообразный термин «единое информационное поле Земли» (или: «…Вселенной») или подобные ему, причём он напрямую или косвенно соотносится с понятием «ноосфера», а в качестве его материального соответствия предлагается магнитное (или электромагнитное) поле Земли и/илиионосфера. Развитие технических средств записи информации на магнитных носителях послужило одним из стимулов для выдвижения таких гипотез.
Содержание
[убрать]
История понятия[править | править вики-текст]
Термин «акаша» был заимствован теософскими движениями из индуизма, где он использовался для обозначения первоосновы или первопричины природы; именно из акаши, согласно древнеиндийской философии, возникли базовые первоэлементы (огонь, воздух, земля, вода и эфир) — все вместе они соответствуют пяти органам чувств человека. В древнегреческой философии сходные проблемы решались в ходе дискуссии об архэ, первоначале и первооснове. Близким к акаше греческим понятием может быть назван эфир как пятая особая стихия, либоапейрон, неопределённая первичная стихия, являющаяся источником четырёх определённых стихий и всех определённых вещей в мире.
Принципиальное отличие индуистского понятия «акаша» (особенно если сближать его с греческим «апейроном») от используемого в теософии употребления этого концепта − это то, что в качестве первоосновы мира акаша является совершенно неопределённой, бесформенной тонкой субстанцией, а в качестве источника любых знаний, — напротив, максимально определённой, несущей все определённые знания, всю «определённость» мира.
Использование термина Акаша в смысле общей «эфирной библиотеки» возникло в XIX веке в теософском движении, как и сама концепция получения знаний из пассивного нематериального надличностного и безличного источника. Хотя идея о том, что какие-то тексты не написаны людьми, а открыты им Богом или какими-либо духами в процессеОткровения, очень стара и лежит в основе очень многих религий, в случае Откровения предполагается, что информация передаётся человеку по воле сверхъестественной силы. В теософии же имеет место такая идея, что знания пребывают в каком-то месте и могут быть оттуда извлечены, «считаны» человеком, обладающим соответствующими способностями.
В некотором смысле концепция космического информационного поля «Хроник Акаши» может быть рассмотрена также как эволюция неоплатонического учения о Мировой Душе.
Вероятно, то обстоятельство, что из человеческих чувств акаша соответствует в индуизме слуху и называется иногда «звуконосным эфиром», то есть в некотором роде является той субстанцией, через которую происходит передача информации посредством слов, и позволило теософам назвать Хроники Акаши универсальной базой знаний, источником и хранилищем каждой появившейся мысли, сказанного слова или совершённого действия.
Согласно теософскому учению, осознанный контакт с Хрониками Акаши имели люди древних рас и древних культур нашей расы, откуда они и почерпнули напрямую все свои высокие культурные достижения.
Многие известные личности, в разной степени принимавшие теософскую доктрину, утверждали что они могут использовать Хроники Акаши, среди них: Чарльз Вебстер Лидбитер[2], Эдгар Кейси[3], Анни Безант, Алиса Бейли,Самюэль Аун Веор, Вильям Лилли, Мэнли Палмер Холл, Лилиан Тримонт, Джордж Хант Вильямсон, Рудольф Штейнер[4], Макс Хайндель и Елена Петровна Блаватская.
Критика[править | править вики-текст]
Поскольку существование Хроник Акаши не может быть подтверждено эмпирически, изучение указанных Хроник не рассматривалось в качестве сколько-нибудь серьёзной научной дисциплины. Данное направление знания является неакадемическим. Кроме того, ни христианские, ни индуистские или ведийские традиции не считают, что их священные тексты основаны на какого-либо рода хрониках Акаши.
Хроники Акаши в современной популярной культуре[править | править вики-текст]
Несмотря на неакадемичность Хроник Акаши с сугубо научной точки зрения, они получили довольно широкую популярность в современной культуре, фантастике и фэнтези. Зачастую в фантастике и псевдонаучной литературе используется более «наукообразный» термин — акашическое поле (англ. Akashic Field).
См. также[править | править вики-текст]
Примечания[править | править вики-текст]
- ↑ Иногда в литературе используется менее корректная форма прилагательного «акашеический».
- ↑ Ледбитер Ч. У. «Ясновидение», глава VII
- ↑ Кевин Тодесчи «Эдгар Кейси и хроники Акаши»
- ↑ Штейнер Р. «Из летописи мира (акаша-хроники)»
|
Сомов Константин Андреевич (1869-1939) |
http://gallerix.ru/album/Somov
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

|
|
Хронос |
Хронос
| Хронос (Χρόνος) | |
|---|---|
 Статуя спящего Хроноса на надгробном памятнике |
|
| Мифология: | Древнегреческая мифология |
| Толкование имени: | Время |
| Занятие: | Олицетворение времени |
| Отец: | Хор |
| Дети: | Эфир, Хаос, Эреб |
| Место погребения: | Бессмертен. |
| Иллюстрации на Викискладе? | |
Хронос (др.-греч. Χρόνος, «время») — божество в древнегреческой мифологии и теокосмогонии[1][2]. Действует в орфической теогонии, порождает Эфир, Хаос и Эреб. У орфиков Нестареющий Хронос именуется также Гераклом и Драконом-Змеем[3]. Упомянут в орфическом гимне к Мусею (ст. 29).
По Ферекиду Сирскому, Хронос — одно из трёх первоначал, создал из своего семени огонь, пневму и воду[4]. Отец Хор[5].
По одному из описаний, Хаос породил самое древнее, что было в нашей зачинающейся Вселенной — Время. Эллины звали его Хронос. И теперь уже всё происходило во времени, так как пространство ещё только зарождалось. Хронос породил три стихии — Огонь, Воздух и Воду. Но это уже после того, как появилась Земля[6].
Позднее отождествлялся с Кроносом[7][8][9] на основании созвучия имён.
Мифическая космогония[править | править вики-текст]
В орфической космогонии, Хронос порождает Эфира и Хаоса и делает из них серебряное яйцо. Из него вышел перворожденный из боговФанет (другие имена его — Эрот, Метис, Эрикапей), который родил первое поколение богов.
Ферекид Сиросский, автор Семикнижия, признавал вечность начальной троицы богов: Заса (Зевса — эфир), Хтонии (хаос, подземные глубины) и Хроноса (время). Семя Хроноса было помещено в тайнике, из которого производится первое поколение богов.[10]
В современной культуре[править | править вики-текст]
- В японско-французском анимационном научно-фантастическом телесериале Ulysses 31 Хронос надеется использовать в качестве переключателя Улиссей, чтобы войти снова в мир богов.
- В видео-игре Heroes of Newerth Хронос является одним из видов порождений ада (Hellbourne), который умеет управлять временем и имеет навыки, которые могут сделать его одним из самых мощных, опасных и неуловимых героев в игре.
- В седьмом сезоне двенадцатого эпизода в сериале Сверхъестественное, Дин путешествует во времени, отправляется в 1944 год и охотится за Хроносом вместе с известным Элиотом Нессом.
- В короткометражном фильме Диснея Destino Хронос влюбляется в смертную женщину.[11]
- В Сейлор Мун Хронос является отцом Сейлор Плутона.
- В «Persona 2: Невинный Грех» Хронос — это персона Дзюна Куросу.
- В игре Анабиоз: Сон разума Хронос выступает в качестве финального босса.
- В романе Пирса Энтона «Властью песочных часов» Хронос — это «мантия», свалившаяся на главного героя, Нортона, и он живет своей жизнью, откатываясь во времени.
- Хронос — один из играбельных персонажей в игре Smite.
- В книжной серии «Бессмертные Секреты Николя Фламеля» Хронос появляется как старейшина, который может путешествовать во времени.
- В DC Comics, имя Хронос использовалось двумя разными персонажами. Первым был преступник, который пользовался своими часами как оружием, так и для показа трюков. Вторым был путешественником во времени, который защищал временную линию во Вселенной DC.
- Хронос появлялся в мультсериале Гриффины, в серии "Три стихийных бедствия" (12 сезон, 13 эпизод). Когда Питер Гриффин, Глен Квагмаер, Кливлинд Браун, и Джо Суонсон искали Бога, они пришли на гору Олимп, где встретили Хроноса. Хронос вручил Питеру подарочную корзинку.
Примечания[править | править вики-текст]
- ↑ Пиндар. Олимпийские песни, II, 19
- ↑ Мелеагр. Эпиграмма 5 Пейдж
- ↑ Орфика, фр. 54, 57 Керн
- ↑ Ферекид Сиросский, фр. В1 Дильс-Кранц
- ↑ См. Нонн. Деяния Диониса, II, 422
- ↑ Кун Н. А. «Легенды и мифы Древней Греции»
- ↑ Апион у Климента Римского. Гомилии VI 5 = Орфика, фр. 56 Керн
- ↑ Цицерон. О природе богов II 64
- ↑ Плутарх. Римские вопросы 12
- ↑ G. S. Kirk, J. E. Raven and M. Schofield The Presocratic Philosophers. — Cambridge University Press, 2003. — P. 24, 56.
- ↑ «Destino» by disney and Dali
|
[показать] |
|---|
|
-- Карты Зенера -- |
Карты Зенера
Карты Зе́нера, Зенеровские карты — колода карт с пятью повторяющимися рисунками (круг, крест, три волнистые линии, квадрат, пятиконечная звезда), предложенная в 1930-х годах психологом Карлом Зенером (англ. Karl Edward Zener) для изученияпаранормальных форм восприятия или способностей человека, например ясновидения.
Содержание
[убрать]
История возникновения[править | править вики-текст]
На первых этапах, для проведения так называемых исследований, использовалась обыкновенная игральная колода. Однако, у этого метода было множество недостатков. Например, для того чтобы верно ответить какая выпала карта, нужно было не только правильно назвать масть, но и её достоинство. Это в свою очередь означало, что шансы на верный ответ были очень невелики. Другая проблема заключалась в том, что испытуемые часто отдавали предпочтение какой-то одной карте, масти, или достоинству, и «предсказывали» выпадение именно этой карты, что сбивало эксперимент.
Чтобы избежать описанных выше недостатков, Карл Зенер предложил использовать свою колоду. В ней всего 25 карт, пять карт каждой разновидности: круг (одна сомкнутая линия), крест (две перекрещенные линии), три волнистые линии, квадрат (четыре линии), пятиконечная звезда[1].
Экспериментальное использование[править | править вики-текст]
При проведении опыта, экспериментатор использует хорошо перетасованную колоду, вытягивает одну из карт, записывая ответ подопытного. Тестируемый должен правильно определить символ изображённый на отобраной карте. Эксперимент продолжается до тех пор, пока не закончится колода.
Часто при проведении присутствует сторонний наблюдатель, который следит за чистотой эксперимента. Иногда тестируемый может быть помещён в отдельную комнату, чтобы предотвратить возможные преднамеренные или непреднамеренные подсказки со стороны проводящего испытание.
Если при проведении эксперимента результат (верно/неверно) сообщается испытуемому непосредственно после ответа, существует вероятность использования им метода «карточного подсчёта». При использовании этой стратегии, человек просчитывает вероятность выпадения той или иной карты, используя информацию о уже выпавших комбинациях. Также на точность эксперимента может повлиять плохо перетасованная колода.
На сегодняшний день разработаны онлайн-версии карт Зенера[2].
Толкование результатов теста[править | править вики-текст]
В качестве нулевой выбрали гипотезу, считающую, что в том случае, если карты из колоды выпадают абсолютно случайным образом, человек, не обладающий никакими паранормальными способностями, угадает верно примерно 20 процентов колоды (каждую пятую карту). Предполагается, что чем выше процент угаданных карт, тем большая вероятность того, что испытуемый обладает «особыми» способностями.
См. также[править | править вики-текст]
Ссылки[править | править вики-текст]
- Кэрролл Р. Т. Zener ESP cards // the Skeptic Dictionary или Энциклопедия заблуждений.
|
*** ЦИТАТА *** |
|
Понравилось: 2 пользователям
Уравнение Шрёдингера |
Уравнение Шрёдингера
|
|
|||||||||
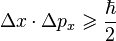 |
|||||||||
| Принцип неопределённости | |||||||||
|
Введение Математические основы |
|||||||||
|
|||||||||
| См. также: Портал:Физика |
Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве (в общем случае, в конфигурационном пространстве) и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике. Установлено Эрвином Шрёдингером в 1925 году, опубликовано в 1926 году.
Уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. В случае быстрых частиц и частиц со спином используются его обобщения (уравнение Клейна — Гордона, уравнение Паули, уравнение Дирака и др.)
В начале XX века учёные пришли к выводу, что между предсказаниями классической теории и экспериментальными данными об атомной структуре существует ряд расхождений. Открытие уравнения Шрёдингера последовало за революционным предположением де Бройля, что не только свету, но и вообще любым телам (в том числе и любым микрочастицам) присущи волновые свойства.
Исторически окончательной формулировке уравнения Шрёдингера предшествовал длительный период развития физики. Оно является одним из важнейших уравнений физики, объясняющих физические явления. Квантовая теория, однако, не требует полного отказа от законов Ньютона, а лишь определяет границы применимости классической физики. Следовательно, уравнение Шрёдингера должно согласовываться с законами Ньютона в предельном случае.
Содержание
[убрать]
Зависимое от времени уравнение[править | править вики-текст]
Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени[1] :
-
Зависимое от времени уравнение (общий случай) 
-
-
-
где
 — гамильтониан.
— гамильтониан.
-
где
-
Пример нерелятивистского уравнения Шрёдингера в координатном представлении для точечной частицы массы  , движущейся в потенциальном поле c потенциалом
, движущейся в потенциальном поле c потенциалом  :
:
-
Зависящее от времени уравнение Шрёдингера ![i\hbar\frac{\partial}{\partial t} \Psi(\vec{r} ,t) = \left [ -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r},t)\right ] \Psi(\vec{r} ,t)](https://upload.wikimedia.org/math/2/d/4/2d4f51c0eaecc66dbfb18fc887f711de.png)
Оператор  называется оператором Шредингера.
называется оператором Шредингера.
Формулировка[править | править вики-текст]
Общий случай[править | править вики-текст]
В квантовой физике вводится комплекснозначная функция  , описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.
, описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.
Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения  в частных физических задачах. Таким уравнением является уравнение Шрёдингера.
в частных физических задачах. Таким уравнением является уравнение Шрёдингера.
Пусть волновая функция задана в n-мерном конфигурационном пространстве, тогда в каждой точке с координатами  , в определенный момент времени t она будет иметь вид
, в определенный момент времени t она будет иметь вид  . В таком случае уравнение Шрёдингера запишется в виде:
. В таком случае уравнение Шрёдингера запишется в виде:

где 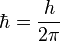 ,
,  — постоянная Планка;
— постоянная Планка;  — масса частицы,
— масса частицы,  — внешняя по отношению к частицепотенциальная энергия в точке
— внешняя по отношению к частицепотенциальная энергия в точке  в момент времени
в момент времени  ,
,  — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:

Случай трёхмерного пространства[править | править вики-текст]
В трёхмерном случае пси-функция является функцией трёх координат и  в декартовой системе координат заменяется выражением
в декартовой системе координат заменяется выражением

тогда уравнение Шрёдингера примет вид:
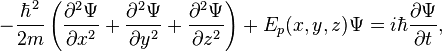
где 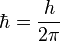 ,
,  — постоянная Планка;
— постоянная Планка;  — масса частицы,
— масса частицы,  — потенциальная энергия в точке
— потенциальная энергия в точке  .
.
Стационарное уравнение Шрёдингера[править | править вики-текст]
Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда  не является функцией времени, можно записать в виде:
не является функцией времени, можно записать в виде:

где функция  должна удовлетворять уравнению:
должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для  (2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).
(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).
Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции  от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции
от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции  совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции
совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции  .
.
Важное значение имеет интерпретация величины  в уравнении (2). Она производится следующим путём: временна́я зависимость функции
в уравнении (2). Она производится следующим путём: временна́я зависимость функции  в уравнении (2) имеет экспоненциальный характер, причём коэффициент при
в уравнении (2) имеет экспоненциальный характер, причём коэффициент при 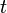 в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель
в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель . В левой же части уравнения (3) функция
. В левой же части уравнения (3) функция  умножается на потенциальную энергию
умножается на потенциальную энергию  . Следовательно, из соображений размерности вытекает, что величина
. Следовательно, из соображений размерности вытекает, что величина  должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что
должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что  представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера,
представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера,  действительно является полной энергией частицы при движении, описываемом функцией
действительно является полной энергией частицы при движении, описываемом функцией  .
.
Литература[править | править вики-текст]
- Березин Ф. А., Шубин М. А. Уравнение Шредингера. М.: Изд-во МГУ, 1983. 392с.
|
Принцип неопределённости Гейзенбе́рга |
Принцип неопределённости
|
|
|||||||||
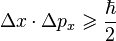 |
|||||||||
| Принцип неопределённости | |||||||||
|
Введение Математические основы |
|||||||||
|
|||||||||
| См. также: Портал:Физика |
Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемыхнекоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределённостей[ 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики.
Содержание
[убрать]
Краткий обзор[править | править вики-текст]
Соотношения неопределённостей Гейзенберга являются теоретическим пределом точности одновременных измерений двух некоммутирующих наблюдаемых. Они справедливы как для идеальных измерений, иногда называемых измерениями фон Неймана, так и для неидеальных измерений.[ 2]
Согласно принципу неопределённости у частицы не могут быть одновременно точно измерены положение и скорость (импульс)[ 3]. Принцип неопределённости уже в виде, первоначально предложенном Гейзенбергом, применим и в случае, когда не реализуется ни одна из двух крайних ситуаций (полностью определенный импульс и полностью неопределенная пространственная координата — или полностью неопределенный импульс и полностью определенная координата).
Пример: частица с определённым значением энергии, находящаяся в коробке с идеально отражающими стенками; она не характеризуется ни определённым значением импульса (учитывая его направление![ 4]), ни каким-либо определённым «положением» или пространственной координатой (волновая функция частицы делокализована на всё пространство коробки, то есть её координаты не имеют определенного значения, локализация частицы осуществлена не точнее размеров коробки).
Соотношения неопределённостей не ограничивают точность однократного измерения любой величины (для многомерных величин тут подразумевается в общем случае только одна компонента). Если её операторкоммутирует сам с собой в разные моменты времени, то не ограничена точность и многократного (или непрерывного) измерения одной величины. Например, соотношение неопределённостей для свободной частицы не препятствует точному измерению её импульса, но не позволяет точно измерить её координату (это ограничение называется стандартный квантовый предел для координаты).
Соотношение неопределенностей в квантовой механике в математическом смысле есть прямое следствие некоего свойства преобразования Фурье[ 5].
Существует точная количественная аналогия между соотношениями неопределённости Гейзенберга и свойствамиволн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может одновременно иметь и точное значение времени его фиксации, как его имеет очень короткий импульс, и точного значения частоты, как это имеет место для непрерывного (и в принципе бесконечно длительного) чистого тона (чистой синусоиды). Временно́е положение и частота волны математически полностью аналогичны координате и (квантово-механическому) импульсу частицы. Что совсем не удивительно, если вспомнить, что  , то есть импульс в квантовой механике — это и есть пространственная частота вдоль соответствующей координаты.
, то есть импульс в квантовой механике — это и есть пространственная частота вдоль соответствующей координаты.
В повседневной жизни мы обычно не наблюдаем квантовую неопределённость потому, что значение  чрезвычайно мало, и поэтому соотношения неопределенностей накладывают такие слабые ограничения на погрешности измерения, которые заведомо незаметны на фоне реальных практических погрешностей[ 6] наших приборов или органов чувств.
чрезвычайно мало, и поэтому соотношения неопределенностей накладывают такие слабые ограничения на погрешности измерения, которые заведомо незаметны на фоне реальных практических погрешностей[ 6] наших приборов или органов чувств.
Определение[править | править вики-текст]
Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения  координаты и среднеквадратического отклонения
координаты и среднеквадратического отклонения 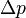 импульса, мы найдем что:
импульса, мы найдем что:
-
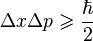 ,
,
где ħ — приведённая постоянная Планка.
Отметим, что это неравенство даёт несколько возможностей — состояние может быть таким, что  может быть измерен с высокой точностью, но тогда
может быть измерен с высокой точностью, но тогда  будет известен только приблизительно, или наоборот
будет известен только приблизительно, или наоборот  может быть определён точно, в то время как
может быть определён точно, в то время как  — нет. Во всех же других состояниях и
— нет. Во всех же других состояниях и  , и
, и  могут быть измерены с «разумной» (но не произвольно высокой) точностью.
могут быть измерены с «разумной» (но не произвольно высокой) точностью.
Варианты и примеры[править | править вики-текст]
Обобщённый принцип неопределённости[править | править вики-текст]
Принцип неопределённости не относится только к координате и импульсу (как он был впервые предложен Гейзенбергом). В своей общей форме он применим к каждой паре сопряжённых переменных. В общем случае, и в отличие от случая координаты и импульса, обсуждённого выше, нижняя граница произведения «неопределённостей» двух сопряжённых переменных зависит от состояния системы. Принцип неопределённости становится тогда теоремой в теории операторов, которая будет приведена далее.
Теорема. Для любых самосопряжённых операторов:  и
и  , и любого элемента
, и любого элемента  из
из  такого, что
такого, что 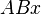 и
и 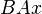 оба определены (то есть, в частности,
оба определены (то есть, в частности,  и
и 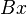 также определены), имеем:
также определены), имеем:
Это прямое следствие неравенства Коши — Буняковского.
Следовательно, верна следующая общая форма принципа неопределённости, впервые выведенная в 1930 г. Говардом Перси Робертсоном и (независимо) Эрвином Шрёдингером:
Это неравенство называют соотношением Робертсона — Шрёдингера.
Оператор  называют коммутатором
называют коммутатором  и
и  и обозначают как
и обозначают как ![[A,B]](https://upload.wikimedia.org/math/6/c/0/6c05dc26810646388d97a955bb009058.png) . Он определен для тех
. Он определен для тех  , для которых определены оба
, для которых определены оба 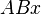 и
и 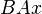 .
.
Из соотношения Робертсона — Шрёдингера немедленно следует соотношение неопределённости Гейзенберга:
Предположим,  и
и  — две физические величины, которые связаны с самосопряжёнными операторами. Если
— две физические величины, которые связаны с самосопряжёнными операторами. Если 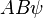 и
и  определены, тогда:
определены, тогда:
-
![\Delta_{\psi}A\,\Delta_{\psi}B \geqslant \frac{1}{2}\left|\left\langle\left[A,{B}\right]\right\rangle_\psi\right|](https://upload.wikimedia.org/math/4/4/a/44aa446ee798a9915dcb3897ba286480.png) ,
,
где:
— среднее значение оператора величины  в состоянии
в состоянии  системы, и
системы, и
— оператор стандартного отклонения величины  в состоянии
в состоянии  системы.
системы.
Приведённые выше определения среднего и стандартного отклонения формально определены исключительно в терминах теории операторов. Утверждение становится однако более значащим, как только мы заметим, что они являются фактически средним и стандартным отклонением измеренного распределения значений. См. квантовая статистическая механика.
То же самое может быть сделано не только для пары сопряжённых операторов (например координаты и импульса, или продолжительности и энергии), но вообще для любой пары Эрмитовых операторов. Существует отношение неопределённости между напряжённостью поля и числом частиц, которое приводит к явлению виртуальных частиц.
Возможно также существование двух некоммутирующих самосопряжённых операторов  и
и  , которые имеют один и тот же собственный вектор
, которые имеют один и тот же собственный вектор  . В этом случае
. В этом случае  представляет собой чистое состояние, которое является одновременно измеримым для
представляет собой чистое состояние, которое является одновременно измеримым для  и
и  .
.
Общие наблюдаемые переменные, которые подчиняются принципу неопределённости[править | править вики-текст]
Предыдущие математические результаты показывают, как найти соотношения неопределённостей между физическими переменными, а именно, определить значения пар переменных  и
и  , коммутатор которых имеет определённые аналитические свойства.
, коммутатор которых имеет определённые аналитические свойства.
- самое известное отношение неопределённости — между координатой и импульсом частицы в пространстве:
- отношение неопределённости между двумя ортогональными компонентами оператора полного углового момента частицы:
-

-
где


 различны и
различны и 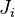 обозначает угловой момент вдоль оси
обозначает угловой момент вдоль оси  .
.
- следующее отношение неопределённости между энергией и временем часто представляется в учебниках физики, хотя его интерпретация требует осторожности, так как не существует оператора, представляющего время:
Здесь 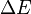 - неопределенность изменения энергии системы,
- неопределенность изменения энергии системы,  - длительность измерения. Единого мнения о выводимости этого соотношения из остальных аксиом квантовой механики нет.[1]
- длительность измерения. Единого мнения о выводимости этого соотношения из остальных аксиом квантовой механики нет.[1]
|
Процитировано 1 раз
Сила Лоренца |
Сила Лоренца
|
|
||||||
 |
||||||
| Электричество · Магнетизм | ||||||
|
||||||
| См. также: Портал:Физика |
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью  заряд
заряд 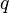 лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороныэлектрического
лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороныэлектрического  и магнитного
и магнитного  полей. В Международной системе единиц (СИ)выражается как:
полей. В Международной системе единиц (СИ)выражается как:
![\mathbf{F}=q\left(\mathbf{E}+[\mathbf{v}\times\mathbf{B}]\right)](https://upload.wikimedia.org/math/f/7/1/f7114c785dae4f1e11bd46a650a45625.png)
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца[3].
Содержание
[убрать]
Уравнение (единицы СИ)[править | править вики-текст]
Заряженная частица[править | править вики-текст]
Сила F, действующая на частицу с электрическим зарядом q, движущуюся со скоростью v, во внешнем электрическом E и магнитном B полях, такова:
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда[править | править вики-текст]
Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись[править | править вики-текст]
4-сила выражается через вектор 4-скорости частицы по формуле
-
 , где
, где  — 4-сила, q — заряд частицы,
— 4-сила, q — заряд частицы,  — тензор электромагнитного поля,
— тензор электромагнитного поля,  — 4-скорость.
— 4-скорость.
Частные случаи[править | править вики-текст]
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса  (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
(называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
|
|
|
|---|---|
|
|
|
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости 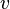 , намного меньшей скорости света, круговая частота
, намного меньшей скорости света, круговая частота 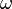 не зависит от
не зависит от 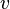 :
:
|
|
|
|---|---|
|
|
|
Если заряженная частица движется в магнитном поле так, что вектор скорости 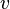 составляет с вектором магнитной индукции
составляет с вектором магнитной индукции  угол
угол  , то траекторией движения частицы является винтовая линия с радиусом
, то траекторией движения частицы является винтовая линия с радиусом  и шагом винта
и шагом винта  :
:
| СГС | СИ |
|---|---|
|
|
Использование[править | править вики-текст]
- В электроприборах
Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины(электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД-генераторах.
- В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
- В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
- Другие применения
- Бесконтактное измерение скорости движения проводящей жидкости (Велосиметрия силой Лоренца).
См. также[править | править вики-текст]
Ссылки[править | править вики-текст]
|
Три закона Артура Кларка |
|
Процитировано 1 раз
Понравилось: 1 пользователю
Фатимские пророчества |

Фатимские пророчества
В мае 2000 года Ватикан, наконец, обнародовал долгожданное третье пророчество Фатимы. Некоторые верующие испытали облегчение, однако многие были разочарованы – они ожидали большего.
«Чудо в Фатиме» — самое известное явление Божьей Матери. Ее явление трем детям-пастушкам в деревушке Фатима, Португалия, в 1917 году, по свидетельству многих очевидцев, сопровождалось рядом необъяснимых явлений, в том числе
беспорядочным перемещением солнца по небу. О небывалой «пляске солнца», свидетелями которой стали не менее пятидесяти тысяч людей, сообщили все значительные лиссабонские газеты.
Во время общения с детьми Дева Мария сообщила им три тайны, три откровения. Первые два пророчества были обнародованы Люцией дос Сантос, старшей из троих детей, в начале 1940 года, но третье и последнее пророчество должно было оставаться скрытым до 1960 года. Но 1960 прошел, а третье пророчество Фатимы так и не было обнародовано, так как Ватикан заявил, что мир к нему не совсем готов. Это нежелание раскрыть секрет привело к спекуляции среди верующих, что пророчество содержит информацию о нашем будущем, которое настолько ужасно, что Папа не смеет показать это. Возможно, третье фатимское пророчество предрекает ядерную войну… или конец света?
Первое пророчество Фатимы
В первом откровении детям были показаны страшные видения ада, в который «отправляются души бедных грешников». Затем Богородица обратилась к детям с такими словами: «Война (Первая мировая война) идет к концу, но если люди не прекратят оскорблять Бога, то начнется другая, еще хуже, во времена Пия… Когда вы увидите, что ночная тьма осветилась таинственным светом, как днем, знайте, что это великое знамение дано вам от Бога, что Он собирается наказать мир за его преступления посредством войны, голода и гонений на Церковь и Святейшего Отца…».
Помогло ли это пророчество? Первая мировая война в самом деле скоро закончилась, и действительно началась другая, еще хуже, — Вторая мировая война. Но помните, что Люция обнародовала это пророчество в письменной форме лишь в 1940 году, то есть уже после начала Второй мировой войны. Кроме того, любопытно, что в пророчестве прямо называется Пий XI. В 1917 году, когда произошло явление Богородицы и было дано первое пророчество, папский престол занимал Бенедикт XV. Пий XI стал Папой в 1922 году. Так что или Богородица предсказала и имя будущего Папы, который занимал папский престол до 1939 года, или Люция добавила немного от себя.
Что можно сказать о знамении, когда «ночная тьма осветилась светом, как днем», которое должно было возвестить начало войны? По некоторым данным, 25 января 1938 года, за год до начала Второй мировой войны, на всей территории Европы наблюдалось замечательное явление – северное сияние. Это сияние наблюдалось даже на юге Европы – в Галисии, Испания, где в это время проживала сестра Люция, единственная оставшаяся в живых из очевидцев явления Пресвятой Девы (Франциско и Хиацинта заболели испанкой и умерли: Франциско умер в 1919 году в возрасте 10 лет, а Хиацинта – в 1920 году в возрасте 9 лет). Люция сразу же увидела в северном сиянии то самое предзнаменование, о котором говорилось в первом пророчестве. Это необъяснимое северное сияние над Европой видел даже Пий XI в Ватикане. Кроме того, по воспоминаниям очевидцев, сияние сопровождалось странным «треском», который мог быть вызван с разрядами электричества в атмосфере. Во многих регионах Европы началась паника, так как население решило, что мир охвачен огнем, и что пришел конец света.Хотя северное сияние и выглядело очень эффектно, даже в 1917 году его нельзя было назвать «таинственным светом». Кроме того, не будем забывать, что Люция обнародовала это пророчество уже после того, как факт свершился – Вторая мировая началась.
Второе пророчество Фатимы
«Когда вы увидите, что ночная тьма осветилась таинственным светом, как днем, знайте, что это великое знамение дано вам от Бога, что Он собирается наказать мир за его преступления… Чтобы не допустить этого, Я пришла просить у вас посвящения России Моему Сердцу и искупительных причастий каждую первую субботу месяца. Если прислушаются к Моей просьбе и Россия будет обращена к Богу, наступит мир. Если опять не внемлют, она распространит свои ошибки по всему миру, вызывая войны и преследования Церкви… Нечестие распространится по всей земле, многие народы будут уничтожены…».Когда вы видите ночью освещенные неизвестный свет, знаю, что это великий знак дал вам Бог, что он собирается наказать мир. Чтобы предотвратить это, я приду просить о посвящении России в Мое Непорочное Сердце, а причастие возмещения на Первом по субботам [каждого месяца] Если мои просьбы услышаны, Россия будет преобразована, и будет мир; если нет, то она будет распространять свои ошибки по всему миру, вызывая войны и гонения Церкви. Праведники примут мученическую смерть, а Святой Отец будет много страдать, целые народы будут уничтожены…».
Многие верующие утверждают, что это пророчество предусматривает распространение коммунизма по всему мира из России, которая стала Советским Союзом. Конечно, войны велись, чтобы остановить распространение коммунизма. Затем в 1984 году Папа Иоанн Павел II посвятил Советский Союз Богоматери и несколько лет спустя, в 1991 году, Советский Союз распался на 15 независимых государств, хотя вряд ли можно сказать, что Россия прошла посвящение и преобразование. Воцарился ли мир, как было предсказано? Хотя мировых войн больше не было, на Востоке не прекращаются «военные конфликты», в которых гибнут тысячи людей. В мире все еще неспокойно.
Нам остается только принимать на веру точность первых двух пророчеств Фатимы. Скептики могут найти в них множество несоответствий, однако верующие считают их доказательством того, что небеса не безразличны к живущим на Земле. Но каково же третье пророчество, которого все так ожидали и боялись?
Третье пророчество Фатимы
В 1944 году Люция изложила на бумаге третье пророчество, которое, по ее словам, она услышала в 1917 году, когда ей было всего 10 лет. Сестра Люция (повзрослев, она стала монахиней) запечатала письмо и оправила его португальскому епископу Лейрии. Она сказала ему, что третье откровение Богородицы может быть открыто миру не ранее 1960 года. Епископ передал пророчество в Ватикан. В 1960 году Павел Иоанн XXIII вскрыл запечатанное пророчество и прочитал его, а верующие всего мира с нетерпением ожидали обещанного откровения. Но этому не суждено было случиться. Вопреки велению Пресвятой Богородицы, Папа отказался раскрыть содержание пророчества, мотивируя это тем, что «пророчество не относится к моему времени». По слухам, Иоанн XXIII упал в обморок, когда прочел третий секрет Фатимы, потому что, как рассказывают те, кто видел текст пророчества своими глазами, в нем говорится, что Папа предаст свою паству и отправит ее на бойню, уготованную самим Люцифером. Иоанн XXIII упал в обморок, потому что думал, что именно он станет Папой, который откроет дверь для сатаны, и что ему суждено Антипапой, о котором говорят и другие пророчества.
Предполагают, что последующие Папы также ознакомились с третьим откровением и также решили не обнародовать его. И вот в 2000 году, 40 лет спустя, полный текст пророчества был наконец опубликован, но споры вокруг него не утихают и сегодня, двенадцать лет спустя.
13 мая 2000 года, в день 83-летия первого явления Фатимской Богоматери, Иоанн Павел II посетил храм в Фатиме и сделал неожиданное заявление о том, что не видит более необходимости хранить тайну третьего пророчества. Ватикан рассказал миру, что в откровении было предсказано покушение на Папу Иоанна Павла II, совершенное турецким террористом Али Агджой 13 мая 1981 года.
|
Понравилось: 2 пользователям
ТАЛИСМАНЫ И ОМУЛЕТЫ |
00
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

|
Понравилось: 6 пользователям
Художник Johannes Wessmark |
http://subscribe.ru/group/nash-soyuz/5901997/
http://www.risunoc.com/2012/12/johannes-wessmark-sovremennyy.html
http://art-links.livejournal.com/2471148.html
Если бог нас своим могуществом
После смерти отправит в рай,
Что мне делать с земным имуществом,
Если скажет он: выбирай?
Мне не надо в раю тоскующей,
Чтоб покорно за мною шла,
Я бы взял с собой в рай такую же,
Что на грешной земле жила,-
Злую, ветреную, колючую,
Хоть ненадолго, да мою!
Ту, что нас на земле помучила
И не даст нам скучать в раю.
В рай, наверно, таких отчаянных
Мало кто приведёт с собой,
Будут праведники нечаянно
Там подглядывать за тобой.
Взял бы в рай с собой расстояния,
Чтобы мучиться от разлук,
Чтобы помнить при расставании
Боль сведённых на шее рук.
Взял бы в рай с собой всё опасности,
Чтоб вернее меня ждала,
Чтобы глаз своих синей ясности
Дома трусу не отдала.
Взял бы в рай с собой друга верного,
Чтобы было с кем пировать,
И врага, чтоб в минуту скверную
По-земному с ним враждовать.
Ни любви, ни тоски, ни жалости,
Даже курского соловья,
Никакой, самой малой малости
На земле бы не бросил я.
Даже смерть, если б было мыслимо,
Я б на землю не отпустил,
Всё, что к нам на земле причислено,
В рай с собою бы захватил.
И за эти земные корысти,
Удивлённо меня кляня,
Я уверен, что бог бы вскорости
Вновь на землю столкнул меня.
Константин Симонов

Художник фотореалист Johannes Wessmark родился в 1962 году, живет и работает в Kil, Швеция. Профессионального художественного образования не получал, но если в его руки попадает карандаш или кисть с акварельной краской, можно быть уверенными в том, что на полотне в скором времени появится шедевр. Более пятнадцати лет работал в качестве иллюстратора и 3D художником. Член The Swedish Artists National Organisation и International Guild of Realism. Его картины представлены в художественных выставках по всей Швеции и США.






















|
Процитировано 3 раз
Понравилось: 5 пользователям



















































































































































































































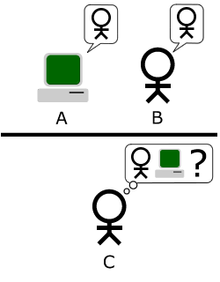






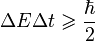










 ,
,
 ,
,










