[»з песочницы] арта самоорганизации (Self-orginizing map) на TensorFlow |
ѕривет, ’абр! Ќедавно начал свое знакомство с библиотекой глубокого обучени€ (Deep Learning) от Google под названием TensorFlow. » захотелось в качестве эксперимента написать карту самоорганизации охонена. ѕоэтому решил зан€тьс€ ее созданием использу€ стандартный функционал данной библиотеки. ¬ статье описано что из себ€ представл€ет карта самоорганизации охонена и алгоритм ее обучени€. ј также приведен пример ее реализации и что из этого всего вышло.

ƒл€ начала разберемс€ что из себ€ представл€ет карта самоорганизации (Self-orginizing Map), или просто SOM. SOM Ц это искусственна€ нейронна€ сеть основанна€ на обучении без учител€. ¬ картах самоорганизации нейроны помещени в узлах решетки, обычно одно- или двумерной. ¬се нейроны этой решетки св€заны со всеми узлами входного сло€.

SOM преобразует непрерывное исходное пространство в дискретное выходное пространство .
ќбучение сети состоит из трех основных процессов: конкуренци€, коопераци€ и адаптаци€. Ќиже описаны все шаги алгоритма обучени€ SOM.
Ўаг 1: »нициализаци€. ƒл€ всех векторов синаптических весов,где Ч общее количество нейронов, Ч размерность входного пространства, выбираетс€ случайное значение от -1 до 1.
Ўаг 2: ѕодвыборка. ¬ыбираем вектор из входного пространства.
Ўаг 3: ѕоиск победившего нейрона или процесс конкуренции. Ќаходим наиболее подход€щий (победивший нейрон) на шаге , использу€ критерий минимума ≈вклидова рассто€ни€ (что эквивалентно максимуму скал€рных произведений ):
Ўаг 4: ѕроцесс кооперации. Ќейрон-победитель находитс€ в центре топологической окрестности Ђсотрудничающихї нейронов. лючевой вопрос: как определить так называемую топологическую окрестность (topological neighbourhood) победившего нейрона? ƒл€ удобства обозначим ее символом: , с центром в победившем нейроне . “опологическа€ окрестность должна быть симметричной относительно точки максимума, определ€емой при , Ч это латеральное рассто€ние (lateral distance) между победившим и соседними нейронами .
“ипичным примером, удовлетвор€ющим условию выше, €вл€етс€ функци€ √аусса: где Ч эффективна€ ширина (effective width). Ћатеральное рассто€ние определ€етс€ как: в одномерном, и: в двумерном случае. √де определ€ет позицию возбуждаемого нейрона, а Ч позицию победившего нейрона (в случае двумерной решетки , где и координаты нейрона в решетке).
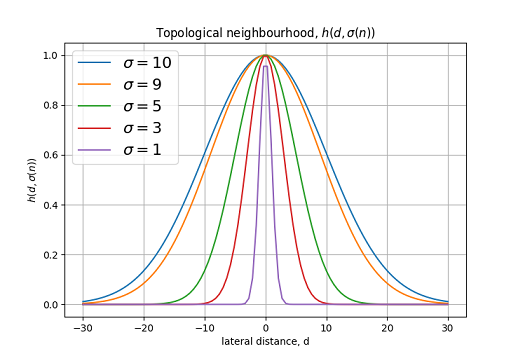
√рафик функции топологической окрестности дл€ различных .
ƒл€ SOM характерно уменьшение топологической окрестности в процессе обучени€. ƒостичь этого можно измен€€ по формуле: где Ч некотора€ константа, Ч шаг обучени€, Ч начальное значение .

√рафик изменением в процессе обучени€.
‘ункци€ по окончании этапа обучени€ должна охватывать только ближайших соседей. Ќа рисунках ниже приведены графики функции топологической окрестности дл€ двумерной решетки.
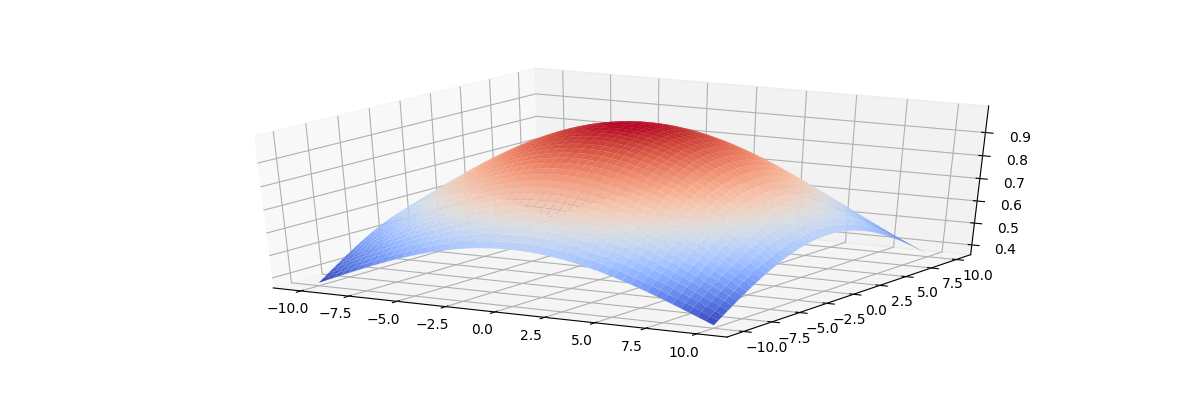
»з данного рисунка видно, что в начале обучени€ топологическа€ окрестность охватывает практически всю решетку.

¬ конце обучени€ сужаетс€ до ближайших соседей.
Ўаг 5: ѕроцесс адаптации. ѕроцесс адаптации включает в себ€ изменение синаптических весов сети. »зменение вектора весов нейрона в решетке можно выразить следующим образом: Ч параметр скорости обучени€.
¬ итоге имеем формулу обновленного вектора весов в момент времени :
¬ алгоритме обучени€ SOM также рекомендуетс€ измен€ть параметр скорости обучени€ в зависимости от шага.
где Ч еще одна константа алгоритма SOM.

√рафик изменением в процессе обучени€.
ѕосле обновлени€ весов возвращаемс€ к шагу 2 и так далее.
ќбучени€ сети состоит из двух этапов:
Ётап самоорганизации Ч может зан€ть до 1000 итерций а может и больше.
Ётап сходимости Ч требуетс€ дл€ точной подстройки карты признаков. ак правило, количесвто итераций, достаточное дл€ этапа сходимости может превышать количество нейоронов в сети в 500 раз.
Ёвристика 1. Ќачальное значение параметра скорости обучени€ лучше выбрать близким к значению: , . ѕри этом оно не должно опускатьс€ ниже значени€ 0.01.
Ёвристика 2. »сходное значение следует установить примерно равной радиусу решетки, а константу опрелить как: Ќа этапе сходимости следует остановить изменение .
“еперь перейдем от теории к практической реализации самоорганизующейс€ карты (SOM) с помощью Python и TensorFlow.
ƒл€ начала создадим класс SOMNetwork и создадим операции TensorFlow дл€ инициализации всех констант:
ƒалее создадим функцию дл€ создани€ операции процесса конкуренции:
Ќам осталось создать основную операцию обучени€ дл€ процессов кооперации и адаптации:
¬ итоге мы реализовали SOM и получили операцию training_op с помощью которой можно обучать нашу нейронную сеть, передава€ на каждой итерации входной вектор и номер шага как параметр. Ќиже приведен граф операций TensorFlow построенный с помощью Tesnorboard.
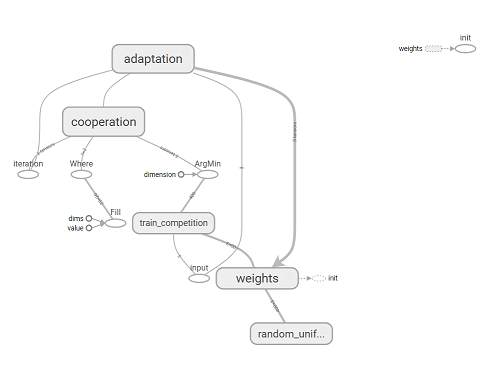
√раф операций TensorFlow.
ƒл€ тестировани€ работы программы, будем подавать на вход трехмерный вектор . ƒанный вектор можно представить как цвет из трех компонент.
—оздадим экземпл€р нашей SOM сети и массив из рандомных векторов (цветов):
“еперь можно реализовать основной цикл обучени€:
ѕосле обучени€ сеть преобразует непрерывное входное пространство цветов в дискретную градиентную карту, при подаче одной гаммы цветов всегда будут активироватьс€ нейроны из одной области карты соответствующей данному цвету (активируетс€ один нейрон наиболее подход€щий подаваемому вектору). ƒл€ демонстрации можно представить вектор синаптических весов нейронов как цветовое градиентное изображение.
Ќа рисунке представлена карта весов дл€ сети 20х20 нейронов, после 200тыс. итераций обучени€:
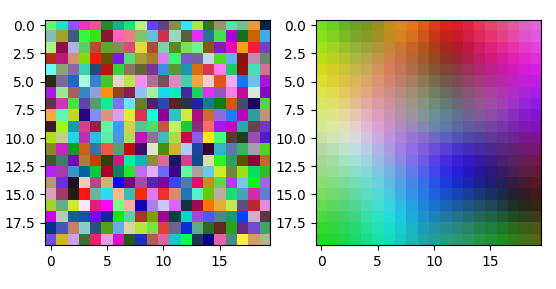
арта весов в начале обучени€ (слева) и в конце обучени€ (справа).

арта весов дл€ сети 100x100 нейронов, после 350тыс. итераций обучени€.
¬ итоге создана самоорганизующа€с€ карта и показан пример ее обучени€ на входном векторе состо€щим из трех компонент. ƒл€ обучени€ сети можно использовать вектор любой размерности. “ак же можно преобразовать алгоритм дл€ работы в пакетном режиме. ѕри этом пор€док представлени€ сети входных данных не вли€ет на окончательную форму карты признаков и нет необходимости в изменении параметра скорости обучени€ со временем.
P.S.: ѕолный код программы можно найти тут.
ћетки:
author M00nL1ght
машинное обучение
python
machine learning
tensorflow
neural networks

ќ картах самоорганизации
ƒл€ начала разберемс€ что из себ€ представл€ет карта самоорганизации (Self-orginizing Map), или просто SOM. SOM Ц это искусственна€ нейронна€ сеть основанна€ на обучении без учител€. ¬ картах самоорганизации нейроны помещени в узлах решетки, обычно одно- или двумерной. ¬се нейроны этой решетки св€заны со всеми узлами входного сло€.

SOM преобразует непрерывное исходное пространство в дискретное выходное пространство .
јлгоритм обучени€ SOM
ќбучение сети состоит из трех основных процессов: конкуренци€, коопераци€ и адаптаци€. Ќиже описаны все шаги алгоритма обучени€ SOM.
Ўаг 1: »нициализаци€. ƒл€ всех векторов синаптических весов,где Ч общее количество нейронов, Ч размерность входного пространства, выбираетс€ случайное значение от -1 до 1.
Ўаг 2: ѕодвыборка. ¬ыбираем вектор из входного пространства.
Ўаг 3: ѕоиск победившего нейрона или процесс конкуренции. Ќаходим наиболее подход€щий (победивший нейрон) на шаге , использу€ критерий минимума ≈вклидова рассто€ни€ (что эквивалентно максимуму скал€рных произведений ):
≈вклидово рассто€ние.
≈вклидово рассто€ние () определ€тс€ как:
Ўаг 4: ѕроцесс кооперации. Ќейрон-победитель находитс€ в центре топологической окрестности Ђсотрудничающихї нейронов. лючевой вопрос: как определить так называемую топологическую окрестность (topological neighbourhood) победившего нейрона? ƒл€ удобства обозначим ее символом: , с центром в победившем нейроне . “опологическа€ окрестность должна быть симметричной относительно точки максимума, определ€емой при , Ч это латеральное рассто€ние (lateral distance) между победившим и соседними нейронами .
“ипичным примером, удовлетвор€ющим условию выше, €вл€етс€ функци€ √аусса: где Ч эффективна€ ширина (effective width). Ћатеральное рассто€ние определ€етс€ как: в одномерном, и: в двумерном случае. √де определ€ет позицию возбуждаемого нейрона, а Ч позицию победившего нейрона (в случае двумерной решетки , где и координаты нейрона в решетке).

√рафик функции топологической окрестности дл€ различных .
ƒл€ SOM характерно уменьшение топологической окрестности в процессе обучени€. ƒостичь этого можно измен€€ по формуле: где Ч некотора€ константа, Ч шаг обучени€, Ч начальное значение .

√рафик изменением в процессе обучени€.
‘ункци€ по окончании этапа обучени€ должна охватывать только ближайших соседей. Ќа рисунках ниже приведены графики функции топологической окрестности дл€ двумерной решетки.

»з данного рисунка видно, что в начале обучени€ топологическа€ окрестность охватывает практически всю решетку.

¬ конце обучени€ сужаетс€ до ближайших соседей.
Ўаг 5: ѕроцесс адаптации. ѕроцесс адаптации включает в себ€ изменение синаптических весов сети. »зменение вектора весов нейрона в решетке можно выразить следующим образом: Ч параметр скорости обучени€.
¬ итоге имеем формулу обновленного вектора весов в момент времени :
¬ алгоритме обучени€ SOM также рекомендуетс€ измен€ть параметр скорости обучени€ в зависимости от шага.
где Ч еще одна константа алгоритма SOM.

√рафик изменением в процессе обучени€.
ѕосле обновлени€ весов возвращаемс€ к шагу 2 и так далее.
Ёвристики алгоритма обучени€ SOM
ќбучени€ сети состоит из двух этапов:
Ётап самоорганизации Ч может зан€ть до 1000 итерций а может и больше.
Ётап сходимости Ч требуетс€ дл€ точной подстройки карты признаков. ак правило, количесвто итераций, достаточное дл€ этапа сходимости может превышать количество нейоронов в сети в 500 раз.
Ёвристика 1. Ќачальное значение параметра скорости обучени€ лучше выбрать близким к значению: , . ѕри этом оно не должно опускатьс€ ниже значени€ 0.01.
Ёвристика 2. »сходное значение следует установить примерно равной радиусу решетки, а константу опрелить как: Ќа этапе сходимости следует остановить изменение .
–еализаци€ SOM с помощью Python и TensorFlow
“еперь перейдем от теории к практической реализации самоорганизующейс€ карты (SOM) с помощью Python и TensorFlow.
ƒл€ начала создадим класс SOMNetwork и создадим операции TensorFlow дл€ инициализации всех констант:
import numpy as np
import tensorflow as tf
class SOMNetwork():
def __init__(self, input_dim, dim=10, sigma=None, learning_rate=0.1, tay2=1000, dtype=tf.float32):
#если сигма на определена устанавливаем ее равной половине размера решетки
if not sigma:
sigma = dim / 2
self.dtype = dtype
#определ€ем константы использующиес€ при обучении
self.dim = tf.constant(dim, dtype=tf.int64)
self.learning_rate = tf.constant(learning_rate, dtype=dtype, name='learning_rate')
self.sigma = tf.constant(sigma, dtype=dtype, name='sigma')
#тау 1 (формула 6)
self.tay1 = tf.constant(1000/np.log(sigma), dtype=dtype, name='tay1')
#минимальное значение сигма на шаге 1000 (определ€ем по формуле 3)
self.minsigma = tf.constant(sigma * np.exp(-1000/(1000/np.log(sigma))), dtype=dtype, name='min_sigma')
self.tay2 = tf.constant(tay2, dtype=dtype, name='tay2')
#input vector
self.x = tf.placeholder(shape=[input_dim], dtype=dtype, name='input')
#iteration number
self.n = tf.placeholder(dtype=dtype, name='iteration')
#матрица синаптических весов
self.w = tf.Variable(tf.random_uniform([dim*dim, input_dim], minval=-1, maxval=1, dtype=dtype),
dtype=dtype, name='weights')
#матрица позиций всех нейронов, дл€ определени€ латерального рассто€ни€
self.positions = tf.where(tf.fill([dim, dim], True))
ƒалее создадим функцию дл€ создани€ операции процесса конкуренции:
def __competition(self, info=''):
with tf.name_scope(info+'competition') as scope:
#вычисл€ем минимум евклидова рассто€ни€ дл€ всей сетки нейронов
distance = tf.sqrt(tf.reduce_sum(tf.square(self.x - self.w), axis=1))
#возвращаем индекс победившего нейрона (формула 1)
return tf.argmin(distance, axis=0)
Ќам осталось создать основную операцию обучени€ дл€ процессов кооперации и адаптации:
def training_op(self):
#определ€ем индекс победившего нейрона
win_index = self.__competition('train_')
with tf.name_scope('cooperation') as scope:
#вычисл€ем латеральное рассто€ние d
#дл€ этого переводим инедкс победившего нейрона из 1d координаты в 2d координату
coop_dist = tf.sqrt(tf.reduce_sum(tf.square(tf.cast(self.positions -
[win_index//self.dim, win_index-win_index//self.dim*self.dim],
dtype=self.dtype)), axis=1))
#корректируем сигма (использу€ формулу 3)
sigma = tf.cond(self.n > 1000, lambda: self.minsigma, lambda: self.sigma * tf.exp(-self.n/self.tay1))
#вычисл€ем топологическую окрестность (формула 2)
tnh = tf.exp(-tf.square(coop_dist) / (2 * tf.square(sigma)))
with tf.name_scope('adaptation') as scope:
#обновл€ем параметр скорости обучени€ (формула 5)
lr = self.learning_rate * tf.exp(-self.n/self.tay2)
minlr = tf.constant(0.01, dtype=self.dtype, name='min_learning_rate')
lr = tf.cond(lr <= minlr, lambda: minlr, lambda: lr)
#вычисл€ем дельта весов и обновл€ем всю матрицу весов (формула 4)
delta = tf.transpose(lr * tnh * tf.transpose(self.x - self.w))
training_op = tf.assign(self.w, self.w + delta)
return training_op
¬ итоге мы реализовали SOM и получили операцию training_op с помощью которой можно обучать нашу нейронную сеть, передава€ на каждой итерации входной вектор и номер шага как параметр. Ќиже приведен граф операций TensorFlow построенный с помощью Tesnorboard.
√раф операций TensorFlow.
“естирование работы программы
ƒл€ тестировани€ работы программы, будем подавать на вход трехмерный вектор . ƒанный вектор можно представить как цвет из трех компонент.
—оздадим экземпл€р нашей SOM сети и массив из рандомных векторов (цветов):
#сеть размером 20х20 нейронов
som = SOMNetwork(input_dim=3, dim=20, dtype=tf.float64, sigma=3)
test_data = np.random.uniform(0, 1, (250000, 3))
“еперь можно реализовать основной цикл обучени€:
training_op = som.training_op()
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
for i, color_data in enumerate(test_data):
if i % 1000 == 0:
print('iter:', i)
sess.run(training_op, feed_dict={som.x: color_data, som.n:i})
ѕосле обучени€ сеть преобразует непрерывное входное пространство цветов в дискретную градиентную карту, при подаче одной гаммы цветов всегда будут активироватьс€ нейроны из одной области карты соответствующей данному цвету (активируетс€ один нейрон наиболее подход€щий подаваемому вектору). ƒл€ демонстрации можно представить вектор синаптических весов нейронов как цветовое градиентное изображение.
Ќа рисунке представлена карта весов дл€ сети 20х20 нейронов, после 200тыс. итераций обучени€:

арта весов в начале обучени€ (слева) и в конце обучени€ (справа).

арта весов дл€ сети 100x100 нейронов, после 350тыс. итераций обучени€.
«аключение
¬ итоге создана самоорганизующа€с€ карта и показан пример ее обучени€ на входном векторе состо€щим из трех компонент. ƒл€ обучени€ сети можно использовать вектор любой размерности. “ак же можно преобразовать алгоритм дл€ работы в пакетном режиме. ѕри этом пор€док представлени€ сети входных данных не вли€ет на окончательную форму карты признаков и нет необходимости в изменении параметра скорости обучени€ со временем.
P.S.: ѕолный код программы можно найти тут.
| омментировать | « ѕред. запись — дневнику — —лед. запись » | —траницы: [1] [Ќовые] |






