-÷итатник
‘асци€. —еть св€зующей все органы ткани. - (2)
‘асци€. “аинственный мир под кожей. ‘асци€. “аинственный мир под кожей. ¬идео. азалось бы, на...
ћы думаем, что видим мир чЄтко и в реальном времени, но зрение устроено иначе - (0)ћы думаем, что видим мир чЄтко и в реальном времени, но зрение устроено иначе «афиксируйте взг...
Ёфирна€ энерги€ Ц это ткань пространства - (0)Ёфирна€ энерги€ – это ткань пространства Ёфир и эфирна€ энерги€ - звучит как о...
‘изики открыли межвременные порталы - (0)‘изики открыли межвременные порталы ”ченые отказались от идеи путешествовать по...
»гра на троих: рестики-нолики-единички. - (0)»гра на троих: рестики-нолики-единички. —нова придумала игру на троих)) огда-то в 2016 го...
-ћетки
jyj Ўива агни адыги алексеев с.т артефакт асмик белогор брахма бурислав сервест викъ вишну вол€ врем€ выживание гласные глюоновые цепи голограмма горъ деревь€ дети днк догода другой мир душа женщина жизнь жыжъ звук звукова€ волна звукотерапи€ земл€ зеркало зеркальный мир иванова в. иегова информационный мир ириана карты кастанеда квантова€ механика кержаки космос кот кошка красота кристалл кротова€ дыра ланка ланкара лес луна любовь л€ 430 гц маги€ марийцы матрица меч михайлов к. мозг мо€ игра мужчина наблюдатель нить осознанное сновидение паразит переход позвоночник пришелец пространство пузырь алькубьерре путь п€тибрат в. разум рудра руны руны макоши руны рода руны руского рода руны русского рода руский род руский €зык русь свет св€щенна€ роща св€щенные деревь€ сила сказ как сказка сканда слепое п€тно слово смерть солнце спасЄм деревь€! спасем деревь€ староверы судьба телепортаци€ тримурти фоменко в.н. фотон футарк х.аргуэльес хима человек черкессы шаман шарова€ молни€ шелуд€ков а. электрон энерги€ эпифиз €зык
-–убрики
- "ƒоски —удьбы - ќктава ƒуши" (7)
- јлексеев —.“. (11)
- Ѕ.—ервест "ћаги€ Ѕессмерти€" (28)
- ¬.ѕ€тибрат "√лубинна€ книга" (25)
- ¬и ъ и √о –ъ - староверы, которые подарили –уны (67)
- ¬ыживание („еурин √.—. и другие) (18)
- деревь€ (54)
- ƒруиды, кельтские, ирландские традиции (36)
- жизнь (33)
- ∆ы ∆ъ (Jyj) (152)
- »з дневника "«вон –ун" (296)
- интересные книги и произведени€ (216)
- истори€ (58)
- артины ќктавестана (37)
- онстантин ћихайлов (“юмень) (49)
- онстантин ћихайлов (“юмень) часть 2 "–удра&a (12)
- космос (16)
- расота «емли (46)
- Ќаучные исследовани€ (186)
- ќ борьбе с паразитом за свою ¬олю (97)
- ќбсуждени€ тем из дневника "«вон –ун" (16)
- ѕереход (92)
- пирамиды (5)
- ѕорывы ƒуши (60)
- –уны –усского –ода (151)
- ћоЄ воспри€тие рун (19)
- рунна€ формула ѕерехода (5)
- –уны –усского –ода. ќсновы. (38)
- –усь (48)
- —ила звука, музыки и голоса (80)
- —ила —лова и –уский €зык (89)
- —каз как (116)
- от Jyj (13)
- огда поют руны ( от јсмик) (10)
- от ƒогоды (55)
- —ловарь –уского языка и примеры слогового разбора (21)
- —олнце и «емл€ (51)
- староверы, кержаки (31)
- —тихи ƒруга (64)
- ‘оменко ¬.Ќ. (27)
- футарк (17)
- ’осе јргуэльес (16)
- „еловеческий организм (209)
- ƒЌ (46)
- лечение (26)
- осознанные сновидени€ (13)
- позвоночник (15)
- эпифиз, шишковидна€ железа (13)
- Ёзотерика,религи€ (193)
- Ёкологи€ ћатери «емли (21)
-—сылки
-Ќовости
-ћузыка
- Mari Boine - Gula Gula
- —лушали: 1070 омментарии: 4
- “рек Jennifer Warnes & Bill Medley Ц The Time Of My Life (из к/ф √р€зные танцы)
- —лушали: 5945 омментарии: 0
- Bryan Adams & Barbara Streisand - I Finally Found Someone
- —лушали: 10074 омментарии: 0
- George Skaroulis "ќткуда в тебе столько нежности"
- —лушали: 13849 омментарии: 0
- «емфира - ∆ить в твоей голове
- —лушали: 605 омментарии: 4
-¬сегда под рукой
-ѕоиск по дневнику
-ѕодписка по e-mail
-—татистика
—оздан: 12.12.2012
«аписей: 1661
омментариев: 2966
Ќаписано: 6569
«аписей: 1661
омментариев: 2966
Ќаписано: 6569
»нформаци€ в голографической ¬селенной |
÷итата сообщени€ izzida

 Ёто навело мен€ в 1972 г. на мысль, что энтропи€ черной дыры пропорциональна площади поверхности ее горизонта событий. я предположил, что при падении вещества в черную дыру возрастание ее энтропии компенсирует или превосходит «потерю» энтропии вещества. —умма энтропии черной дыры и обычной энтропии вне ее не может уменьшатьс€. “аков обобщенный второй закон (ќ¬«) термодинамики. огда звезда коллапсирует, превраща€сь в черную дыру, энтропи€ дыры оказываетс€ гораздо больше энтропии звезды. ¬ 1974 г. ’окинг показал, что черна€ дыра спонтанно испускает тепловое излучение, известное сегодн€ как излучение ’окинга.
Ёто навело мен€ в 1972 г. на мысль, что энтропи€ черной дыры пропорциональна площади поверхности ее горизонта событий. я предположил, что при падении вещества в черную дыру возрастание ее энтропии компенсирует или превосходит «потерю» энтропии вещества. —умма энтропии черной дыры и обычной энтропии вне ее не может уменьшатьс€. “аков обобщенный второй закон (ќ¬«) термодинамики. огда звезда коллапсирует, превраща€сь в черную дыру, энтропи€ дыры оказываетс€ гораздо больше энтропии звезды. ¬ 1974 г. ’окинг показал, что черна€ дыра спонтанно испускает тепловое излучение, известное сегодн€ как излучение ’окинга.
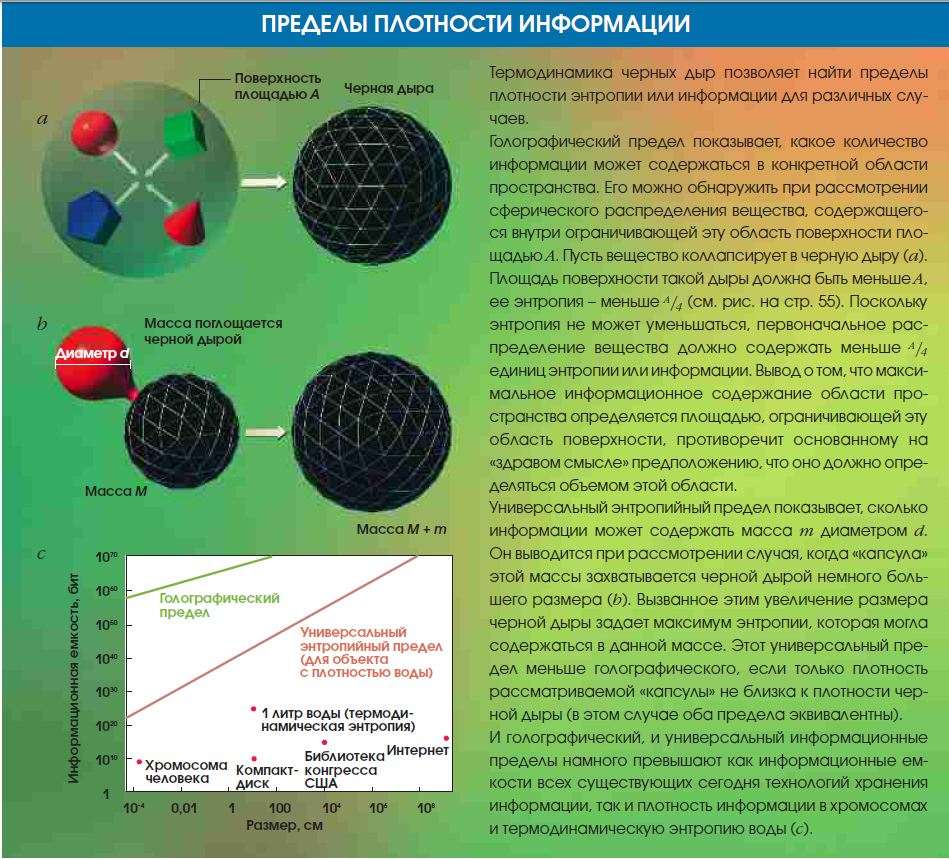 ” голографического предела есть и другой аспект: максимум возможной энтропии определ€етс€ площадью границы, а не заключенным в ней объемом.
” голографического предела есть и другой аспект: максимум возможной энтропии определ€етс€ площадью границы, а не заключенным в ней объемом.


 ƒопускает его и теори€ суперструн. √олографи€ же ограничивает число степеней свободы, которые могут существовать внутри граничной поверхности, конечным значением. “еори€ пол€ с ее бесконечностью не может быть последним словом.
ƒопускает его и теори€ суперструн. √олографи€ же ограничивает число степеней свободы, которые могут существовать внутри граничной поверхности, конечным значением. “еори€ пол€ с ее бесконечностью не может быть последним словом.

Ќа вопрос «из чего состоит физический мир» вам скорее всего ответ€т – «из вещества и энергии».
ќднако образованный человек непременно упом€нет и об информации, котора€ играет ключевую роль в живой и даже неживой природе. —огласно же теории ƒжона ”илера из ѕринстонского университета, физический мир состоит именно из информации, а вещество и энерги€ играют в нем второстепенную роль.
“ака€ точка зрени€ заставл€ет по новому взгл€нуть на старые проблемы. »нформационна€ емкость различных устройств, таких как дисковые накопители, растет очень быстро. огда этот процесс остановитс€? аков предел информационной емкости прибора массой, скажем, в один грамм и объемом не более кубического сантиметра (размер микросхемы)? акое количество информации необходимо дл€ полного описани€ ¬селенной? ћожет ли оно уместитьс€ в пам€ти компьютера? ћожем ли мы, как писал когда-то ”иль€м Ѕлейк (Whilliam Blake), «увидеть мир в песчинке» или это лишь поэтический образ?
Ќовейшие успехи теоретической физики дают ответы на некоторые из этих вопросов и помогают создавать теорию реальности. »зуча€ таинственные свойства черных дыр, физики вывели абсолютный предел объема информации, которую может хранить данна€ область пространства или данные количества вещества и энергии. –езультаты исследований заставл€ют задуматьс€ о том, что наша ¬селенна€, воспринимаема€ нами как трехмерна€, в действительности может быть «написана» на двухмерной поверхности подобно голограмме. ѕри этом наше воспри€тие мира как трехмерного может быть либо заблуждением, либо одним из альтернативных способов видени€ реальности. ѕесчинка не может заключать в себе весь наш мир, а плоский экран – может.
»стори€ двух энтропий
¬ основе формальной теории информации лежит разработка американского математика лода Ўеннона (Claud E. Shannon), опубликованна€ в 1948 г. ќн ввел наиболее употребительную меру информационного содержани€ – энтропию, котора€ долгое врем€ была центральным пон€тием термодинамики и которую обычно определ€ют как меру неупор€доченности физической системы. ¬ 1877 г. австрийский физик Ћюдвиг Ѕольцман определил энтропию как число различных микроскопических состо€ний, которые может принимать совокупность частиц, составл€юща€ некий «кусок» вещества, остава€сь на вид той же макроскопической «частью».
Ќапример, дл€ воздуха в комнате можно рассчитать все возможные пространственные распределени€ молекул и все их возможные движени€. ƒл€ описани€ способа количественного выражени€ информации, содержащейс€, например, в сообщении, Ўеннон предложил формулу, совпадающую с формулой Ѕольцмана. ѕо Ўеннону, энтропи€ сообщени€ – это число двоичных знаков, или битов, необходимое дл€ кодировани€ данной информации. Ёнтропи€ не отражает ценность сообщени€, котора€ полностью зависит от контекста, однако в качестве объективной меры количества информации она оказалась чрезвычайно полезной.
¬ частности, знание энтропии необходимо дл€ проектировани€ любого современного коммуникационного устройства – от сотового телефона до модема и проигрывател€ компакт-дисков. ¬ концептуальном отношении термодинамическа€ энтропи€ и энтропи€ Ўеннона эквивалентны: число распределений, подсчитываемое энтропией Ѕольцмана, отражает количество шенноновской информации, необходимое дл€ реализации любого конкретного распределени€. ќднако есть существенные различи€. ¬о-первых, энтропи€, которой пользуютс€ химики, выражаетс€ отношением энергии к температуре, а энтропи€ Ўеннона, используема€ специалистами по св€зи, – числом битов, т.е. величиной принципиально безразмерной. ќднако даже приведенные к одним и тем же единицам измерени€ численные значени€ этих величин будут различны. “ак, информационна€ энтропи€ микросхемы, хран€щей один гигабайт данных, составл€ет около 1010 бит (1 байт = 8 бит), а термодинамическа€ энтропи€ той же микросхемы при комнатной температуре имеет пор€док 10 23 бит.
–азличие объ€сн€етс€ тем, что они рассчитываютс€ дл€ различного числа степеней свободы (это люба€ величина, котора€ может измен€тьс€; например, координата, определ€юща€ положение частицы в пространстве.) Ёнтропи€ Ўеннона характеризует только состо€ние каждого из микроскопических транзисторов, сформированных в кристалле кремни€. “ранзистор может находитьс€ в одном из двух состо€ний – открытом или закрытом, которым соответствуют двоичные ноль и единица. «начит, он имеет одну двоичную степень свободы, в отличие от термодинамической энтропии, завис€щей от состо€ний миллиардов атомов (и их странствующих электронов), образующих транзистор. ѕо мере того, как миниатюризаци€ неуклонно приближает день, когда каждый атом сможет хранить один бит информации, численное значение полезной информационной энтропии микросхемы будет приближатьс€ к значению термодинамической энтропии материала, из которого она изготовлена. огда обе вычисл€ютс€ дл€ одинакового числа степеней свободы, они равны. аково предельное число степеней свободы? јтомы состо€т из электронов и €дер, €вл€ющихс€ скоплением протонов и нейтронов, которые, в свою очередь, состо€т из кварков.
ћногие физики считают электроны и кварки возбужденными состо€ни€ми суперструн, €вл€ющихс€ наиболее фундаментальными природными объектами. ќднако в структуре нашей ¬селенной может оказатьс€ больше уровней, чем полагает современна€ физика. „тобы рассчитать предельную информационную емкость некоего количества вещества или, что эквивалентно, его истинную термодинамическую энтропию, необходимо знать природу фундаментальных составл€ющих вещества или самого глубокого уровн€ его структуры, который € назову уровнем ’.
“ермодинамика черных дыр
—огласно уравнени€м общей теории относительности, разработанной јльбертом Ёйнштейном в 1915 г., достаточно больша€ концентраци€ вещества или энергии может искривить пространство-врем€ настолько, что оно разорветс€, образовав черную дыру. «аконы относительности не позвол€ют чему бы то ни было, попавшему внутрь нее, по€витьс€ вновь, по крайней мере, в рамках представлений классической (неквантовой) физики. ¬ажнейшее значение имеет рубеж невозврата, называемый горизонтом событий черной дыры. ¬ простейшем варианте он представл€ет собой сферу, радиус которой тем больше, чем больше масса черной дыры. ”знать, что находитс€ внутри нее, невозможно, т.к. никака€ информаци€ не может преодолеть этот горизонт. ќднако, исчеза€ навсегда, вещество оставл€ет некоторые следы: его энерги€ (в соответствии с уравнением Ёйнштейна E=mc2 мы считаем массу энергией) навсегда увеличивает ее массу.
≈сли перед захватом вещество обращалось вокруг черной дыры, его момент импульса добавл€етс€ к моменту импульса дыры. » массу, и момент импульса черной дыры можно определить по их вли€нию на пространство-врем€ в ее окрестности. “аким образом, законы сохранени€ энергии и импульса применимы к черной дыре. Ќо второй закон термодинамики, кажетс€, нарушаетс€. Ётот закон запрещает обратимые процессы, а значит, энтропи€ изолированной физической системы не может уменьшатьс€ – в лучшем случае она остаетс€ посто€нной, но обычно растет. Ётот закон – основа физической химии и техники. ак впервые отметил ”илер, когда вещество исчезает в черной дыре, его энтропи€ тоже пропадает навсегда, что представл€етс€ нарушением второго закона термодинамики. люч к этой разгадке по€вилс€ в 1970 г., когда аспирант ”илера в ѕринстонском университете ƒеметриус ’ристодулу и —тивен ’окинг из ембриджского университета независимо друг от друга доказали, что при сли€нии черных дыр обща€ площадь горизонта событий никогда не уменьшаетс€.
 Ёто навело мен€ в 1972 г. на мысль, что энтропи€ черной дыры пропорциональна площади поверхности ее горизонта событий. я предположил, что при падении вещества в черную дыру возрастание ее энтропии компенсирует или превосходит «потерю» энтропии вещества. —умма энтропии черной дыры и обычной энтропии вне ее не может уменьшатьс€. “аков обобщенный второй закон (ќ¬«) термодинамики. огда звезда коллапсирует, превраща€сь в черную дыру, энтропи€ дыры оказываетс€ гораздо больше энтропии звезды. ¬ 1974 г. ’окинг показал, что черна€ дыра спонтанно испускает тепловое излучение, известное сегодн€ как излучение ’окинга.
Ёто навело мен€ в 1972 г. на мысль, что энтропи€ черной дыры пропорциональна площади поверхности ее горизонта событий. я предположил, что при падении вещества в черную дыру возрастание ее энтропии компенсирует или превосходит «потерю» энтропии вещества. —умма энтропии черной дыры и обычной энтропии вне ее не может уменьшатьс€. “аков обобщенный второй закон (ќ¬«) термодинамики. огда звезда коллапсирует, превраща€сь в черную дыру, энтропи€ дыры оказываетс€ гораздо больше энтропии звезды. ¬ 1974 г. ’окинг показал, что черна€ дыра спонтанно испускает тепловое излучение, известное сегодн€ как излучение ’окинга.
Ёто €вление не согласуетс€ с теоремой ’ристодулу–’окинга (масса черной дыры и, следовательно, площадь ее горизонта уменьшаетс€), но ќ¬« разрешает противоречие: энтропи€ испускаемого излучени€ компенсирует уменьшение энтропии черной дыры, так что ќ¬« соблюдаетс€.
¬ 1986 г. –афаил —оркин сравнил роль горизонта событий черной дыры с барьером, не допускающим вли€ни€ информации, наход€щейс€ внутри дыры, на событи€ вне ее, чтобы показать, что ќ¬« должен соблюдатьс€ во всех процессах, касающихс€ черной дыры. ≈го глубокие рассуждени€ €сно показывают, что энтропи€ ќ¬« учитывает все уровни до ’ включительно, как бы глубоко тот ни лежал.
ѕроцесс излучени€ ’окинга позволил ему определить коэффициент пропорциональности между энтропией черной дыры и площадью горизонта событий: энтропи€ равна одной четверти площади горизонта, выраженной в планковских единицах (планковска€ единица площади – это квадрат длины ѕланка, фундаментальной константы, св€занной с т€готением и квантовой механикой, близкой к 10–33 см). Ёто огромна€ величина даже по термодинамическим представлени€м. Ёнтропи€ черной дыры диаметром 1 см составл€ет около 1066 бит, что примерно равно термодинамической энтропии вод€ного куба с ребром в 10 млрд. км.
ћир как голограмма
ќбобщенный второй закон термодинамики позвол€ет найти предел информационной емкости любой изолированной физической системы, т.е. предельный объем информации, котора€ может хранитьс€ на всех уровн€х ее структуры до уровн€ ’ включительно. ¬ 1980г. € начал изучать универсальный энтропийный предел, определ€ющий максимальный объем информации дл€ данной массы данного размера. —в€занный с ним голографический предел, устанавливающий максимальное значение энтропии, котора€ может содержатьс€ в веществе и энергии, занимающих данный объем пространства, был рассмотрен в 1995 г. Ћеонардом «ускиндом. ≈сли изолированна€ масса приблизительно сферической формы, не €вл€юща€с€ черной дырой и ограниченна€ замкнутой поверхностью с площадью A, коллапсирует, превраща€сь в черную дыру, то площадь ее горизонта событий станет меньше A.
—ледовательно, энтропи€ черной дыры будет меньше A/4. —огласно ќ¬«, энтропи€ не может уменьшатьс€, значит, первоначальна€ энтропи€ рассматриваемой массы не могла быть больше A/4. »з этого следует, что энтропи€ изолированной физической системы,
ограниченной поверхностью площади A, всегда меньше A/4. ј что если масса спонтанно не коллапсирует?
¬ 2000 г. € показал, что маленька€ черна€ дыра может быть использована дл€ превращени€ системы в черную дыру, мало чем отличающуюс€ от рассмотренной «ускиндом. “аким образом, предел за- висит только от ќ¬«, а не от строени€ системы или природы уровн€ ’. “еперь мы можем ответить на некоторые вопросы о пределах возможности хранени€ информации. ”стройство поперечником в 1 см может хранить до 1066 бит, в то врем€ как вс€ видима€ ¬селенна€ содержит не менее 10100 бит энтропии. Ёто количество может, в принципе, быть размещено в пределах сферы диаметром 0,1 светового года. Ќо оценка энтропии ¬селенной – трудна€ задача, дл€ решени€ которой понадоб€тс€ гораздо большие числа, требующие сферы размером с саму ¬селенную.
 ” голографического предела есть и другой аспект: максимум возможной энтропии определ€етс€ площадью границы, а не заключенным в ней объемом.
” голографического предела есть и другой аспект: максимум возможной энтропии определ€етс€ площадью границы, а не заключенным в ней объемом.
ѕредставим, что мы составл€ем большую систему из микросхем пам€ти. „исло транзисторов, определ€ющее информационную емкость, будет расти пропорционально ее объему.
“ак же будет возрастать и обща€ термодинамическа€ энтропи€ совокупности микросхем.
ѕримечательно, что теоретически предельна€ информационна€ емкость области пространства, занимаемой такой системой, будет увеличиватьс€ только пропорционально площади поверхности этой области. ѕоскольку объем растет быстрее площади поверхности, рано или поздно суммарна€ энтропи€ всех микросхем превысит голографический предел.
—оздаетс€ впечатление, что должны потерпеть крах либо наши представлени€ об энтропии и информационной емкости, либо ќ¬«.
Ќа самом деле построить такую систему невозможно: под действием внутренних гравитационных сил она сколлапсирует, превратитс€ в черную дыру, раньше, чем будет достигнут упом€нутый предел.

ѕосле этого кажда€ добавленна€ микросхема будет увеличивать массу и площадь поверхности черной дыры таким образом, что ќ¬« будет сохран€тьс€. ≈сли верен голографический принцип, предложенный в 1993 г. нобелевским лауреатом √ерардом ’офтом и развитый «ускиндом, то зависимость предела информационной емкости от площади поверхности, а не от объема вполне объ€снима. ¬ повседневной жизни голографи€ – это особый вид фотографии, позвол€ющий получать трехмерные изображени€ при использовании специального освещени€. ¬с€ информаци€ кодируетс€ в виде системы темных и светлых областей на двумерной поверхности фотопленки и всегда готова к воспроизведению.
√олографический принцип гласит, что подобным образом можно полностью описать любую физическую систему, занимающую некую область трехмерного пространства: он утверждает, что друга€ физическа€ теори€, определенна€ только дл€ двухмерной границы этой области, способна полностью описать физику ее трехмерного содержимого. ≈сли объемна€ система может быть полностью описана теорией, действующей только на двумерной границе этой системы, то можно ожидать, что информационное содержание системы не будет превышать аналогичного показател€ ее двумерной «оболочки».
¬селенна€, нарисованна€ на ее границе
ћожно ли применить голографический принцип ко всей ¬селенной? –еальна€ ¬селенна€ – это четырехмерна€ система, у которой есть объем, и она простираетс€ во времени. ≈сли ее физика голографична, должен существовать другой набор физических законов, действующих где-то на трехмерной границе четырехмерного пространства-времени. акую поверхность следует использовать в качестве границы ¬селенной?
ќдин из путей к осмыслению этих новых идей лежит в изучении моделей, более простых, чем реальна€ ¬селенна€. ѕримерами действи€ голографического принципа стали так называемые антидеситтеровские пространства-времена. »сходное пространство-врем€ де —иттера – это модель ¬селенной, впервые построенна€ в 1917 г. нидерландским астрономом ¬иллемом де —иттером как решение уравнений Ёйнштейна, включающее силу отталкивани€, называемую космологической посто€нной. ѕространство-врем€ де —иттера пусто, расшир€етс€ с ускорением и обладает высокой симметрией. ¬ 1997 г. астрономы, наблюдавшие взрывы далеких сверхновых, пришли к выводу, что расширение нашей ¬селенной ускор€етс€, и она, веро€тно, будет приближатьс€ к деситтеровскому пространству-времени. ≈сли в уравнени€х Ёйнштейна отталкивание заменить прит€жением, решение де —иттера окажетс€ антидеситтеровским пространством-временем, обладающим столь же высокой симметрией. роме того, это пространство-врем€ имеет границу, наход€щуюс€ на бесконечном удалении, и во многом оно подобно нашему привычному пространству-времени.
»спользу€ антидеситтеровское пространство-врем€, теоретики показали пример действи€ голографического принципа: ¬селенна€, описываема€ теорией суперструн, действующей в антидеситтеровском пространстве-времени, полностью эквивалентна квантовой теории пол€, действующей на границе этого пространства-времени. ѕервым предположение о таком соотношении дл€ п€тимерного антидеситтеровского случа€ высказал в 1997 г. ’уан ћалдасена. ¬последствии дл€ р€да случаев оно было подтверждено Ёдвардом ¬иттеном , а также —тивеном √абсером, »горем лебановым и јлександром ѕол€ковым.

—егодн€ примеры этого голографического соответстви€ известны дл€ пространств с различным числом измерений. “аким образом, две теории, казавшиес€ совершенно разными и даже действующими в пространствах с разным числом измерений, оказались эквивалентны. √олографическа€ эквивалентность, возможно, позволит нам заменить сложные вычислени€ таких €влений, как поведение кварков или глюонов в четырехмерном граничном пространстве-времени, более простыми вычислени€ми в высокосимметричном п€тимерном антидеситтеровском пространстве-времени. Ёто соответствие работает и в другом отношении. ”иттен показал, что черна€ дыра в антидеситтеровском пространстве-времени соответствует гор€чему излучению в альтернативной физике, действующей в граничном пространстве-времени. «агадочна€ энтропи€ черной дыры свелась к вполне пон€тной энтропии излучени€.
–асшир€юща€с€ ¬селенна€
¬ысокосимметрична€ и пуста€ п€тимерна€ антидеситтеровска€ ¬селенна€ мало похожа на нашу ¬селенную, существующую в четырехмерном пространстве-времени и заполненную веществом и энергией. ƒаже представив нашу реальную ¬селенную моделью, в которой вещество и излучение распределены равномерно, мы получим не антидеситтеровскую вселенную, а вселенную ‘ридмана––обертсона–”окера (‘–”). —егодн€ многие космологи согласны, что наша ¬селенна€ подобна вселенной ‘–”, котора€ бесконечна, не имеет границ и будет вечно расшир€тьс€. —огласуетс€ ли така€ ¬селенна€ с голографическим принципом или с голографическим пределом? –ассуждени€ «ускинда, основанные на рассмотрении коллапса с образованием черной дыры, не могут ответить на этот вопрос. ƒействительно, в однородной расшир€ющейс€ ¬селенной голографический предел, выведенный из анализа черных дыр, должен нарушатьс€.
Ёнтропи€ области, однородно заполненной веществом и излучением, действительно пропорциональна объему этой области, следовательно, при достаточно большом ее размере голографический предел неизбежно будет превышен. ¬ 1999 г. –афаил Ѕуссо, предложил модифицированный голографический предел, который, как оказалось, применим даже в тех случа€х, когда рассмотренные выше пределы неприменимы. Ѕуссо начинает с рассмотрени€ любой двумерной поверхности, котора€ может быть замкнутой, как сфера, или открытой, подобно листу бумаги. ѕредставьте себе короткую вспышку света, испускаемую одной стороной этой поверхности так, что лучи выход€т перпендикул€рно к ней в каждой точке. ≈динственное требование – изначальна€ сходимость лучей. “акому требованию отвечает, например, внутренн€€ поверхность сферической оболочки.
Ѕуссо рассматривает энтропию вещества и излучени€, через которые проход€т эти воображаемые лучи, в пределах до тех точек, где они начинают пересекатьс€. ќн предполагает, что эта энтропи€ не может быть больше энтропии рассматриваемой поверхности, т.е. больше четверти ее площади в планковских единицах. “акой подход к расчету энтропии отличен от примен€вшегос€ дл€ расчета первоначального голографического предела. ѕредел Ѕуссо характеризует не энтропию области в некоторый момент времени, а сумму энтропий отдельных подобластей в различные моменты времени – те, когда они «освещаютс€» вспышкой от поверхности. ѕредел Ѕуссо включает в себ€ другие пределы энтропии, но при этом он свободен от их недостатков. »з него можно вывести и универсальный энтропийный предел, и голографический предел ’офта–«ускинда дл€ любой не слишком быстро измен€ющейс€ изолированной системы с не слишком сильным гравитационным полем. огда вышеуказанные услови€ не действуют, например, при коллапсе шара из вещества, уже наход€щегос€ внутри черной дыры, эти пределы станов€тс€ неприменимыми, а предел Ѕуссо работает. ”ченый также показал, что такой подход можно использовать дл€ вы€влени€ двумерных поверхностей, на которых может быть «записана» голограмма мира.
ѕророки революции
”ченые предложили существование многих других пределов дл€ энтропии. Ќо хот€ голографический подход осмыслен еще не до конца, от него, видимо, уже невозможно отказатьс€, а господствовавшее 50 лет представление, будто теори€ пол€ €вл€етс€ последним словом физики, придетс€ пересмотреть. “акие пол€, как электромагнитное, измен€ютс€ от точки к точке непрерывным образом и, следовательно, допускают неограниченное число степеней свободы.
 ƒопускает его и теори€ суперструн. √олографи€ же ограничивает число степеней свободы, которые могут существовать внутри граничной поверхности, конечным значением. “еори€ пол€ с ее бесконечностью не может быть последним словом.
ƒопускает его и теори€ суперструн. √олографи€ же ограничивает число степеней свободы, которые могут существовать внутри граничной поверхности, конечным значением. “еори€ пол€ с ее бесконечностью не может быть последним словом.
Ѕолее того, даже если бесконечность удастс€ «приручить», придетс€ как-то оправдывать таинственную зависимость информации от площади поверхности.
“олчком к созданию более совершенной теории может оказатьс€ голографи€. акой должна быть фундаментальна€ теори€? ÷епь рассуждений, включающих в себ€ голографические представлени€, привела некоторых ученых, в частности Ћи —молина, к предположению, что така€ фундаментальна€ теори€ должна иметь дело не с пол€ми и даже не с пространством-временем, а с обменом информацией между физическими процессами.
≈сли это так, то видение информации как «материала», из которого построен мир, найдет достойное воплощение.
ќЅ ј¬“ќ–≈:
якоб Ѕекенштейн – €вл€етс€ одним из основателей термодинамики черных дыр и внес весомый вклад в изучение различных аспектов св€зи между информацией и т€готением.
—ери€ сообщений "космос":
„асть 1 - ќбнаружили Ђкосмические нитиї, св€зывающие объекты ¬селенной
„асть 2 - ћодель не ѕриродных объектов осмоса
...
„асть 10 - √рафик —олнечной активности за 2011 год
„асть 11 - √рафик —олнечной активности за 2012 год
„асть 12 - »нформаци€ в голографической ¬селенной
„асть 13 - ѕочему мы движемс€ так быстро и ”ƒј?
„асть 14 - ѕузыри ‘ерми
„асть 15 - ака€ красота! ќб€зательно посмотрите видео! —еверное си€ние с 12 на 13 сент€бр€
„асть 16 - ESO опубликовала видео "полЄта" к звЄздному скоплению " олодец ∆еланий"
| –убрики: | Ќаучные исследовани€ |
| омментировать | « ѕред. запись — дневнику — —лед. запись » | —траницы: [1] [Ќовые] |







